1.3.1. Счётные множества.

1. Любое бесконечное подмножество В счётного множества А также счётно.

        Элементы В можно перенумеровать в порядке их следования в А; так как В бесконечно, для нумерации будут использованы все натуральные числа.

2. Объединение конечной или счётной совокупности счётных множеств - счётное множество.

        Докажем последнее утверждение сначала для двух счётных множеств А={a₁, a₂, a₃,…} и В ={b₁, b₂, b₃,…}. Выпишем все элементы этих множеств в одну строчку a₁, b₁, a₂, b₂, a₃, b₃,… и сопоставим каждому элементу его номер в этой строчке (если A∩B ≠ , т.е. какой-то элемент входит и в А, и в В, он получает номер только в первый раз, а во второй раз пропускается). В результате будут пронумерованы все элементы множества A∪B, что доказывает его счётность. Также доказывается счётность объединения трёх, четырёх и вообще любого конечного числа счётных множеств. В случае счётного числа счётных множеств {A₁, A₂, A₃, A₄, …}способ нумерации может быть, например, таким: Нумерация начинается с элемента a₁₁ и продолжается в направлении стрелок, повторяющиеся элементы при этом пропускаются.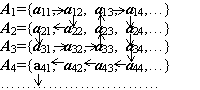

        3. Множество Q рациональных чисел счётно.         Множество рациональных чисел (чисел вида p/q, где p, q - целые числа, q ≠ 0) можно представить как объединение счётного числа следующих счётных множеств: множества Q₁ всех целых чисел n=0, 1, 2, 3,….; множество Q₂ всех дробей вида n/2, множество Q₃ всех дробей вида n/3,……………., множество Q_к всех дробей вида n/к, n=0, 1, 2, 3,…..; следовательно, оно счётно.

        Задание. Самостоятельно доказать следующие утверждения:         4. Если А = {a_n| n ∈ Z} и B = {B_n| n ∈ Z} - счётные множества, то множество всех пар {(a_n, b_к)| n, к ∈ Z} - счётно.         5. Множество всех многочленов P(x) = a₀ + a₁·x + a₂·x² + a₃·x³ + … +a_n·xⁿ (произвольных степеней) с рациональными коэффициентами (a_i ∈ Q) счётно.         6. Алгебраическим числом называется число, которое может быть корнем многочлена с рациональными коэффициентами. Доказать, что множество алгебраических чисел счётно.         7. Множество всех отрезков [a,b] с рациональными концами a, b счётно.         8. Множество взаимно не пересекающихся интервалов (a, b) на оси счётно.         9. Множество точек разрыва монотонной функции счётно.

1.3.2. Множества мощности континуум.

        1. Множество мощности континуум несчётно.         Док-во. Применим метод доказательства от противного. Множество мощности континуум - множество, равномощное множеству точек любого отрезка. Возьмём отрезок [0,1]. Каждой точке х ∈ [0,1] сопоставим представление числа х в виде бесконечной десятичной дроби вида х = α₀, α₁α₂α₃ …..; это представление единственно, если договориться, что в случаях возможной неоднозначности (число 0,5, например, можно представить и в виде 0,5000000…., и в виде 0,4999999….) применяется представление c периодом, равным нулю. Предположим, что множество точек, а следовательно, и множество таких дробей счётно, т.е. они могут быть пронумерованы, в качестве номера используем верхний индекс:

х(1) = α0(1),α1(1) α2(1)α3(1)…….; х(2) = α 0(2),α1(2) α2(2)α3(2)…….; х(3) = α 0(3),α1(3) α2(3)α3(3)…….; ……………………………...; х (n) = α0(n),α 1(n)α2(n) α3(n)…….; ……………………………….

Построим точку х = β0,β1 β2β3….. ∈ [0,1], заведомо не принадлежащую этой последовательности. Возьмём β0 = 0. В качестве β1 возьмём любую цифру, неравную α1(1) и 9; в качестве β2 - любую цифру, неравную α 2(2) и 9 и т.д.; вообще в качестве βn возьмём любую цифру, неравную αn(n) и 9. Построенная точка не может входить в последовательность х(1), х(2), х(3),…, х(n),…, (х ≠ х(n), т.к. β(n) ≠ αn(n)) - получено противоречие с предположением о счётности точек отрезка.

        2. Если А - бесконечное множество, В - конечное или счётное множество, то A∪B - множество, равномощное А.         Выберем в А счётное подмножество С и пусть D = А\С. Тогда А = D∪С; A∪В = D∪(С∪В). С и В - счётные множества, следовательно, С∪В -также счётное множество, т.е. существует взаимно-однозначное соответствие между элементами С и С∪В. Применяя это соответствие и тождественное соответствие между элементами множества D, получим взаимно-однозначное соответствие между элементами D∪С и D∪(С∪B), что означает равномощность множеств А и А∪В.         Следует отметить, что из этого свойства непосредственно следует равномощность множеств точек отрезка и интервала.

        Задание. Самостоятельно доказать следующие утверждения:         3. Множество иррациональных чисел имеет мощность континуум.         4. Число, не являющееся алгебраическим, называется трансцендентным. Доказать, что множество трансцендентных чисел имеет мощность континуум.