
- •1. Элементы теории множеств.
- •1.1. Множества, подмножества, элементы множества.
- •1.2. Операции над множествами.
- •Свойства операции объединения.
- •Свойства операции пересечения множеств.
- •1.3.1. Счётные множества.
- •1.3.2. Множества мощности континуум.
- •1.3.3. Множества высших мощностей.
- •2. Элементы математической логики.
- •2.1. Высказывания и действия над ними.
- •Свойства логических операций.
- •2. Элементы математической логики.
- •2.2. Кванторы.
- •2.3. Математические теоремы, их виды и логическая структура.
- •2.3.1. Теоремы прямая, противоположная, обратная.
- •2.3.2. Достаточность и необходимость, существование и единственность.
- •2.3.3. Доказательство от противного; метод математической индукции .
- •2.3.4. Бином Ньютона.
- •3. Действительные числа.
- •3.1. Аксиомы действительных чисел.
- •3.2. Некоторые множества на числовой оси.
- •3.3. Несобственные точки числовой прямой.
- •3.4. Границы числовых множест.
- •5.4. Односторонняя непрерывность. Классификация точек разрыва.
- •5.6. Свойства функций, непрерывных на отрезке.
2.3.4. Бином Ньютона.
Набор элементов {ak1, ak2, ak3, ..., akm}, (всего m элементов), выбранных без повторения из множества {a1, a2, a3, …, an}, содержащего n элементов, где m ≤ n, называется выборкой объема m из n элементов. Пусть, например, даны выборки {a1, a4}, {a2, a3, a4}, {a3, a2, a4}; все приведенные выборки разные: первые две отличаются количеством элементов, последние две выборки отличаются порядком элементов. Выборки {ak1, ak2, ak3, ..., akm}, в которых учитывается не только набор элементов, но и их порядок, называются размещениями. Число различных возможных размещений из n элементов множества по m (m - объем выборки) обозначается символом Anm. Имеет место формула
![]() Доказательство:
если все множество содержит n
элементов, то имеется ровно n
вариантов выбора одного элемента; при
любом выборе первого элемента вариантов
выбора второго элемента будет n
- 1; следовательно, вариантов выбора двух
элементов будет n(n
- 1); вариантов выбора третьего элемента
из оставшихся n
- 2 элементов будет тоже n
- 2; следовательно, три элемента можно
выбрать n(n
- 1)(n
- 2) способами; таким образом, для любого
числа m,
m
≤ n,
получаем
Доказательство:
если все множество содержит n
элементов, то имеется ровно n
вариантов выбора одного элемента; при
любом выборе первого элемента вариантов
выбора второго элемента будет n
- 1; следовательно, вариантов выбора двух
элементов будет n(n
- 1); вариантов выбора третьего элемента
из оставшихся n
- 2 элементов будет тоже n
- 2; следовательно, три элемента можно
выбрать n(n
- 1)(n
- 2) способами; таким образом, для любого
числа m,
m
≤ n,
получаем
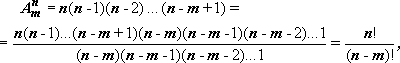 где
n!
= 1·2·3…·n;
при этом по определению полагается 1! =
1, 0! = 1.
Выборки,
для которых m
= n,
называются перестановками. Например,
{a1,
a2,
a3},
{a2,
a3,
a1},
{a3,
a1,
a2}
и т.д. Число перестановок из n
элементов обозначается символом Pn,
так как Pn
= Pnn
= n(n
- 1)(n
- 2) ... (n
- n
+ 1), то Pn
= n!
Если
учитывается только набор элементов в
выборке (независимо от их порядка), то
такие выборки называются сочетаниями.
Пусть, например, имеются выборки {a1,
a2,
a3},
{a2,
a3,
a1},
{a3,
a6,
a2};
первые две из них получаются друг из
друга перестановкой элементов, поэтому
как сочетания они не различаются (но
различаются как перестановки); две
последние выборки содержат разные
наборы элементов, поэтому как сочетания
они разные. Число сочетаний из n
элементов по m
обозначим Cnm.
Если набор содержит n
элементов, то из этих элементов можно
сделать Anm
размещений, при этом каждому размещению
соответствует еще Pn
- 1 размещение, отличающееся от него
только порядком элементов, т.е.
тождественные с ним как сочетания.
Поэтому Anm
= Cnm
· Pm,
то есть
где
n!
= 1·2·3…·n;
при этом по определению полагается 1! =
1, 0! = 1.
Выборки,
для которых m
= n,
называются перестановками. Например,
{a1,
a2,
a3},
{a2,
a3,
a1},
{a3,
a1,
a2}
и т.д. Число перестановок из n
элементов обозначается символом Pn,
так как Pn
= Pnn
= n(n
- 1)(n
- 2) ... (n
- n
+ 1), то Pn
= n!
Если
учитывается только набор элементов в
выборке (независимо от их порядка), то
такие выборки называются сочетаниями.
Пусть, например, имеются выборки {a1,
a2,
a3},
{a2,
a3,
a1},
{a3,
a6,
a2};
первые две из них получаются друг из
друга перестановкой элементов, поэтому
как сочетания они не различаются (но
различаются как перестановки); две
последние выборки содержат разные
наборы элементов, поэтому как сочетания
они разные. Число сочетаний из n
элементов по m
обозначим Cnm.
Если набор содержит n
элементов, то из этих элементов можно
сделать Anm
размещений, при этом каждому размещению
соответствует еще Pn
- 1 размещение, отличающееся от него
только порядком элементов, т.е.
тождественные с ним как сочетания.
Поэтому Anm
= Cnm
· Pm,
то есть
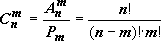 .
Частные
случаи: если m
= 0, то
.
Частные
случаи: если m
= 0, то
![]() ;
если m
= 1, то
;
если m
= 1, то
![]() ;
если если m
= 2, то
;
если если m
= 2, то
![]() ;
… если m
= n
- 1, то
;
… если m
= n
- 1, то
![]() ;
если m
= n,
то
;
если m
= n,
то
![]() .
.
Биномом Ньютона называют разложение выражения (a ± b)n по степеням a и b (n - натуральное число).
Количество
слагаемых в многочлене (a
± b)n
до приведения подобных членов при
увеличении показателя степени на единицу
увеличивается в два раза (поэтому общее
количество слагаемых до приведения
подобных членов будет равно 2n
+ 1).
Когда приводятся подобные члены в
многочлене (a
± b)n,
то определяются по сути количества
одинаковых слагаемых, то есть числа
сочетаний из n
элементов по m
(ясно, что
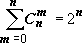 ).
До сложения
показателей слагаемые в разложении
бинома (a
± b)n
имеют вид: a·a·a·
… a·(±b)·(±b)·(±b)·
… (±b);
каждое слагаемое содержит n
множителей. Количество слагаемых,
которые содержат множитель (±b)
m
раз совпадает с количеством сочетаний
по m
из n
элементов; такие слагаемые будут иметь
вид (±b)m·an
- m;
общее число таких слагаемых равно Cnm,
что приводит к так называемой формуле
бинома Ньютона:
).
До сложения
показателей слагаемые в разложении
бинома (a
± b)n
имеют вид: a·a·a·
… a·(±b)·(±b)·(±b)·
… (±b);
каждое слагаемое содержит n
множителей. Количество слагаемых,
которые содержат множитель (±b)
m
раз совпадает с количеством сочетаний
по m
из n
элементов; такие слагаемые будут иметь
вид (±b)m·an
- m;
общее число таких слагаемых равно Cnm,
что приводит к так называемой формуле
бинома Ньютона:
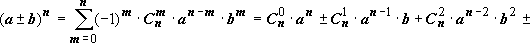
![]()
![]() Для
наглядного представления значений
биномиальных коэффициентов Cnm
применяют таблицу, называемую треугольником
Паскаля:
Для
наглядного представления значений
биномиальных коэффициентов Cnm
применяют таблицу, называемую треугольником
Паскаля:
 Каждый
внутренний элемент этой таблицы
получается как сумма элементов, стоящих
левее и правее строкой выше.
Рассмотрим
некоторые свойства биномиальных
коэффициентов, которые хорошо
просматриваются в треугольнике Паскаля:
а).
Свойство, используемое при построении
треугольника Паскаля:
Cn+1k+1
= Cnk
+ Cnk+1.
б).
Число элементов в строке (в разложении
бинома степени n) на единицу больше
показателя степени бинома.
в).
Сумма биномиальных коэффициентов в
любой строке равна 2n,
то есть
Каждый
внутренний элемент этой таблицы
получается как сумма элементов, стоящих
левее и правее строкой выше.
Рассмотрим
некоторые свойства биномиальных
коэффициентов, которые хорошо
просматриваются в треугольнике Паскаля:
а).
Свойство, используемое при построении
треугольника Паскаля:
Cn+1k+1
= Cnk
+ Cnk+1.
б).
Число элементов в строке (в разложении
бинома степени n) на единицу больше
показателя степени бинома.
в).
Сумма биномиальных коэффициентов в
любой строке равна 2n,
то есть
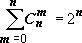 .
г).
Cnm
= Сnn-m,
так как
.
г).
Cnm
= Сnn-m,
так как
![]() .
Это свойство
означает, что таблица Паскаля симметрична
относительно своей центральной линии,
или, другими словами, равноотстоящие
от краев элементы строки одинаковы:
нулевой элемент равен последнему (Cn0
= Cnn
= 1, m
= 0); первый элемент равен предпоследнему
(Cn1
= Cnn
- 1
= n,
m
= 1); и т.д.
д).
Сумма биномиальных коэффициентов,
стоящих на четных местах, равна сумме
биномиальных коэффициентов, стоящих
на нечетныx местах.
е).Каждый
элемент строки равен предшествующему,
умноженному на коэффициент, равный
.
Это свойство
означает, что таблица Паскаля симметрична
относительно своей центральной линии,
или, другими словами, равноотстоящие
от краев элементы строки одинаковы:
нулевой элемент равен последнему (Cn0
= Cnn
= 1, m
= 0); первый элемент равен предпоследнему
(Cn1
= Cnn
- 1
= n,
m
= 1); и т.д.
д).
Сумма биномиальных коэффициентов,
стоящих на четных местах, равна сумме
биномиальных коэффициентов, стоящих
на нечетныx местах.
е).Каждый
элемент строки равен предшествующему,
умноженному на коэффициент, равный
![]() ,
то есть
,
то есть
![]() .
В самом деле,
.
В самом деле,
![]() .
.
