
- •1. Основні означення та необхідні відомості з теорії груп та кілець
- •2. Кільця лишків за модулем m
- •3. Кільця поліномів
- •3.1. Поліноми над кільцями
- •3.2. Поліноми над полями
- •3.3. Фактор-кільце f[X]/(f)
- •4. Корені поліномів та їх властивості
- •5. Поля часток
- •Підполя. Прості поля. Характеристики полів
- •Розширення полів
- •Алгебраїчні розширення
- •9. Мінімальні поліноми
- •Прості розширення полів та їх побудова
- •Поля розкладу поліномів
- •12. Теорема про існування та єдиність скінченних полів
- •13. Критерій підполя, діаграми включення підполів
- •14. Мультиплікативна група скінченного поля
- •Наслідки теореми 30.
- •15. Незвідні поліноми та їх корені
- •16. Спряжені елементи
- •17. Зображення елементів скінченних полів
- •18. Порядки поліномів
- •19. Примітивні поліноми
- •20. Сліди та норми
- •21. Базиси
- •22. Автоморфізми скінченних полів
- •23. Зведення основних положень та результатів
- •Предметний покажчик
- •Список використаної літератури
9. Мінімальні поліноми
Нехай
![]() – алгебраїчний над F
елемент
розширення
– алгебраїчний над F
елемент
розширення
![]() ,
причому
,
причому
![]() .
Нескладно показати, що множина
.
Нескладно показати, що множина
![]() є ідеалом кільця
є ідеалом кільця
![]() ,
причому
,
причому
![]() ,
так як
,
так як
![]() –
алгебраїчний елемент.
Оскільки
–
алгебраїчний елемент.
Оскільки
![]() – кільце головних ідеалів, то
– кільце головних ідеалів, то
![]() ,
де g
–
нормований поліном над F
найменшого
степеня серед ненульових поліномів, що
належать J.
Доведемо
незвідність g.
Оскільки
,
де g
–
нормований поліном над F
найменшого
степеня серед ненульових поліномів, що
належать J.
Доведемо
незвідність g.
Оскільки
![]() ,
то
,
то
![]() ,таким
чином,
,таким
чином,
![]() .Припустимо,
що поліном g
–
звідний. Тоді
.Припустимо,
що поліном g
–
звідний. Тоді
![]() ;
;
![]()
![]() або
або
![]() або
або
![]() .
Так як
.
Так як
![]() ,
то це входить у протиріччя з мінімальністю
степеня
,
то це входить у протиріччя з мінімальністю
степеня
![]() у
у
![]() .
.
Поліном
g,
що породжує ідеал
![]() називається мінімальним
поліномом елемента
.
називається мінімальним
поліномом елемента
.
Вище
був розглянутий випадок
![]() .
Для
.
Для
![]() мінімальним буде поліном
мінімальним буде поліном
![]() .
.
Отже,
кожний алгебраїчний елемент розширення
![]() має мінімальний поліном над F.
має мінімальний поліном над F.
Степінь мінімального полінома елемента називається степенем цього елемента.
Вищенаведені міркування повністю доводять наступну теорему.
ТЕОРЕМА
22.
Нехай
![]() –
розширення поля F,
елемент
–
розширення поля F,
елемент
![]() – алгебраїчний над F.
Тоді
має мінімальний поліном
– алгебраїчний над F.
Тоді
має мінімальний поліном
![]() ,
причому:
,
причому:
-
g – незвідний поліном;
-
 ;
; -
g є нормованим поліномом мінімального степеня, для якого є коренем.
ТЕОРЕМА
23.
Нехай
![]() –
розширення поля F,
елемент
–
розширення поля F,
елемент
![]() – алгебраїчний над F,
g
–
мінімальний поліном для ,
– алгебраїчний над F,
g
–
мінімальний поліном для ,
![]() .
Тоді:
.
Тоді:
-
 ;
; -
 – лінійний
векторний простір над F
розмірності
n,
і
– лінійний
векторний простір над F
розмірності
n,
і
 – його базис;
– його базис; -
будь-який елемент
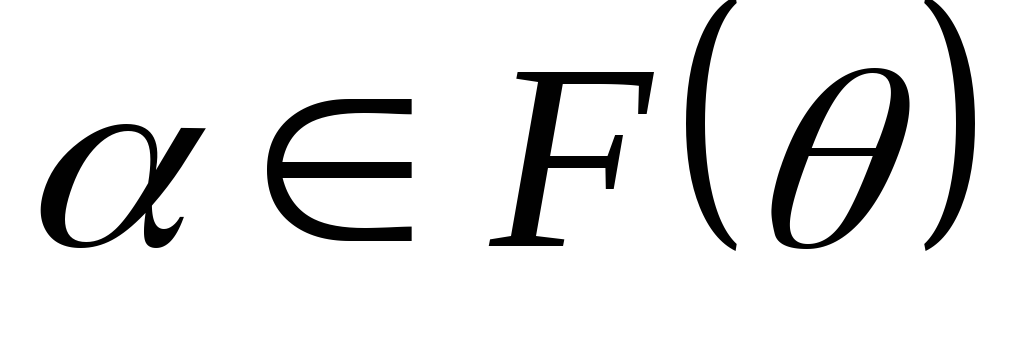 є алгебраїчним над F,
причому степінь
є алгебраїчним над F,
причому степінь
 ділить
n.
ділить
n.
1)
Розглянемо відображення
![]() ,
визначене як
,
визначене як
![]() .
.
Тоді
![]() .
Очевидно, що –
гомоморфізм. За теоремою
про гомоморфізм кілець
.
Очевидно, що –
гомоморфізм. За теоремою
про гомоморфізм кілець
![]() .
.
![]() ,
тобто
,
тобто
![]() .
Залишилося довести, що
.
Залишилося довести, що
![]() .
Оскільки
.
Оскільки
![]() незвідний,
то
незвідний,
то
![]() - поле,
отже і
- поле,
отже і
![]() -
поле. входить
в S,
оскільки
-
поле. входить
в S,
оскільки
![]() .
Але оскільки F
і
входять
в S,
а F(
.
Але оскільки F
і
входять
в S,
а F(![]() )
– мінімальне поле, що містить F
і
,
то
)
– мінімальне поле, що містить F
і
,
то
![]() .
.
2)
Доведемо, що
![]() .
Маємо:
.
Маємо:![]()
![]() ,
,![]() ,
але
,
але
![]() за умовою, тому,
за умовою, тому,
![]() де
де
![]() завжди можна представити у вигляді
завжди можна представити у вигляді
![]() .
Залишилося показати, що
.
Залишилося показати, що
![]() – лінійно незалежна система:
– лінійно незалежна система:
![]()
![]()
![]() ,
але
,
але
![]() ,
а
,
а
![]() -
поліном
найменшого степеня в
-
поліном
найменшого степеня в
![]() .
Отже, залишається лише одна можливість:
.
Отже, залишається лише одна можливість:
![]() ,
тобто
,
тобто
![]() .
.
3)
Оскільки F(θ)
– скінченне розширення (доведено в
п.2), то воно алгебраїчне (див. теор.21).
Отже, будь-який його елемент алгебраїчний
над F
(за означенням), тобто
![]() –
алгебраїчний над F.
За теор.20
–
алгебраїчний над F.
За теор.20
![]()
![]()
![]() .
.
Надалі, якщо не обумовлене протилежне, розглядатимемо тільки скінченні поля.
-
Прості розширення полів та їх побудова
До цього
ми будували розширення поля F,
приєднуючи до нього елементи деякого
ширшого поля
![]() .
Спробуємо тепер побудувати розширення
F,
не маючи ширшого поля. Необхідний
результат дає наступна теорема.
.
Спробуємо тепер побудувати розширення
F,
не маючи ширшого поля. Необхідний
результат дає наступна теорема.
ТЕОРЕМА
24.
Нехай
F[x]
– кільце поліномів над полем F,
![]() – незвідний поліном. Тоді фактор-кільце
– незвідний поліном. Тоді фактор-кільце
![]() ізоморфне деякому простому розширенню
поля F.
ізоморфне деякому простому розширенню
поля F.
За
теор.10
![]() – поле. Його елементами є класи лишків
– поле. Його елементами є класи лишків
![]()
![]() ,
,
![]() .
Операції на класах лишків вводяться
звичайним способом:
.
Операції на класах лишків вводяться
звичайним способом:
![]() ,
, ![]() .
.
Розглянемо
множину класів лишків виду
![]()
![]() ,
,
![]() .
Класи
.
Класи
![]() і
і
![]() при
при
![]() не перетинаються. Таким чином, кожному
елементу
поля
не перетинаються. Таким чином, кожному
елементу
поля
![]() можна
співставити елемент
можна
співставити елемент
![]() поля
поля
![]() ,
і це відображення є ізоморфізмом. Отже,
елементи вигляду
,
і це відображення є ізоморфізмом. Отже,
елементи вигляду
![]() можна ототожнити з елементами
можна ототожнити з елементами
![]() ,
і
,
і
![]() дійсно
є розширенням
дійсно
є розширенням
![]()
Покажемо, що g має корінь в одержаному розширенні і цим коренем є елемент [x]. Згідно з введеними операціями на класах лишків

(елементи
![]() можна
розглядати як елементи розширення
можна
розглядати як елементи розширення
![]() ).
).
Кожен
елемент
![]()
![]() ,
,
![]() може бути представлений у вигляді
може бути представлений у вигляді
![]() ,
і
,
і
![]() містить всі елементи такого виду. Але
поле, одержане шляхом приєднання
елемента
містить всі елементи такого виду. Але
поле, одержане шляхом приєднання
елемента
![]() ,
якраз і повинно складатися з усіх
елементів такого виду. Отже,
,
якраз і повинно складатися з усіх
елементів такого виду. Отже,
![]() співпадає з простим алгебраїчним
розширенням
співпадає з простим алгебраїчним
розширенням
![]() з точністю до ізоморфізму.
з точністю до ізоморфізму.
Тепер стає очевидною
ТЕОРЕМА
25.
Для
будь-якого незвідного полінома
![]() існує з точністю до ізоморфізму розширення
поля F,
в якому f
має
хоча б один корінь.
існує з точністю до ізоморфізму розширення
поля F,
в якому f
має
хоча б один корінь.
Теорема
24
є переформулюванням п.1
теор.23,
але в ній не передбачається існування
розширення
![]() і алгебраїчного над F
елемента
і алгебраїчного над F
елемента
![]() .
Завдяки теор.24
можна
розширювати скінченні поля, починаючи
з простих, адже будова останніх нам
відома –
це не що інше, як кільця лишків за простим
модулем Zp
з операціями за модулем
.
Завдяки теор.24
можна
розширювати скінченні поля, починаючи
з простих, адже будова останніх нам
відома –
це не що інше, як кільця лишків за простим
модулем Zp
з операціями за модулем
![]() .
Отже, з них можна будувати більш складні
(розширені) скінченні поля, будуючи
фактор-кільця
.
Отже, з них можна будувати більш складні
(розширені) скінченні поля, будуючи
фактор-кільця
![]() так, як описано у п.3.3.
Щоправда, для цього потрібно мати
незвідний над F
поліном. Існування незвідних поліномів
будь-якого степеня над заданим скінченним
полем буде доведено нижче (див. наслідок
4 з
теор.30).
так, як описано у п.3.3.
Щоправда, для цього потрібно мати
незвідний над F
поліном. Існування незвідних поліномів
будь-якого степеня над заданим скінченним
полем буде доведено нижче (див. наслідок
4 з
теор.30).
Приклад.
Розглянемо
поліном
![]() над полем
F5.
В F5
він
не має коренів. За теор.24
у
фактор-кільці F5
над полем
F5.
В F5
він
не має коренів. За теор.24
у
фактор-кільці F5![]() ,
яке через незвідність
,
яке через незвідність![]() буде полем, поліном
буде полем, поліном
![]() має корінь
має корінь F5
F5![]() .
Виходячи з того, що степінь кожного
полінома, що представляє елемент поля
F5
.
Виходячи з того, що степінь кожного
полінома, що представляє елемент поля
F5![]() ,
повинен
бути меншим за степінь g(x)
(представниками класів лишків є лишки
від ділення на g),
робимо висновок, що всі його елементи
можна зобразити у вигляді
,
повинен
бути меншим за степінь g(x)
(представниками класів лишків є лишки
від ділення на g),
робимо висновок, що всі його елементи
можна зобразити у вигляді
![]()
![]() .
.
Корінь
![]() можна позначати по-різному. Наприклад,
враховуючи, що
можна позначати по-різному. Наприклад,
враховуючи, що
![]() ,
можемо записати:
,
можемо записати:
![]() . Введемо операції:
. Введемо операції:
![]() ,
,
![]() Таким
чином одержуємо просте розширення F5
(
Таким
чином одержуємо просте розширення F5
(![]() ).
).
ТЕОРЕМА
26.
Нехай F
–
поле,
![]() – незвідний поліном,
– незвідний поліном,
![]() ,
–
його корені. Тоді прості розширення
,
–
його корені. Тоді прості розширення
![]() і
і
![]() ізоморфні.
ізоморфні.
Це очевидно випливає з теор.24 і транзитивності відношення ізоморфності:
![]()
![]() F[x]/(f)
F[x]/(f)![]() .
.
Контрольні питання до §9,10
-
Дати визначення мінімального поліному, незвідного полніому.
-
Сформулювати теорему про властивості мінімального поліному.
-
Яке розширення поля називається простим?
Задачі до §9,10
-
Нехай К – підполе поля F, ΘF. Довести:
 ,
де g
– мінімальний поліном
елементу
Θ.
,
де g
– мінімальний поліном
елементу
Θ. -
Чи є справедливим твердження:

 є коренями одного й того ж незвідного
поліному над К?
є коренями одного й того ж незвідного
поліному над К? -
Довести, що
 - незвідний; побудувати таблиці операцій
для простого розширення F2(Θ),
де Θ – корінь
вказанного поліному.
- незвідний; побудувати таблиці операцій
для простого розширення F2(Θ),
де Θ – корінь
вказанного поліному. -
Нехай К – поле. Довести: f,gK[x] мають спільний корінь (з деякого розширення К)
 .
. -
Довести: будь-яке поле характеристики р ізоморфне
 .
. -
Довести: при
 поліном
поліном
 ділится на
ділится на
 в
в
 .
. -
Нехай F – скінченне поле. Довести: char F=ord e в адитивній групі цього поля.
-
Нехай
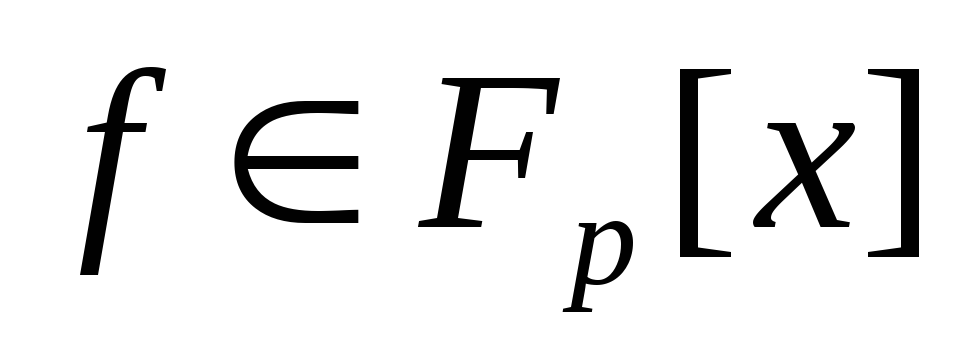 .
Чи є справедливим твердження:
f
– простий
(f)
– простий?
.
Чи є справедливим твердження:
f
– простий
(f)
– простий? -
Нехай F – поле,
 .
Довести: pa=0
pb=0,
де p
– просте число. Чи є справедливим дане
твердження для кільця?
.
Довести: pa=0
pb=0,
де p
– просте число. Чи є справедливим дане
твердження для кільця? -
Довести: незвідний поліном не має кратних коренів.
-
Нехай F – скінчене поле, К F – підкільце. Довести: К – підполе.
-
Довести: якщо n – просте, то
 не має інших підполів,
крім простого. Яке це підполе?
не має інших підполів,
крім простого. Яке це підполе? -
Нехай f, g K[x]. Довести: f, g мають спільний корінь хоча б один з них звідний.
-
Довести:
 незвідний над F2
t
непарне.
незвідний над F2
t
непарне. -
Нехай
 .
Який
степінь
мінімального
поліному
елемента
над
.
Який
степінь
мінімального
поліному
елемента
над
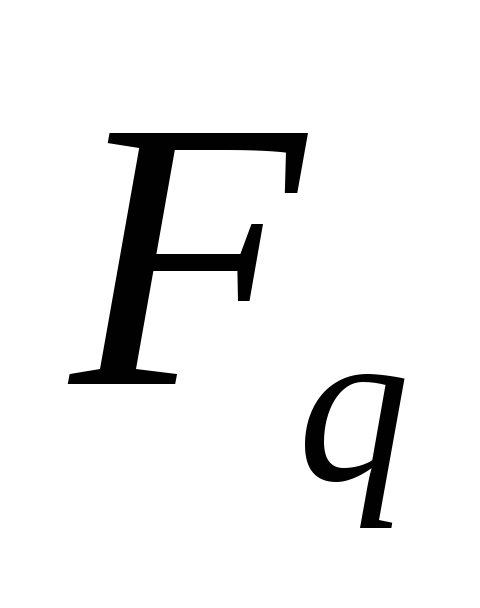 ?
?
