
- •1. Основні означення та необхідні відомості з теорії груп та кілець
- •2. Кільця лишків за модулем m
- •3. Кільця поліномів
- •3.1. Поліноми над кільцями
- •3.2. Поліноми над полями
- •3.3. Фактор-кільце f[X]/(f)
- •4. Корені поліномів та їх властивості
- •5. Поля часток
- •Підполя. Прості поля. Характеристики полів
- •Розширення полів
- •Алгебраїчні розширення
- •9. Мінімальні поліноми
- •Прості розширення полів та їх побудова
- •Поля розкладу поліномів
- •12. Теорема про існування та єдиність скінченних полів
- •13. Критерій підполя, діаграми включення підполів
- •14. Мультиплікативна група скінченного поля
- •Наслідки теореми 30.
- •15. Незвідні поліноми та їх корені
- •16. Спряжені елементи
- •17. Зображення елементів скінченних полів
- •18. Порядки поліномів
- •19. Примітивні поліноми
- •20. Сліди та норми
- •21. Базиси
- •22. Автоморфізми скінченних полів
- •23. Зведення основних положень та результатів
- •Предметний покажчик
- •Список використаної літератури
16. Спряжені елементи
Нехай
![]() .
Елементи
.
Елементи
![]() називаються спряженими
з
називаються спряженими
з
![]() відносно поля
відносно поля
![]() .
.
Спряжені
з
![]() відносно
відносно
![]() елементи будуть різними тоді і тільки
тоді, коли степінь мінімального полінома
елемента
елементи будуть різними тоді і тільки
тоді, коли степінь мінімального полінома
елемента
![]() дорівнює
дорівнює
![]() .
Якщо ж степінь мінімального полінома
.
Якщо ж степінь мінімального полінома
![]() дорівнює
d
(
дорівнює
d
(![]() ),
то різних спряжених елементів буде
рівно d:
),
то різних спряжених елементів буде
рівно d:
![]() ,
а далі вони повторюватимуться:
,
а далі вони повторюватимуться:![]() ,
…, і таких повторень буде m/d.
,
…, і таких повторень буде m/d.
ТЕОРЕМА
34.
Елементи, спряжені з
![]() відносно довільного підполя, мають
однаковий порядок у мультиплікативній
групі
відносно довільного підполя, мають
однаковий порядок у мультиплікативній
групі
![]() .
.
Достатньо
довести,
що
однаковий
порядок мають
элемент
та
q.
Відомо,
що
в циклічній
групі
<a>![]() (з
твірним
(з
твірним
![]() )
порядку
)
порядку
![]() порядок элемента аd
дорівнює
порядок элемента аd
дорівнює
![]() .
(Дійсно,
нехай
.
(Дійсно,
нехай
![]() ,
,
![]() ,
d=d1s,
причому
,
d=d1s,
причому
![]() Розглянемо
послідовність
Розглянемо
послідовність
![]() ;
вперше
;
вперше
![]() при kd
кратному
m,
але
в силу взаємної
простоти
при kd
кратному
m,
але
в силу взаємної
простоти
![]() і
і
![]() це вперше
станеться
при
це вперше
станеться
при
![]() :
:
![]() .
Таким
чином,
элемент d
породжує
циклічну
підгрупу
порядку
.
Таким
чином,
элемент d
породжує
циклічну
підгрупу
порядку
![]() =
=![]() .)
Нехай
порядок элемента
в
.)
Нехай
порядок элемента
в
![]() дорівнює
дорівнює
![]() .
Тоді
порядок циклічної
підгрупи
<α>
також
дорівнює
m
і
за
теор.
Лагранжа
.
Тоді
порядок циклічної
підгрупи
<α>
також
дорівнює
m
і
за
теор.
Лагранжа
![]() .
Элемент q
породжує
в <α>
підгрупу
порядку
.
Элемент q
породжує
в <α>
підгрупу
порядку
![]() .
Але
так як
(
.
Але
так як
(![]() ,
то і
(m,q)
= 1; отже,
порядок
,
то і
(m,q)
= 1; отже,
порядок
![]() ,
а таким
чином і
порядок q
,
дорівнює
m
, що
і
треба
було
довести.
,
а таким
чином і
порядок q
,
дорівнює
m
, що
і
треба
було
довести.
Наслідки теореми 34.
-
Елементи, спряжені з примітивним, також є примітивними.
-
Нехай
 ,
,
 – незвідний поліном. Тоді всі його
корені мають однаковий порядок у
мультиплікативній групі
– незвідний поліном. Тоді всі його
корені мають однаковий порядок у
мультиплікативній групі
 .
.
Приклад.
Нехай
![]() - корінь полінома
- корінь полінома
![]() над
над
![]() .
Елементи, спряжені з
.
Елементи, спряжені з
![]() відносно
відносно
![]() ,
–
це
,
–
це
![]() ,
а відносно
,
а відносно
![]() –
це
–
це
![]() та
та
![]() ;
всі вони є примітивними.
;
всі вони є примітивними.
17. Зображення елементів скінченних полів
Якщо
скінченне поле
![]() розглядати як фактор-кільце
розглядати як фактор-кільце
![]() ,
де
,
де
![]() -незвідний поліном степеня
-незвідний поліном степеня
![]() над
над
![]() ,
то елементи
,
то елементи
![]() можна збразити у вигляді поліномів над
можна збразити у вигляді поліномів над
![]() степеня
меншого за n:
степеня
меншого за n:
![]() ,
,
![]() ,
,
або у вигляді векторів:
![]() ,
,
![]() .
.
Еквівалентний
спосіб зображення елементів скіченного
поля випливає з теор.23:
якщо
![]() - корінь незвідного над
- корінь незвідного над
![]() полінома
полінома
![]() степеня
степеня
![]() ,
то
,
то
![]()
![]() утворюють базис у полі
утворюють базис у полі
![]() і будь-який елемент
і будь-який елемент
![]() зображується як лінійна комбінація
зображується як лінійна комбінація
![]()
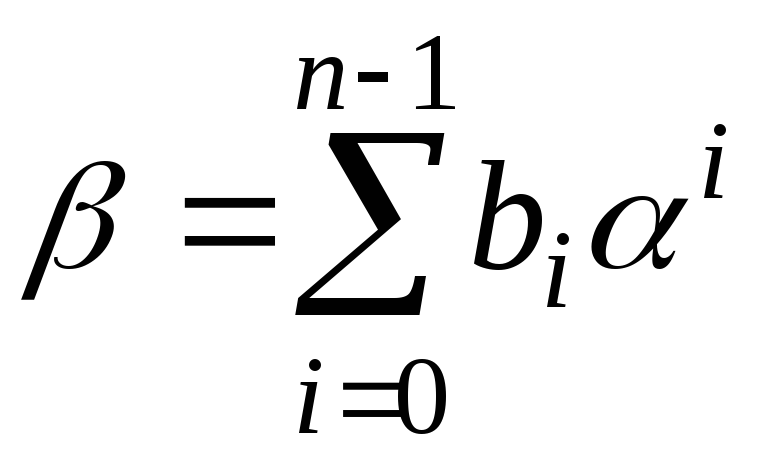 .
.
Ці три зображення елементів скіченного поля по суті є одним й тим самим.
Інше
зображення елементів скіченного поля
– це зображеня у вигляді степенів
деякого примітивного елемента
![]() .
.
Приклад.
Розглянемо
поле
![]() =
=
![]()
![]() ,
де
,
де
![]() – незвідний над
– незвідний над
![]() .
Нехай
.
Нехай
![]() –
корінь
полінома
–
корінь
полінома
![]() .
Тоді 1,
.
Тоді 1,![]() - базис
- базис
![]() над
над
![]() :
:
![]() ,
,
![]() .
Спробуємо зобразити всі елементи поля
.
Спробуємо зобразити всі елементи поля
![]() у вигляді степенів примітивного елемента.
Спочатку знайдемо примітивний елемент.
Розглянемо елемент
у вигляді степенів примітивного елемента.
Спочатку знайдемо примітивний елемент.
Розглянемо елемент
![]() :
так як
:
так як
![]() –
корінь
–
корінь
![]() ,
то
,
то
![]() ,
звідки
,
звідки
![]() ,
тобто
,
тобто
![]() –
не примітивний елемент (відповідно,
–
не примітивний елемент (відповідно,
![]() - не примітивний поліном).
- не примітивний поліном).
Розглянемо
тепер елемент
![]() .
Будемо підносити його у степені і
результату співставляти вектор
коефіцієнтів з
.
Будемо підносити його у степені і
результату співставляти вектор
коефіцієнтів з
![]() :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1, 0, 0, 0) |
|
|
(0, 1, 1, 1) |
|
|
(1, 0, 0, 1) |
|
|
(0, 1, 0, 0) |
|
|
(1, 1, 0, 0) |
|
|
(1, 0, 1, 1) |
|
|
(0, 0, 1, 0) |
|
|
(0, 1, 1, 0) |
|
|
(1, 0, 1, 0) |
|
|
|
Тобто
![]() – примітивний елемент. Звичайно, для
того, щоб перевірити примітивність
елемента
– примітивний елемент. Звичайно, для
того, щоб перевірити примітивність
елемента
![]() не потрібно було підносити його до всіх
степенів. Оскільки всі степені будь-якого
ненульового елемента утворюють підгрупу
мультиплікативної групи поля, то за
теоремою Лагранжа порядок елемента
повинен бути дільником порядку всієї
групи, тобто дільником 15. Таким чином,
для того, щоб перевірити, чи є елемент
не потрібно було підносити його до всіх
степенів. Оскільки всі степені будь-якого
ненульового елемента утворюють підгрупу
мультиплікативної групи поля, то за
теоремою Лагранжа порядок елемента
повинен бути дільником порядку всієї
групи, тобто дільником 15. Таким чином,
для того, щоб перевірити, чи є елемент
![]() примітивним
елементом поля, достатньо перевірити
рівності
примітивним
елементом поля, достатньо перевірити
рівності
![]() та
та
![]() .
Якщо жодна
з цих рівностей не виконується, то
.
Якщо жодна
з цих рівностей не виконується, то
![]() - примітивний.
- примітивний.
Проте
складена нами таблиця степенів
![]() дозволяє в явному вигляді представити
елементи поля
дозволяє в явному вигляді представити
елементи поля
![]() через степені примітивного елемента
через степені примітивного елемента
![]() .
.
Запис елементів скінченного поля у вигляді степенів примітивного елемента називається таблицею індексів. (Індекси – це показники відповідних степенів примітивного елемента).
Її зручно переписати в іншому вигляді:
|
Елемент |
Індекс |
Елемент |
Індекс |
|
|
15 |
(1, 0, 0, 1) |
8 |
|
(0, 0, 1, 0) |
12 |
(1, 0, 1, 0) |
14 |
|
|
1 |
(1, 0, 1, 1) |
11 |
|
(0, 1, 0, 0) |
9 |
(1, 1, 0, 0) |
10 |
|
|
2 |
|
5 |
|
(0, 1, 1, 0) |
13 |
|
4 |
|
(0, 1, 1, 1) |
7 |
|
3 |
|
(1, 0, 0, 0) |
6 |
|
|
За
допомогою таблиці індексів зручно
перемножати елементи скінченного поля.
Наприклад,
![]() або
або
![]()
У
загальному випадку множення у
![]() виконується за формулою:
виконується за формулою:![]() ,
де
,
де
![]() – примітивний елемент
– примітивний елемент
![]() .
.
