
- •1. Основні означення та необхідні відомості з теорії груп та кілець
- •2. Кільця лишків за модулем m
- •3. Кільця поліномів
- •3.1. Поліноми над кільцями
- •3.2. Поліноми над полями
- •3.3. Фактор-кільце f[X]/(f)
- •4. Корені поліномів та їх властивості
- •5. Поля часток
- •Підполя. Прості поля. Характеристики полів
- •Розширення полів
- •Алгебраїчні розширення
- •9. Мінімальні поліноми
- •Прості розширення полів та їх побудова
- •Поля розкладу поліномів
- •12. Теорема про існування та єдиність скінченних полів
- •13. Критерій підполя, діаграми включення підполів
- •14. Мультиплікативна група скінченного поля
- •Наслідки теореми 30.
- •15. Незвідні поліноми та їх корені
- •16. Спряжені елементи
- •17. Зображення елементів скінченних полів
- •18. Порядки поліномів
- •19. Примітивні поліноми
- •20. Сліди та норми
- •21. Базиси
- •22. Автоморфізми скінченних полів
- •23. Зведення основних положень та результатів
- •Предметний покажчик
- •Список використаної літератури
3. Кільця поліномів
3.1. Поліноми над кільцями
Нехай
![]() –
кільце,
–
кільце,
![]() – деякий символ, змінна.
– деякий символ, змінна.
Поліномом
над кільцем
![]() називається
вираз виду
називається
вираз виду
![]() ,
,
де
елементи
![]()
![]() ,
,
![]() називаються коефіцієнтами
полінома,
a0
називається
вільним
членом
полінома.
називаються коефіцієнтами
полінома,
a0
називається
вільним
членом
полінома.
Якщо
замість символа
![]() у вираз для
у вираз для
![]() підставити елемент
підставити елемент
![]() ,
то в
,
то в
![]() можна обчислити елемент
можна обчислити елемент
![]() ,
який
називається значенням
полінома в
точці
,
який
називається значенням
полінома в
точці
![]() .
.
Якщо
![]() ,
то поліном називається нульовим.
,
то поліном називається нульовим.
Якщо
поліном
![]() не
нульовий,
то існує
не
нульовий,
то існує
![]() таке, що
таке, що

Число
![]() ,
що задовольняє цій умові, називається
степенем
полінома
,
що задовольняє цій умові, називається
степенем
полінома
![]() і
позначається
і
позначається
![]() ,
,
![]() називається старшим
коефіцієнтом
полінома
називається старшим
коефіцієнтом
полінома
![]() .
Степінь нульового полінома за означенням
дорівнює
.
Степінь нульового полінома за означенням
дорівнює
![]() .
.
Говорять,
що поліном
![]() рівний
поліному
рівний
поліному
![]() і позначають цей факт як
і позначають цей факт як
![]() тоді і тільки тоді, коли їх відповідні
коефіцієнти рівні.
тоді і тільки тоді, коли їх відповідні
коефіцієнти рівні.
Введемо
операції додавання і множення на множині
поліномів над кільцем
![]() .
Нехай
.
Нехай
![]() ,
,
![]() ,
,
![]() і нехай для визначеності
і нехай для визначеності
![]()
Тоді вважаємо
![]() (вважається,
що при
(вважається,
що при
![]()
![]() ),
(2)
),
(2)
![]() ,
де
,
де
 .
(3)
.
(3)
ТЕОРЕМА
3.
Множина поліномів над кільцем
![]() з
введеними операціями додавання і
множення утворює кільце з нульовим
поліномом як нейтральним елементом за
додаванням (нулем).
з
введеними операціями додавання і
множення утворює кільце з нульовим
поліномом як нейтральним елементом за
додаванням (нулем).
Це кільце
позначають
![]() .
.
Справедливість теор.3 випливає з того, що коефіцієнти поліномів належать кільцю.
ТЕОРЕМА
4. (Про степені поліномів).
Нехай
![]() .
Тоді:
.
Тоді:
![]() ,
,
![]() .
.
Якщо
![]() –
область цілісності, то
–
область цілісності, то
![]() .
.
Якщо
![]() ,
то, очевидно,
,
то, очевидно,
![]() . Таким чином,
. Таким чином,
![]() є підкільцем
є підкільцем
![]() .
.
Кільце
![]() успадковує багато властивостей кільця
успадковує багато властивостей кільця
![]() .
.
ТЕОРЕМА 5.
-
Якщо
 –
кільце
з одиницею, то
–
кільце
з одиницею, то
 – кільце з одиницею.
– кільце з одиницею. -
Якщо
 –
комутативне кільце, то
–
комутативне кільце, то
 – теж комутативне.
– теж комутативне. -
Якщо
 – область цілісності, то
– область цілісності, то
 –
теж
цілісне.
–
теж
цілісне.
3.2. Поліноми над полями
Нехай
![]() –
поле,
–
поле,
![]() – множина поліномів над
– множина поліномів над
![]() .
.
Поліном
![]()
![]()
![]() ділиться
на поліном
ділиться
на поліном
![]()
![]()
![]() ,
якщо існує поліном
,
якщо існує поліном
![]()
![]() такий, що
такий, що
![]() =
=
![]()
![]() (цей факт будемо позначати як
(цей факт будемо позначати як
![]() –
“
–
“![]() ділить
ділить
![]() “).
“).
Так
само, як і у кільці
![]() ,
у
,
у
![]() можливе ділення з лишком.
можливе ділення з лишком.
ТЕОРЕМА
6.
Множина поліномів
![]() над полем
над полем
![]() з
операціями додавання та множення,
визначеними рівностями (1), (2),
утворює
евклідове кільце, тобто
з
операціями додавання та множення,
визначеними рівностями (1), (2),
утворює
евклідове кільце, тобто
![]() –
область цілісності і якщо
–
область цілісності і якщо
![]() ,
,
![]() то існують поліноми
то існують поліноми
![]() такі, що
такі, що![]() ,
де
,
де
![]() .
.
Приклад.
Розглянемо
приклад ділення з лишком поліномів з
![]() .
.

Тобто
![]() .
Тут
.
Тут
![]() ,
,
![]() (Нагадаємо, що операції над коефіцієнтами
виконуються за mod
5).
(Нагадаємо, що операції над коефіцієнтами
виконуються за mod
5).
Поліном називається нормованим (зведеним, унітарним), якщо його старший коефіцієнт дорівнює одиниці.
Нормований
поліном
![]() називається найбільшим
спільним дільником поліномів
називається найбільшим
спільним дільником поліномів
![]() і
і
![]() ,
якщо
,
якщо
![]() ,
,
![]() і
і
![]() .
.
ТЕОРЕМА
7.
Нехай
![]() .
Тоді існує єдиний нормований поліном,
що є найбільшим спільним дільником
поліномів
.
Тоді існує єдиний нормований поліном,
що є найбільшим спільним дільником
поліномів![]() ,
причому він може бути представлений у
вигляді їх лінійної комбінації:
,
причому він може бути представлений у
вигляді їх лінійної комбінації:
![]() ,
,
![]() .
.
Нормований
поліном
![]() називається найменшим
спільним кратним поліномів
називається найменшим
спільним кратним поліномів
![]() і
і
![]() ,
якщо
,
якщо
![]() ,
,
![]() і
і
![]() .
.
ТЕОРЕМА
8.
Кільце
поліномів
![]() є кільцем головних ідеалів, причому
кожен ідеал цього кільця породжується
нормованим поліномом.
є кільцем головних ідеалів, причому
кожен ідеал цього кільця породжується
нормованим поліномом.
![]() – область
цілісності (за теор.5).
Розглянемо
довільний ненульовий ідеал
– область
цілісності (за теор.5).
Розглянемо
довільний ненульовий ідеал
![]() .
Він містить деякий поліном
.
Він містить деякий поліном
![]() мінімального степеня. Нехай
мінімального степеня. Нехай
![]() –
коефіцієнт при старшому степені
–
коефіцієнт при старшому степені
![]() ,
тоді покладемо
,
тоді покладемо
![]() .
Покажемо, що
.
Покажемо, що
![]() ,
тобто,
,
тобто,
![]() ,
,![]() .
.
Оскільки
![]() – евклідове кільце, то
– евклідове кільце, то
![]() ,
,
![]() ,
,
![]() .
Якщо
.
Якщо![]() ,
то і
,
то і
![]() оскільки
оскільки
![]() і
і
![]() - підкільце. З причини
- підкільце. З причини
![]() ,
де
,
де
![]() –
ненульовий поліном мінімального степеня,
що належить
–
ненульовий поліном мінімального степеня,
що належить![]() ,
маємо
,
маємо
![]() ,
тобто,
,
тобто,
![]() ,
,
![]() ,
отже,
,
отже,
![]() .
.
Якщо в
ідеалі є ненульові константи, то,
очевидно,
![]() рівний
одиниці і
рівний
одиниці і
![]() .
.
Поліном
![]() називається незвідним,
якщо
називається незвідним,
якщо
![]()
![]() або
або![]() ,
,
![]() .
.
Незвідний
поліном не розкладається в добуток
двох поліномів додатних степенів.
Інакше: незвідний поліном ділиться
тільки на себе і на константи (елементи
поля
![]() ).
).
Звідність або незвідність полінома залежить від того, над яким полем він розглядається.
Приклади.
-
Поліном
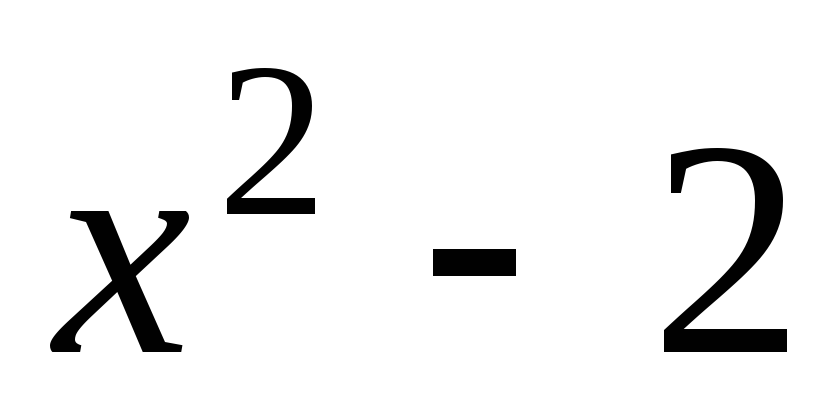 незвідний над полем раціональних чисел
Q,
але розкладається над полем дійсних
чисел R
:
незвідний над полем раціональних чисел
Q,
але розкладається над полем дійсних
чисел R
:
![]() .
.
-
Поліном
 незвідний над
незвідний над
 ,
але розкладається над
,
але розкладається над
 :
:
![]() .
.
ТЕОРЕМА
9 (про канонічний розклад).
Будь-який поліном
![]() представляється у вигляді
представляється у вигляді
![]() ,
,
де
![]() ,
,
![]() ,
,
![]() –
нормовані
незвідні поліноми,
–
нормовані
незвідні поліноми,
![]() - натуральні числа.
- натуральні числа.
