
- •1. Основні означення та необхідні відомості з теорії груп та кілець
- •2. Кільця лишків за модулем m
- •3. Кільця поліномів
- •3.1. Поліноми над кільцями
- •3.2. Поліноми над полями
- •3.3. Фактор-кільце f[X]/(f)
- •4. Корені поліномів та їх властивості
- •5. Поля часток
- •Підполя. Прості поля. Характеристики полів
- •Розширення полів
- •Алгебраїчні розширення
- •9. Мінімальні поліноми
- •Прості розширення полів та їх побудова
- •Поля розкладу поліномів
- •12. Теорема про існування та єдиність скінченних полів
- •13. Критерій підполя, діаграми включення підполів
- •14. Мультиплікативна група скінченного поля
- •Наслідки теореми 30.
- •15. Незвідні поліноми та їх корені
- •16. Спряжені елементи
- •17. Зображення елементів скінченних полів
- •18. Порядки поліномів
- •19. Примітивні поліноми
- •20. Сліди та норми
- •21. Базиси
- •22. Автоморфізми скінченних полів
- •23. Зведення основних положень та результатів
- •Предметний покажчик
- •Список використаної літератури
19. Примітивні поліноми
Поліном
![]() ,
,
![]() називається примітивним,
якщо він є мінімальним поліномом деякого
примітивного елемента
називається примітивним,
якщо він є мінімальним поліномом деякого
примітивного елемента
![]() над Fq.
над Fq.
ТЕОРЕМА
41.
Поліном![]() ,
,![]() ,
є примітивним над
,
є примітивним над
![]() тоді і тільки тоді, коли f
–
нормований,
тоді і тільки тоді, коли f
–
нормований,
![]() і
і
![]() .
.
Позначимо
![]() .
.
Якщо f
примітивний,
то він є мінімальним поліномом деякого
примітивного елемента. Отже, f
нормований, незвідний,
![]() ,
а
його корені мають порядок
,
а
його корені мають порядок
![]() .
Таким
чином, за
теор. 36
і
.
Таким
чином, за
теор. 36
і
![]() .
.
Навпаки:
![]() .
Доведемо, що
.
Доведемо, що
![]() – незвідний. Від супротивного: нехай
– незвідний. Від супротивного: нехай
![]() – звідний. Тоді або 1)
– звідний. Тоді або 1)
![]() ,
де
,
де
![]() – незвідний,
– незвідний,
![]() натуральне, або 2)
натуральне, або 2)
![]() ,
де
,
де
![]()
![]() У випадку 1)
У випадку 1)
![]() має ділитися на
має ділитися на
![]() (теор.38),
але
(теор.38),
але
![]() ,
а
,
а
![]() –
протиріччя. У випадку 2) за
теор.
39
–
протиріччя. У випадку 2) за
теор.
39
![]() –
знову ж таки протиріччя з умовою.
Таким чином,
–
знову ж таки протиріччя з умовою.
Таким чином,
![]() – незвідний і за насл.
з теор.34
всі його корені – примітивні. Отже,
– незвідний і за насл.
з теор.34
всі його корені – примітивні. Отже,
![]() – примітивний.
– примітивний.
Зауважимо,
що умова
![]() потрібна лише, щоб виключити випадок
потрібна лише, щоб виключити випадок
![]() .
.
Теорема 41 дає ще одне визначення примітивного полінома:
Нормований
незвідний поліном
![]() над
над
![]()
![]() ,
,
![]() ,
називається примітивним,
якщо
,
називається примітивним,
якщо
![]() .
.
ТЕОРЕМА
42.
Кількість
примітивних
поліномів степеня
![]() над
над
![]()
![]() дорівнює
дорівнює
![]() ,
де
,
де
![]() - функція Ейлера.
- функція Ейлера.
Примітивні
поліноми незвідні. Тому всі корені
примітивних поліномів степеня
![]() лежать у
лежать у
![]() (теор.33).
За
наслідком
1 теор.30 кількість
примітивних елементів поля
(теор.33).
За
наслідком
1 теор.30 кількість
примітивних елементів поля
![]() дорівнює
дорівнює
![]() .
Оскільки кожен примітивний поліном
степеня
.
Оскільки кожен примітивний поліном
степеня
![]() має рівно
має рівно
![]() коренів і всі вони різні (теор.33)
і
примітивні (наслідки
1,2 теор.34),
то кількість примітивних поліномів
дорівнює
коренів і всі вони різні (теор.33)
і
примітивні (наслідки
1,2 теор.34),
то кількість примітивних поліномів
дорівнює
![]() .
.
Контролні питання до §16-19
-
Дати визначення спряжених елементів.
-
Назвіть способи зображення елементів скінченого поля.
-
Дати визначення порядку полінома. Сформулювати теореми, що дозволяють визначити порядок поліномів над скінченним полем.
-
Дати визначення примітивного поліному, незвідного поліному.
Скільки існує примітивних поліномів степеня п над заданим скінченим полем?
Задачі до §16-19
-
Знайти кількість незвідних поліномів степеню від 1 до 6 над
 .
. -
Знайти всі незвідні поліноми степеню 2 та 3 над
 .
. -
Знайти всі примітивні поліноми степеню 3 над
 і степеню 2 над
і степеню 2 над
 .
. -
Які з наступних поліномів є незвідними? Примітивними?
-
 ;
;
-
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
-
Довести: якщо l – просте, то кількість незвідних поліномів степені l над
 дорівнює
дорівнює

-
Довести: кількість примітивних поліномів степені п над
 дорівнює
дорівнює
 ,
де φ
– функція Ойлера.
,
де φ
– функція Ойлера. -
Подати всі елементи поля
 у вигляді степенів деякого примітивного
елемента.
у вигляді степенів деякого примітивного
елемента. -
До трьох з елементів поля знайти обернені відносно множення та обернені відносно додавання.
-
Знайти порядок поліному
 над
над
 .
. -
Нехай
 - прості корені поліному f.
Довести:
- прості корені поліному f.
Довести: .
. -
Нехай
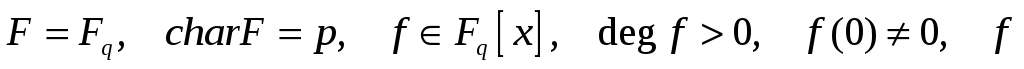 -
незвідний. Довести:
-
незвідний. Довести:
 .
. -
Довести:
 .
. -
Знайти порядки всіх нормованих незвідних поліномів степені 3 над
 .
. -
Нехай поліном f - з задачі 10. Знайти загальну формулу, що пов’язує порядки поліномів f та f в.
20. Сліди та норми
Нехай
![]() ,
,
![]() (
(![]() ).
).
Слідом
елемента
![]() над полем
над полем
![]() називається
сума всіх елементів, спряжених з
називається
сума всіх елементів, спряжених з
![]() відносно
поля
відносно
поля
![]() :
:
![]() .
.
Якщо
![]() –
просте підполе (
–
просте підполе (![]() ),
то слід називається абсолютним
і позначається:
),
то слід називається абсолютним
і позначається:
![]() .
.
Нехай
![]() – мінімальний поліном елемента
– мінімальний поліном елемента
![]() (він завжди незвідний). Якщо deg
f
= n,
то
його коренями є α,
αq,
…,
(він завжди незвідний). Якщо deg
f
= n,
то
його коренями є α,
αq,
…,![]() (теор.33).
Якщо
deg
f
=
(теор.33).
Якщо
deg
f
=![]() ,
то d
повинно
ділити n
(див. теор.
23, п. 3)).
Розглянемо поліном
,
то d
повинно
ділити n
(див. теор.
23, п. 3)).
Розглянемо поліном
![]() ,
,
![]() .
Він буде нормованим і мати вид
.
Він буде нормованим і мати вид
![]() .
.
Його
коренями є
![]() ,
кожен кратності
,
кожен кратності
![]() .
Враховуючи кратність, їх теж можна
позначити як
.
Враховуючи кратність, їх теж можна
позначити як
![]() .
Всі корені
.
Всі корені
![]() лежать
в
лежать
в![]() ,
тому в
полі
,
тому в
полі
![]() він розкладається в добуток:
він розкладається в добуток:
![]()
Звідки,
прирівнюючи коефіцієнти, одержуємо
![]() ,
що дорівнює сліду елемента
,
що дорівнює сліду елемента
![]() над полем
над полем
![]() .
Так як
.
Так як
![]() ,
можна зробити висновок, що слід елемента
,
можна зробити висновок, що слід елемента
![]() лежить в
лежить в
![]() ,
тобто маємо відображення
,
тобто маємо відображення
![]() (див. рисунок).
(див. рисунок).
 Поліном
Поліном
![]() називається
характеристичним
поліномом елемента
називається
характеристичним
поліномом елемента
![]() .
.
ТЕОРЕМА
43 (властивості сліду).
Нехай![]() ,
,
![]() .
Тоді мають місце такі властивості:
.
Тоді мають місце такі властивості:
-
Якщо
 ,
то
,
то
 .
.
 .
.
-
Якщо
 ,
,
 ,
то
,
то
 .
.
 .
.
-
 – сюр'єктивне
лінійне відображення F
на
– сюр'єктивне
лінійне відображення F
на
 як
лінійних векторних просторів.
як
лінійних векторних просторів.
Лінійність
доведена в пп.
1), 2).
Доведемо сюр'єктивність.
Для цього достатньо показати, що
![]() ,
оскільки якщо
,
оскільки якщо
![]() пробігає всі елементи
пробігає всі елементи
![]() ,
то за властивістю 2)
одержимо
,
то за властивістю 2)
одержимо
![]() – теж пробігає всі елементи
– теж пробігає всі елементи
![]() .
Будь-який елемент
.
Будь-який елемент
![]() такий, що
такий, що
![]() ,
є коренем полінома
,
є коренем полінома
![]() .
Але оскільки даний поліном має не більше,
ніж
.
Але оскільки даний поліном має не більше,
ніж
![]() коренів, а поле F
містить
коренів, а поле F
містить
![]() елементів,
то в ньому існують потрібні нам елементи:
елементів,
то в ньому існують потрібні нам елементи:
![]() .
.
-
 ,
де
,
де
 – степінь розширення F
над
– степінь розширення F
над
 .
.
![]() так як
так як
![]() .
.
-
 .
.

Слід не
тільки сам є лінійним відображенням –
через нього виражаються всі лінійні
відображення з
![]() у
у
![]() .
.
ТЕОРЕМА
44.
Будь-яке
лінійне відображення з
![]() у
у
![]() є відображенням
є відображенням
![]() ,
,
![]() виду
виду
![]() .
При цьому
.
При цьому
![]() ,
якщо
,
якщо
![]() .
.
Кожне
відображення
![]() за теор.
43 є
лінійним відображенням
за теор.
43 є
лінійним відображенням
![]() на
на
![]() .
При цьому, якщо
.
При цьому, якщо
![]() ,
то
,
то
![]()
для
відповідним чином вибраного елемента
![]() .
Тому
.
Тому
![]() та
та
![]() відмінні. Так як у
відмінні. Так як у
![]()
![]() елементів, то одержуємо
елементів, то одержуємо
![]() різних лінійних відображень із
різних лінійних відображень із
![]() у
у
![]() .
З іншого боку, взявши деякий базис
.
З іншого боку, взявши деякий базис
![]() векторного простору
векторного простору
![]() над
над
![]() ,
ми можемо отримати будь-яке лінійне
відображення
,
ми можемо отримати будь-яке лінійне
відображення
![]() у
у
![]() ,
відображаючи базисні елементи
,
відображаючи базисні елементи
![]() у довільні елементи поля
у довільні елементи поля
![]() Це можна зробити
Це можна зробити
![]() різними способами; отже, всі лінійні
відображення
різними способами; отже, всі лінійні
відображення
![]() у
у
![]() вичерпуються відображеннями
вичерпуються відображеннями
![]() ,
,
![]() .
.
ТЕОРЕМА
45 (про
транзитивність
сліду).
Нехай
![]() – башта розширень. Тоді
– башта розширень. Тоді
![]() (див. рисунок).
(див. рисунок).
 Нехай
Нехай
![]() ,
,
![]() .
Оскільки
.
Оскільки
![]() ,
,
![]() ,
,
![]() ,то
,то![]()

![]()
Нормою
елемента![]() над полем
над полем
![]() називається
добуток усіх елементів, спряжених з
називається
добуток усіх елементів, спряжених з
![]() відносно
поля
відносно
поля
![]() :
:
![]() .
.
Аналогічно
сліду можна показати, що![]()
![]() ,
де
,
де
![]() – вільний член характеристичного
полінома елемента
– вільний член характеристичного
полінома елемента
![]() .
.
ТЕОРЕМА 46 (властивості норми).
-
 .
. -
 – це
відображення F
на
– це
відображення F
на
 і
F*
на
K*.
і
F*
на
K*. -
 .
. -
 .
.
Читачу пропонується довести цю теорему в якості вправи.
