Решение практических задач по теме: «Плоскость»

П р и м е р 1. Определить отрезки, отсекаемые плоскостью 2 х – 3 у + 8 z – 4 = 0 на осях координат.

Решение. Приведем данное уравнение плоскости к уравнению в отрезках. Для этого свободный член перенесем в правую сторону, а затем каждое слагаемое разделим на него, т. е. на 4:

.

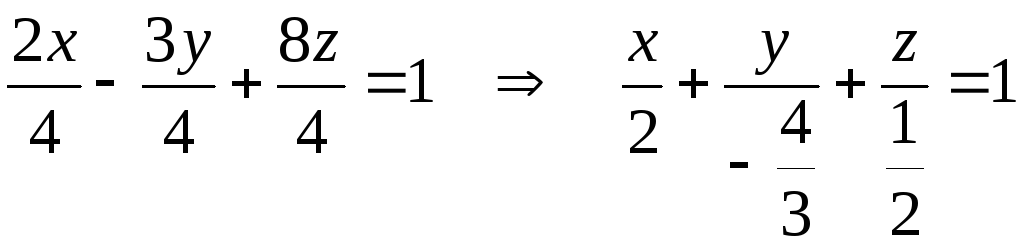Следовательно плоскость отсекает по оси Ох отрезок равный а = 2, по оси Оу – b = – 3/4, по оси Oz – с = 1/2.

П р и м е р 2. Найти уравнение плоскости, проходящей через точки А (2; – 1; 4) и В (3; 2; – 1) перпендикулярно к плоскости

х + у + z – 3 = 0.

Решение. В качестве нормального вектора искомой плоскости можно взять вектор, перпендикулярный вектору

и нормальному вектору данной плоскости. Поэтому за примем векторное произведение и :

.

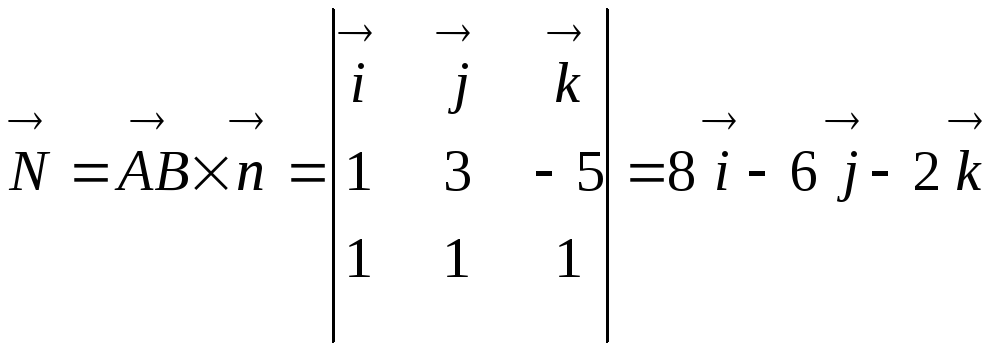Остается воспользоваться уравнением плоскости, проходящей через данную точку (например, точку А) перпендикулярно заданному вектору :

А (х – х₀) + В (у – у₀) + С (z – z₀) = 0

8 (х – 2) – 6 (у + 1) – 2 (z – 4) = 0 или 8 х – 6 у – 2 z – 14 = 0.

П р и м е р 3. Построить плоскости:

а) 3 х + 4 у – 6 z – 12 = 0;

б) y + z – 2 = 0;

в) y + z = 0;

г) 3 y – 7 = 0.

Решение. а) Приведем данное уравнение к уравнению в отрезках:

.

Следовательно данная плоскость отсекает по оси Ох отрезок а = 4, по оси Оу – b = 3, по оси Оz – с = – 2.

б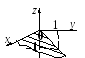) Так как в уравнении отсутствует координата х, то данная плоскость параллельна оси Ох и проходит через прямую .

в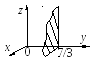) В уравнении отсутствует свободный коэффициент и переменная х, поэтому плоскость проходит через ось Ох, т. е. содержит ее. А также проходит через прямую y = – z.

г) В данном уравнении отсутствуют переменные х и z, поэтому плоскость проходит параллельно плоскости хОz и через прямую у = 7/3.

П р и м е р 4. Написать уравнение плоскости, проходящей через точки А (1; – 1; 2), В (2; 1; 2) и С (1; 1; 4).

Решение. Воспользуемся уравнением плоскости, проходящей через три точки:

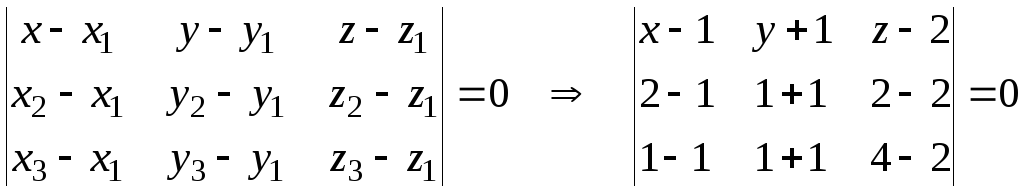
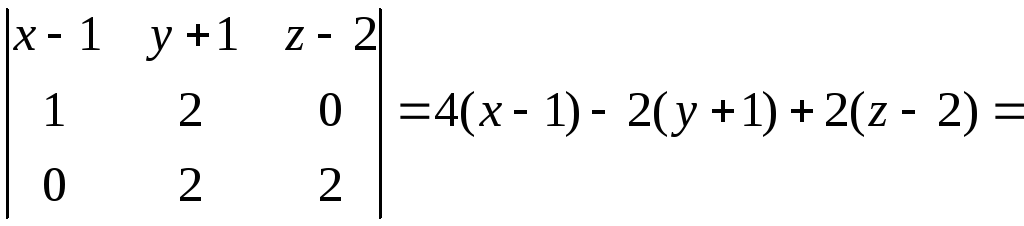
или

.

П р и м е р 5. Найти расстояние от точки (5; 1; – 1) до плоскости х – 2 у – 2 z + 4 = 0.

Решение. Используем формулу расстояния от точки до плоскости, находим

.

П р и м е р 6. Написать уравнение плоскости, проходящей через точку (2; – 1; 1) и перпендикулярной к плоскостям

3 х + 2 у – z + 4 = 0 и х + у + z – 3 = 0.

Решение. Очевидно, что в качестве нормального вектора искомой плоскости можно взять векторное произведение нормальных векторов и данных плоскостей:

.

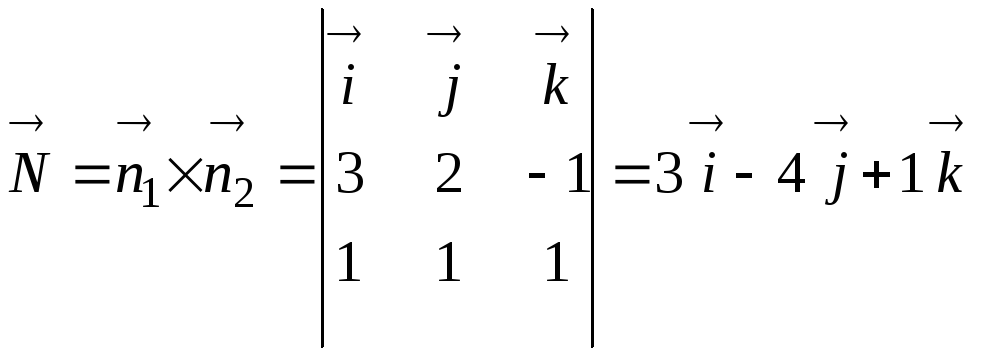Теперь, используя уравнение плоскости, проходящей через данную точку (2; – 1; 1) перпендикулярно вектору , получаем:

А (х – х₀) + В (у – у₀) + С (z – z₀) = 0

3 (х – 2) – 4 (у + 1) + 1 (z – 1) = 0 или 3 х – 4 у + z – 11 = 0.

П р и м е р 7. Найти угол между плоскостями 4 х + 3 у – 5 z – 8 = 0 и 4 х + 3 у – 5 z + 12 = 0.

Решение. Воспользуемся формулой:

,

где , – векторы нормалей к данным плоскостям, тогда

.

Следовательно, φ = arcos 1 = 0, т. е. плоскости параллельны.

Решение практических задач по теме: «Прямая в пространстве. Взаимное расположение прямой и плоскости»

П р и м е р 8. Привести к каноническому виду уравнения прямой:

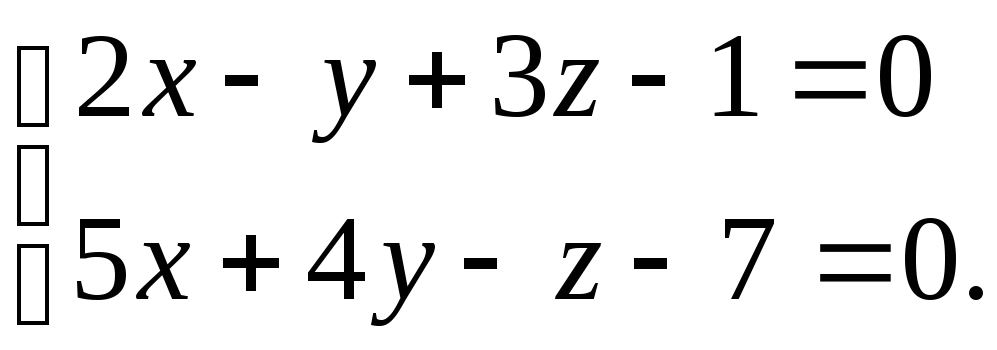
Решение. Найдем вектор перпендикулярный нормальным векторам , соответствующих плоскостей

.

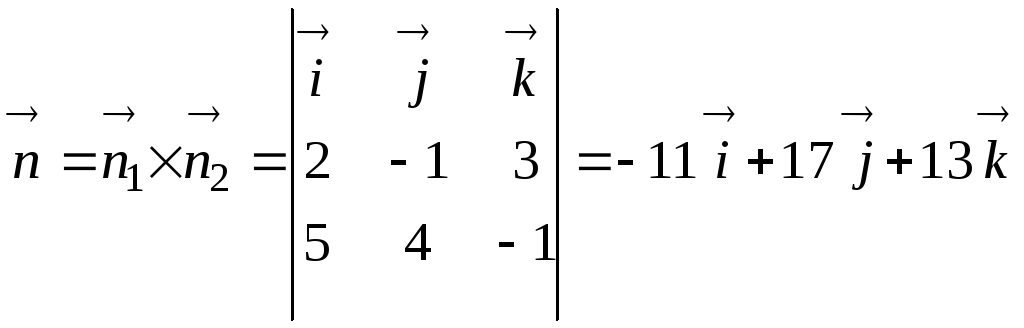В качестве точки М₁ (х₁, у₁, z₁), через которую проходит искомая прямая, можно взять точку пересечения ее с любой из координатных плоскостей, например с плоскостью уОz. Так как при этом х₁ = 0, то координаты у₁ и z₁ этой точки определятся из системы уравнений заданных плоскостей, если в них положить х = 0:

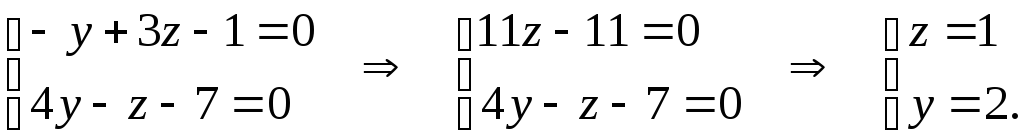
Итак, точка М₁ (0, 2, 1), а искомая прямая определяется уравнениями:

или

.

П р и м е р 9. Написать уравнение прямой, проходящей через точки А (– 1; 2; 3) и В (2; 6; – 2), и найти ее направляющие косинусы.

Решение. Воспользуемся формулой прямой, проходящей через две точки:

.

П р и м е р 10. Написать параметрические уравнения прямой, проходящей через точку (– 2; 1; – 1) и параллельной вектору .

Решение. Воспользуемся каноническими уравнениями прямой. Полагая в равенствах

l = 1, m = – 2, n = 3, x₁ = – 2, y₁ = 1, z₁ = – 1, получаем

.

Приравняем поочередно каждое уравнение к параметру t и получим

или

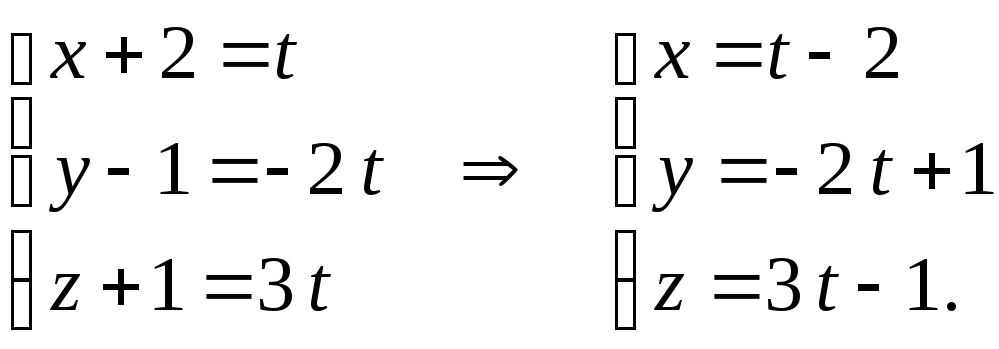
П р и м е р 11. Показать, что прямая лежит в плоскости 2 х + у – z = 0.

Решение. Должно быть одновременное выполнение равенств

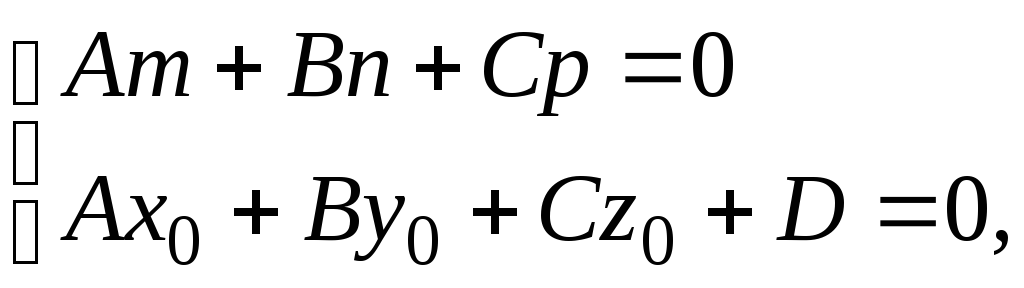
где А = 2, В = 1, С = – 1, D = 0, m = 2, n = – 1, p = 3, х₀ = – 1, у₀ = – 1, z₀ = – 3.

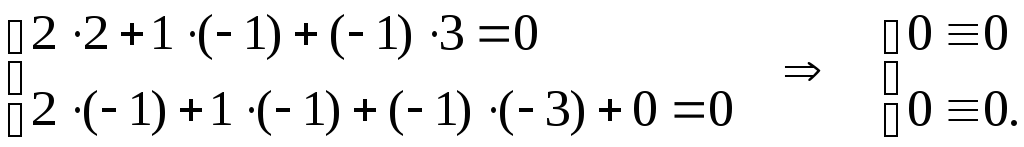
Следовательно, прямая принадлежит плоскости.

П р и м е р 12. Найти угол между прямой и плоскостью 2 х + у + z – 4 = 0.

Решение. Воспользуемся формулой:

где А = 2, В = 1, С = 1, m = – 2, n = – 6, p = 3.

Следовательно,