1. Угол между плоскостями.

Определение 3. Пусть даны две плоскости

П₁: А₁ х + В₁ у + С₁ z + D₁ = 0

П₂: А₂ х + В₂ у + С₂ z + D₂ = 0.

Углом между плоскостями П₁ и П₂ будем называть любой из двух смежных двугранных углов, образованных этими плоскостями (в случае параллельности плоскостей угол между ними можно считать равным 0 или π по желанию).

Угол между плоскостями или равен углу между их нормальными векторами, или равен смежному с ним углу, т. е.

или

или

Т е о р е м а 2. В декартовых координатах угол между плоскостями П₁ и П₂ определяется формулой

(2)

2. Условие перпендикулярности двух плоскостей

В случае перпендикулярности двух плоскостей угол между ними равен 90, следовательно, cos φ = 0. Из (2) следует, что

(3)

3. Условие параллельности двух плоскостей

Если плоскости П₁ и П₂ параллельны, то , т. е. . Переходя к координатам, это условие записывается следующим образом

(4)

4. Условие совпадения плоскостей

Пусть плоскости П₁ и П₂ заданы следующим образом:

П₁: А₁ х + В₁ у + С₁ z + D₁ = 0

П₂: А₂ х + В₂ у + С₂ z + D₂ = 0.

Для совпадающих плоскостей выполняется условие

.

Различные формы уравнений плоскости

1. Общее уравнение плоскости

А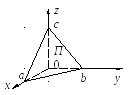 х + В у + С z + D = 0. (5)

2. Уравнение плоскости в отрезках. Пусть плоскость П пересекает оси декартовых координат в точках (а, 0, 0), (0, b, 0), (0, 0, с). Тогда – уравнение плоскости в отрезках.

Этим уравнением удобно пользоваться при построении плоскости.

3. Уравнение плоскости, проходящей через три данные точки М₁(x₁, y₁, z₁), М₂(x₂, y₂, z₂), М₃(x₃, y₃, z₃). Получается как условие ком-

п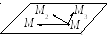ланарности трех векторов , , , где М (х, у, z) – текущая точка плоскости, т.е.

(6)

4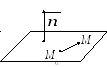. Уравнение плоскости, проходящей через данную точку М₀(х₀, у₀, z₀), и имеющую нормальный вектор . Получается как условие перпендикулярности двух векторов и , где М (х, у, z) – текущая точка плоскости, т.е.

А (х – х₀) + В (у – у₀) + С (z – z₀) = 0. (7)

5. Расстояние от точки до плоскости. Расстояние d от точки М₀(х₀, у₀, z₀) до плоскости П: А х + В у + С z + D = 0; находится по формуле

(8)

§ 2. Прямая в пространстве

Определение 4. Всякие две не параллельные между собой плоскости с общими уравнениями

П₁: А₁ х + В₁ у + С₁ z + D₁ = 0

П₂: А₂ х + В₂ у + С₂ z + D₂ = 0

определяют прямую их пересечения. Эти уравнения, рассматриваемые совместно, называются общими уравнениями прямой.

Определение 5. Ненулевой вектор , параллельный прямой или лежащий на ней, называется направляющим вектором этой прямой.

Взаимное расположение прямых в пространстве

У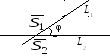глом между двумя прямыми L₁ и L₂ равен углу между их направляющими векторами и

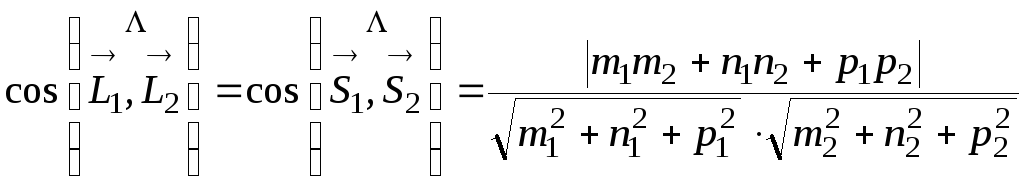. (9)

Условие перпендикулярности двух прямых

. (10)

Условие параллельности двух прямых

(11)

Различные виды уравнений прямой в пространстве

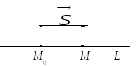1. Канонические уравнения прямой. Пусть М₀ (х₀, у₀, z₀) ∈ L; 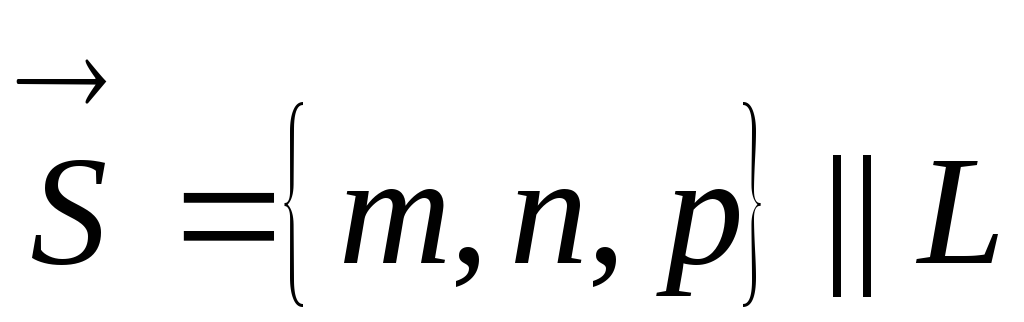; М (х, у, z) – произвольная точка прямой L. Векторы и коллинеарны, т. е.

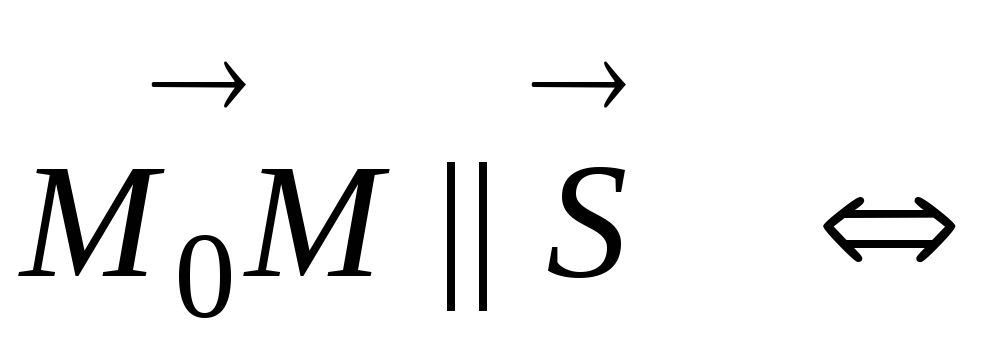
(12)

Полученные уравнения называются каноническими уравнениями прямой.

2. Параметрические уравнения прямой. Пусть прямая L задана каноническими уравнениями. Обозначим через t каждое из равных отношений. Тогда

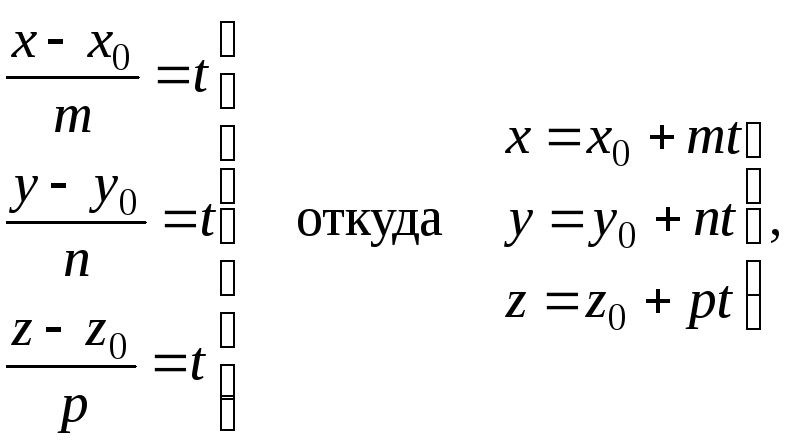
Полученные равенства называются параметрическими уравнениями прямой, а t – параметром прямой.

3. Уравнение прямой, проходящей через две точки. Пусть М₁(х₁, у₁, z₁) ∈ L, М₂(х₂, у₂, z₂) ∈ L, вектор

является направляющим для данной прямой.

Подставляя в канонические уравнения прямой координаты вектора и координаты точки М₁, получим уравнения прямой, проходящей через две заданные точки:

(13)

Приведение общих уравнений прямой к каноническому виду

От общих уравнений прямой можно перейти к ее каноническим уравнениям. Для этого нужно знать какую-либо точку М₀(х₀, у₀, z₀) прямой и ее направляющий вектор .

Пусть прямая задана общими уравнениями

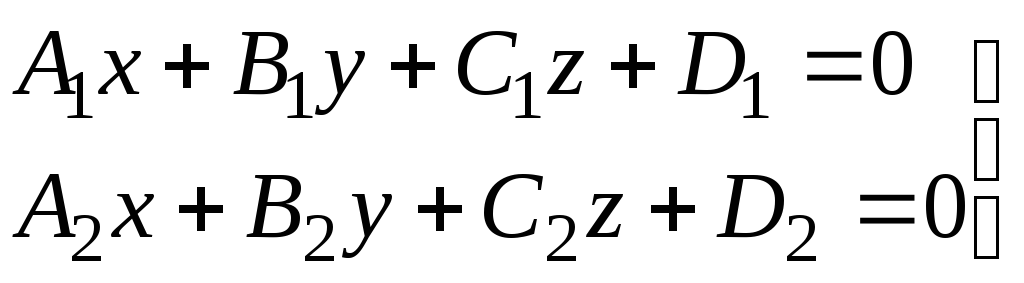(14)

Координаты точки М₀ на прямой получим из системы уравнений (6), придав одной из координат произвольное значение.

Так как прямая перпендикулярна нормальным векторам плоскостей найдем направляющий вектор прямой

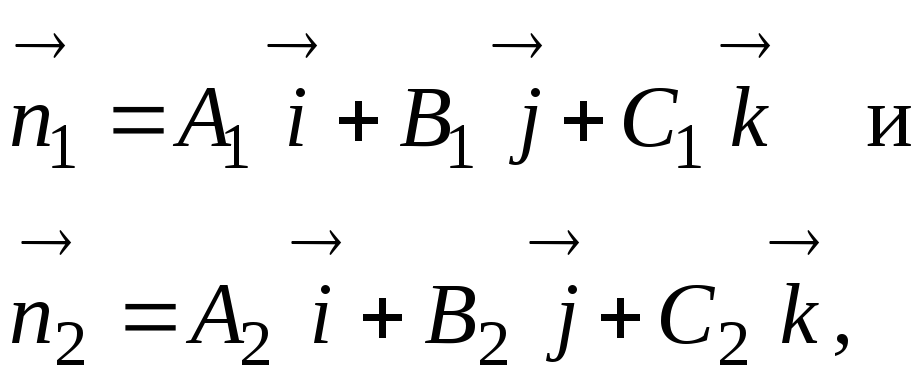
то за направляющий вектор прямой L можно принять векторное произведение :

.
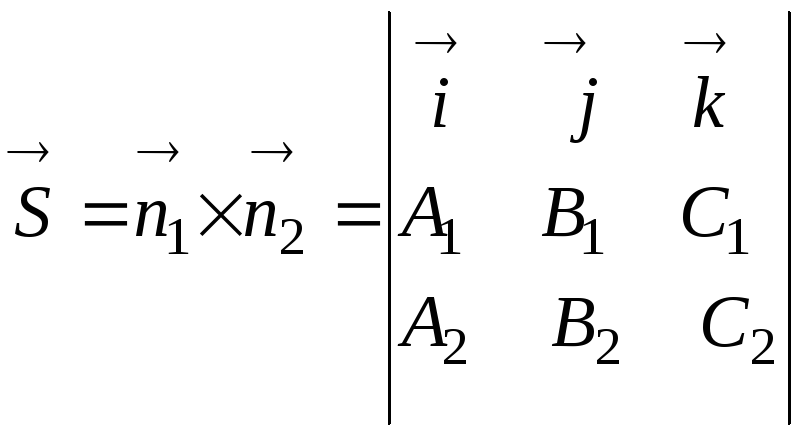