
- •Глава 7 Дифференциальное исчисление функции одной переменной
- •§ 1. Производная функции одной переменной
- •Правила дифференцирования
- •§ 2. Дифференциал функции одной переменной
- •§ 3. Производные и дифференциалы высших порядков
- •§ 4. Правило Лопиталя (1661 – 1704)
- •§ 5. Исследование функции одной переменной
- •Решение практических задач по теме «Производная функции одной переменной»
- •Решение практических задач по теме «Дифференциал функции одной переменной»
- •Решение практических задач по теме «Исследование функции одной переменной»
- •Примеры для самостоятельного решения.
Глава 7 Дифференциальное исчисление функции одной переменной
§ 1. Производная функции одной переменной
Определение 1. Производной функции у = f (x) называется величина, обозначаемая f ′(x) и равная пределу отношения приращения функции ∆у к приращению аргумента ∆х, когда ∆х стремиться к нулю, т. е.
![]()
Другие обозначения
у ;
![]()
Задачи, приводящие к понятию производной
1. Задача о касательной и нормали к кривой (геометрический смысл производной).
П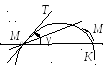 усть
М0
– фиксированная точка данной непрерывной
кривой К.
Рассмотрим секущую М0М,
проходящую через точку М0.
Пусть точка М
по кривой неограниченно приближается
к точке М0,
тогда секущая М0М
стремится к некоторому предельному
усть
М0
– фиксированная точка данной непрерывной
кривой К.
Рассмотрим секущую М0М,
проходящую через точку М0.
Пусть точка М
по кривой неограниченно приближается
к точке М0,
тогда секущая М0М
стремится к некоторому предельному
положению М0Т, т. е. угол γ стремится к нулю при М стремящемся к М0. Тогда предельная прямая МТ называется касательной, проведенной к кривой К в точке М0.
Определение 2. Касательной к данной непрерывной кривой в данной точке М0 (точка касания) называется предельное положение секущей М0М, проходящей через точку М0, когда точка М неограниченно приближается по кривой к точке М0.
П остановка
задачи.
Зная уравнение линии у
= f
(x),
найти уравнение касательной в данной
точке М (х,
у),
предполагая, что касательная существует.
остановка
задачи.
Зная уравнение линии у
= f
(x),
найти уравнение касательной в данной
точке М (х,
у),
предполагая, что касательная существует.
Пусть дана функция у = f (x). Пусть аргумент х0 получил некоторое
приращение ∆х. Тогда функция у получит приращение ∆у. Таким образом:
– при значении х0 будет иметь у = f (x0),
– при значении х0 + ∆х будет иметь у + ∆у = f (x0 + ∆x).
Выразим приращение функции ∆у = f (x0 + ∆x) – f (x0) и составим отношение
![]()
Найдем предел этого отношения при ∆х стремящемся к нулю. Если этот предел существует, то его называют согласно определению производной данной функции f (x) в точке х0 и обозначают f (x).
Возьмем на линии еще одну точку М (х0 + ∆х; у0 + ∆у). Проведем секущую ММ и прямые МN || Ох и МN || Оу. ∆ММ N – прямоугольный с катетами ∆х и ∆у. Из этого треугольника определяем угловой коэффициент секущей:
![]() (1)
(1)
Пусть теперь М → М, тогда ∆х → 0 и ММ → МТ – касательной в точке М. При ∆х → 0 угол φ → α и если МТ не перпендикулярна к оси Ох, то в силу непрерывности тангенса получим
tg φ → tg α.
Отсюда, переходя к пределу при ∆х → 0 в (1), найдем угловой коэффициент k = tg α касательной МТ:
![]() .
.
Таким образом, угловой коэффициент касательной, проведенной к графику функции y = f (x) равен значению ее производной в точке касания, т. е. k = f (x0). Зная угловой коэффициент касательной, легко написать ее уравнение:
Так как у – у0 = k (x – x0), y0 = f (x0), k = f (x0), то
y – y0 = f (x0) (x – x0).
Определение 3. Нормалью к кривой в точке М0 (х0, у0) называется перпендикуляр к касательной в той же точке.
Если k
– угловой коэффициент касательной, а
k1
– угловой коэффициент нормали, то
![]() ,
а т. к. k
= f
(x0)
легко записать уравнение нормали
,
а т. к. k
= f
(x0)
легко записать уравнение нормали
![]()
Если в точке х0 у0 = 0, то касательная параллельна оси Ох. Тогда нормаль перпендикулярна к оси Ох и проходит через точку М0 (х0, у0). Это означает, что ее уравнение: х = х0.
2. Задача о скорости прямолинейного неравномерного движения (механический смысл производной).
Пусть х – время, прошедшее от начала отсчета; у = f (x) – расстояние, которое прошло тело за время х от начала движения. Рассмотрим промежуток времени ∆х, прошедший от момента х до момента х + ∆х. За это время тело пройдет путь
∆у = f (x + ∆x) – f (x).
Отношение пройденного пути ∆у к промежутку времени ∆х называется средней скоростью движения тела за данный промежуток времени
![]() .
.
Средняя скорость тем лучше характеризует движение, чем меньше промежуток времени ∆х.
Тогда мгновенной скоростью движения тела в момент времени х будет предел средней скорости при неограниченном уменьшении промежутка времени ∆х (если этот предел существует):
![]() .
.
Полученное выражение представляет производную функции у по переменной х, т. е.
![]() .
.
Таким образом, скорость прямолинейного движения равна производной от пути по времени. Или, рассматривая функцию f (x) лишенную конкретного физического содержания, можно сказать, что производная функции y = f (x) в точке х есть скорость изменения функции в этой точке.
Рассмотрение задач о касательной и скорости движения исторически привело к понятию производной.
Итак,
![]() .
.
К подобному выражению приводят и многие другие задачи, что объясняет важность введения понятия производной. Процесс нахождения производной называется дифференцированием.
Определение 4. Если функция дифференцируема в каждой точке некоторого отрезка [a, b] или интервала (а, b), то говорят, что она дифференцируема на этом отрезке или интервале.
Т е о р е м а 1. (о связи между дифференцируемостью и непрерывностью функции)
Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна.
Доказательство. Пусть y = f (x) дифференцируема в точке х, т. е.
![]() .
.
Тогда определим
![]() .
.
По определению непрерывности следует, что y = f (x) – непрерывна. Что и требовалось доказать.
З амечание:
обратное утверждение неверно: непрерывная
функция может не иметь производной.
Например,
амечание:
обратное утверждение неверно: непрерывная
функция может не иметь производной.
Например,
![]() .
Эта функция непрерывна в точке х
= 0, но не
является дифференцируемой для этого
значения, т. к. в точке х
= 0 к графику функции не существует
касательной.
.
Эта функция непрерывна в точке х
= 0, но не
является дифференцируемой для этого
значения, т. к. в точке х
= 0 к графику функции не существует
касательной.
Правило непосредственного вычисления производной функции
Для нахождения производной функции у = f (x) необходимо произвести следующие действия:
-
Дать аргументу х приращение ∆х, вычислить наращенное значение функции f (x + ∆x);
-
Найти соответствующее приращение функции
∆y = f (x + ∆x) – f (x);
-
Составить отношение

-
Найти предел данного отношения при ∆х → 0
![]() ;
;
Будем пользоваться этим правилом для нахождения основных формул дифференцирования и вычисления производных от основных элементарных функций.
Основные правила дифференцирования
1. Производная постоянной равна нулю, т. е. С = 0.
Доказательство. Пусть у = С = const, тогда ∆у = 0. Следовательно,
![]() .
.
2. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же алгебраической сумме производных этих функций.
(U V) = U V .
Доказательство. Пусть у = U V. Зададим ∆х.
Новому значению х + ∆х аргумента соответствуют новые значения наших функций U + ∆U и V + ∆V. Тогда
∆y = ∆( U V) = [( U + ∆U) ( V + ∆V)] – ( U V) = ∆U ∆V,
Найдем
![]() .
.
3. Производная произведения конечного числа дифференцируемых функций равна
(U V) = V∙U + U∙V .
Доказательство. Пусть у = U V. Дадим х приращение ∆х.
Новому значению х + ∆х аргумента соответствуют новые значения функций U + ∆U, V + ∆V. Тогда функция U V получит приращение
∆y = ∆( U V) = [( U + ∆U) ( V + ∆V)] – U V =
= U V +V∆U + U ∆V+∆U∆V–UV = V∆U + U ∆V+∆U∆V.
По определению производной
![]()
![]()
При доказательстве
формулы надо учесть, что функция U
(x)
дифференцируема, и, следовательно,
непрерывна, т. е.
![]() .
.
4. Постоянный множитель можно выносить за знак производной, т. е.
(С∙у) = С у.
Доказательство. (Су) = Су + Су = Су.
5. Производная отношения двух функций равна
![]()
Доказательство.
![]() .
Составим ∆ у
.
Составим ∆ у
![]()
и найдем
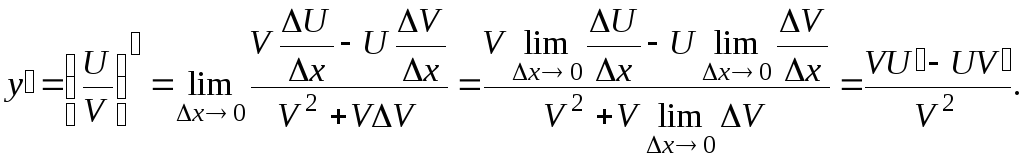
В доказательстве
формулы снова было учтено, что из
дифференцируемости функции V
(x)
следует ее непрерывность, т. е.
![]() .
.
6. Производная сложной функции. Пусть у = f (U), U = φ (x). Производная сложной функции f (φ (x)) равна произведению производной функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т. е.
![]()
где вместо U должно быть подставлено выражение U = φ (x). Коротко,
![]() .
.
7. Производная обратной функции. Производные от взаимно обратных функций обратные по величине
![]() или
или
![]() .
.
8. Производная функции, заданной параметрически. Пусть функция у (х) задана параметрическими уравнениями
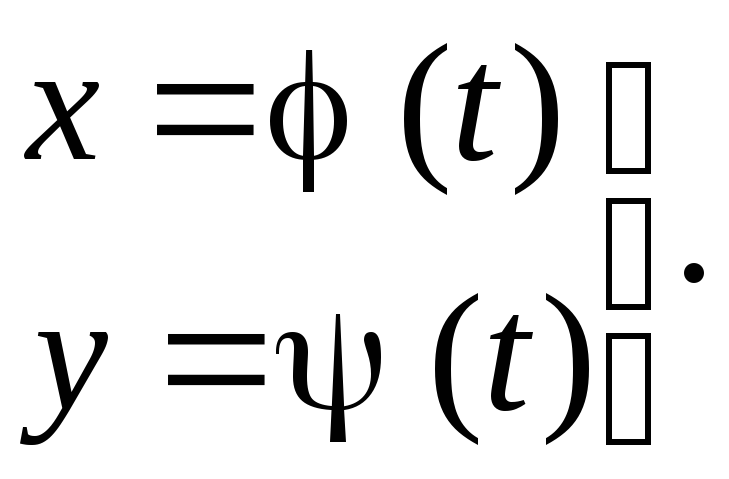
Дифференцируя у = ψ (t) по правилу дифференцирования сложной функции, получим
![]()
Производную
![]() найдем по правилу дифференцирования
обратной функции
найдем по правилу дифференцирования
обратной функции
![]()
Окончательно
![]() ,
что можно короче записать так
,
что можно короче записать так
![]() .
.
Производные основных элементарных функций
1.
![]() .
.
Найдем
![]()
Тогда
![]()
![]()
![]()
В частности
![]()
2. (xn) = n xn – 1.
Пусть
![]() Прологарифмируем обе части данного
выражения
Прологарифмируем обе части данного
выражения
![]() .
.
Продифференцируем обе части полученного равенства по отдельности, учитывая, что производная от ln y берется как от сложной функции:
![]()
3. (ax) = ax ln a.
Пусть
![]() Аналогично,
Аналогично,
![]()
![]()
![]()
В частности:
![]()
4. (sin x) = cos x.
Найдем
![]() Тогда
Тогда
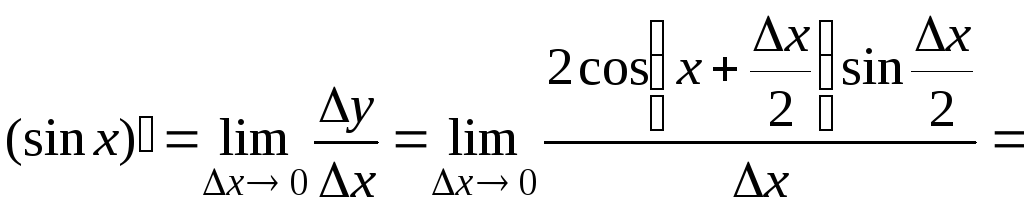
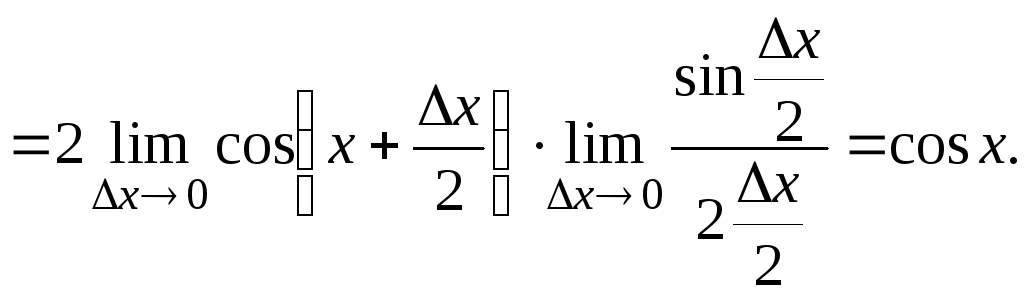
5. (cos x) = – sin x.
Так как
![]() то
то
![]()
6.
![]() Воспользуемся формулой нахождения
производной частного двух функций:
Воспользуемся формулой нахождения
производной частного двух функций:
![]()
7.
![]() Аналогично,
Аналогично,
![]()
![]()
8.
![]() .
Пусть y
= arcsin
x.
Тогда x
= sin
y
и
.
Пусть y
= arcsin
x.
Тогда x
= sin
y
и
![]() – по правилу нахождения производной
обратной функции.
– по правилу нахождения производной
обратной функции.
![]()
9.
![]() .
Пусть y
= arccos
х, тогда
x
= cos
y
и
.
Пусть y
= arccos
х, тогда
x
= cos
y
и
![]()
![]()
10.
![]() .
Пусть y
= arctg
x,
тогда x
= tg
y
и
.
Пусть y
= arctg
x,
тогда x
= tg
y
и
![]()
![]()
11.
![]() .
Пусть y
= arcctg
x,
тогда x
= ctg
y
и
.
Пусть y
= arcctg
x,
тогда x
= ctg
y
и
![]()
![]()
12. Логарифмическая производная.
![]()
а) Логарифмируя
функцию и дифференцируя полученное
равенство, получим
![]() .
Тогда
.
Тогда
![]()
13.
(sh
x)
= ch
x;
![]() – гиперболический синус.
– гиперболический синус.
![]() .
.
14.
(ch
x)
= sh
x;
![]() – гиперболический косинус.
– гиперболический косинус.
![]() .
.
15.
![]()
![]()
![]() – гиперболический тангенс.
– гиперболический тангенс.
![]() .
.
16.
![]()
![]()
![]() – гиперболический котангенс.
– гиперболический котангенс.
![]() .
.
