Решение практических задач по теме «Дифференциал функции одной переменной»

П р и м е р 14. Найти дифференциал функции .

Решение. Так как , то в данном случае

.

П р и м е р 15. Вычислить приближенно .

Решение. Воспользуемся приближенной формулой

.

Тогда, подставляя , получим

.

Полагая здесь х₀ = 1, ∆ х = 0, 02, найдем

.

Таким образом, .

П р и м е р 16. Найти предел по правилу Лопиталя.

Решение. Если в функцию подставить предельное значение х = 2, то получим неопределенность вида . Чтобы от нее избавиться необходимо применить правило Лопиталя, т. е.

Решение практических задач по теме «Исследование функции одной переменной»

П р и м е р 17. Исследовать функцию и построить ее график.

Решение. 1) Найдем область определения функции. Для этого знаменатель не должен равняться нулю, т. е.

.

Следовательно, D = (– , – 2)  (– 2; 2)  (2, + ).

2) Исследуем на четность и нечетность данную функцию. Для этого в функцию подставим вместо х значение (– х).

.

Так как у (– х)  у (х), но у (– х) = – у (х), то данная функция является нечетной.

Также данная функция не является периодической, т. к. у (х + Т)  у (х).

3) Исследуем поведение функции на концах области определения и односторонние пределы для точки х = 1.

,

,

,

,

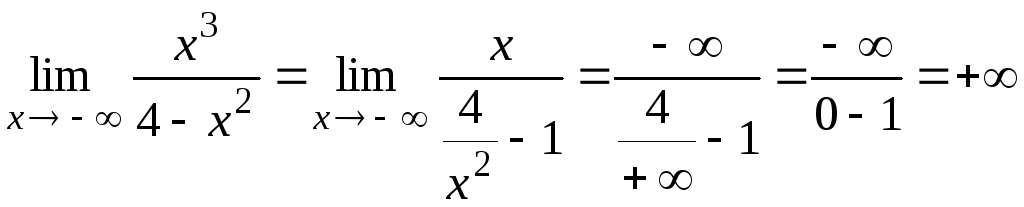
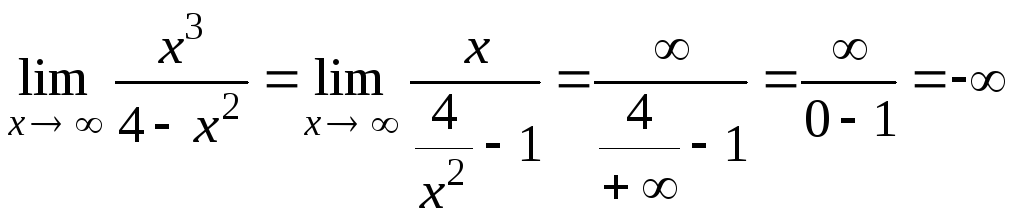
Значит х = 2 и х = – 2 – точки разрыва второго рода, т. е. вертикальные асимптоты.

4) Найдем горизонтальные или наклонные асимптоты в виде у = k x + b, где

.

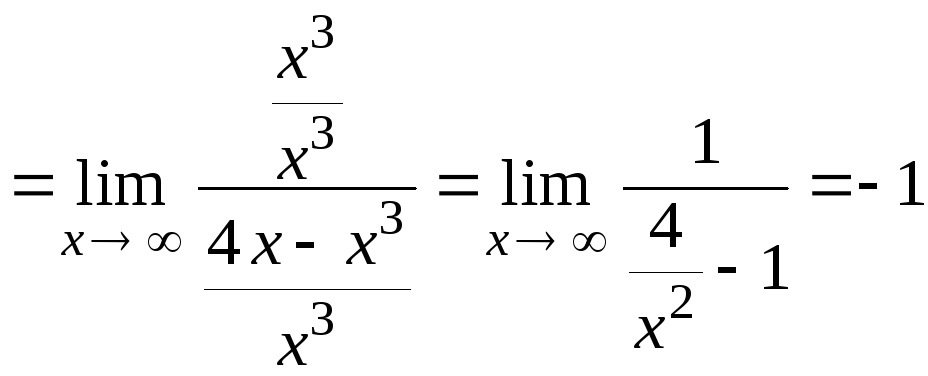Так как k  0, то горизонтальных асимптот у данной функции нет. Найдем значение b по формуле

.

Значит, наклонная асимптота имеет уравнение у = – x.

5) Найдем промежутки возрастания и убывания функции, а также точки экстремума, т. е. у  = 0:

,

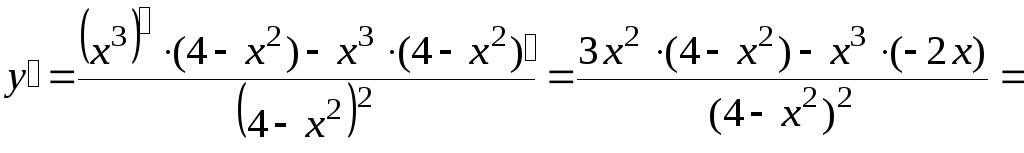
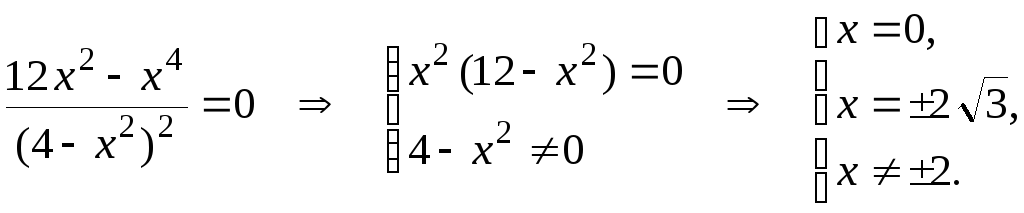
Составим таблицу, по которой найдем точки экстремума и промежутки возрастания и убывания.

х	(– ; )		(; – 2)	– 2	(– 2; 0)	0	(0; 2)	2	(2, )		(, +)
у (х)	+		+	–	–	0	+	–	–		–
у  (х)		0		–		0		–		0
		min		–		–		–		max

Значит на промежутках (– ; ), (, +) функция убывает, а на промежутках (; – 2), (– 2; 0), (0; 2) и (2, ) – возрастает.

6) Найдем промежутки выпуклости и вогнутости функции, а также точки перегиба, т. е. у  = 0:

,

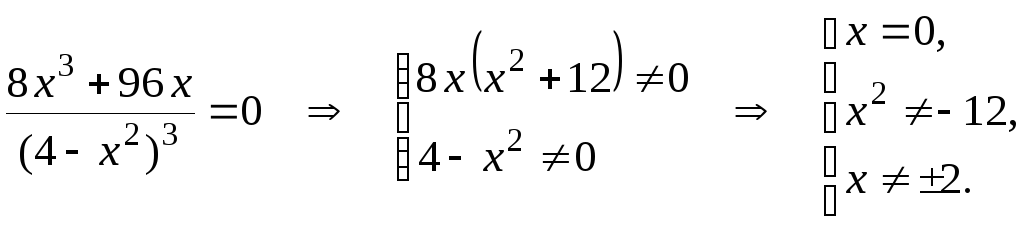
Составим таблицу, по которой найдем точки перегиба и промежутки выпуклости и вогнутости.

х	(– ; – 2)	– 2	(– 2; 0)	0	(0; 2)	2	(2; + )
у (х)	+	–	–	0	+	–	–
у  (х)	+	–	–	0	+	–	–
		–		пер.		–

Значит на промежутках (– ; – 2), (0; 2) функция выпукла, а на промежутках (– 2; 0), (2; + ) – вогнута.

7) Найдем точки пересечения с осями:

а) с осью Ох: у = 0. Тогда х = 0;

б) с осью Оу: х = 0. Тогда у = 0, т. е. график функции пересекает оси только в одной точке (0; 0).

8) Построим график данной функции (см. рис.).