
- •Глава 7 Дифференциальное исчисление функции одной переменной
- •§ 1. Производная функции одной переменной
- •Правила дифференцирования
- •§ 2. Дифференциал функции одной переменной
- •§ 3. Производные и дифференциалы высших порядков
- •§ 4. Правило Лопиталя (1661 – 1704)
- •§ 5. Исследование функции одной переменной
- •Решение практических задач по теме «Производная функции одной переменной»
- •Решение практических задач по теме «Дифференциал функции одной переменной»
- •Решение практических задач по теме «Исследование функции одной переменной»
- •Примеры для самостоятельного решения.
§ 4. Правило Лопиталя (1661 – 1704)
Т е о р е м а
11.
(раскрытие
неопределенности вида
![]() ).
Пусть функции f1(x)
и f2(x)
определены и дифференцируемы в точке
а
и некоторой ее окрестности (хотя бы
односторонней) и
).
Пусть функции f1(x)
и f2(x)
определены и дифференцируемы в точке
а
и некоторой ее окрестности (хотя бы
односторонней) и
![]() ,
,
а f
2(x)
0 в указанной окрестности. Тогда, если
существует предел отношения производных
![]() (конечный или бесконечный), то существует
и
(конечный или бесконечный), то существует
и
![]() ,
причем
,
причем
![]() .
.
Эту теорему называют правилом Лопиталя.
Доказательство.
Пусть существует
![]() ,
тогда
,
тогда
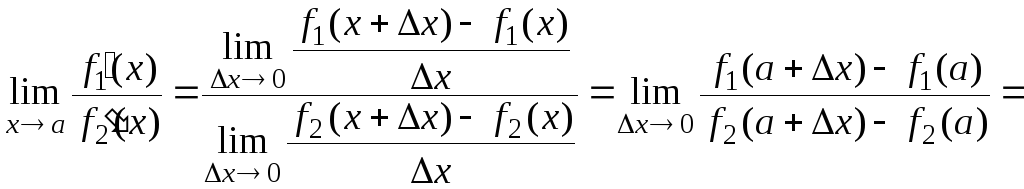
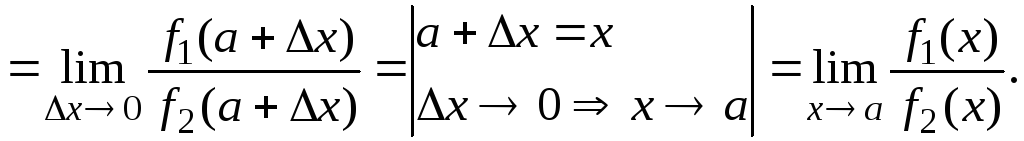
Что и требовалось доказать.
Следствие.
Правило Лопиталя справедливо и для
неопределенности вида
![]() ,
т. е. когда
,
т. е. когда
f1(x) → , f2(x) → при х → а.
Доказательство.

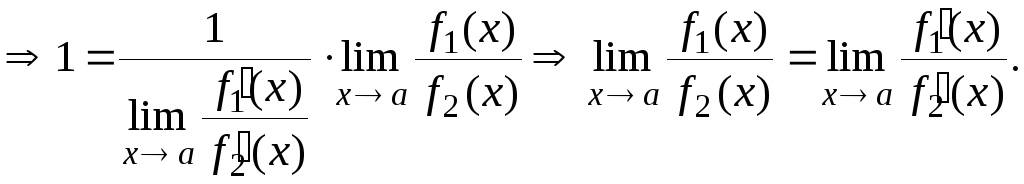
Замечание. Если относительно производных f 1(x) и f 2(x) продолжает сохраняться неопределенность, то правило Лопиталя применяют повторно.
Другие виды неопределенностей и их раскрытие
Правило Лопиталя
применяется для раскрытия неопределенностей
вида
![]() ,
которые называют основными.
,
которые называют основными.
Неопределенности вида:
а) 0∙, б) – , в) 00, г) 0, д) 1
сводятся к двум основным видам путем тождественных преобразований.
а)
Пусть
![]() ,
,
![]() .
Требуется найти
.
Требуется найти
![]() .
Это неопределенность вида 0∙.
Можно искомое выражение переписать в
виде
.
Это неопределенность вида 0∙.
Можно искомое выражение переписать в
виде

или
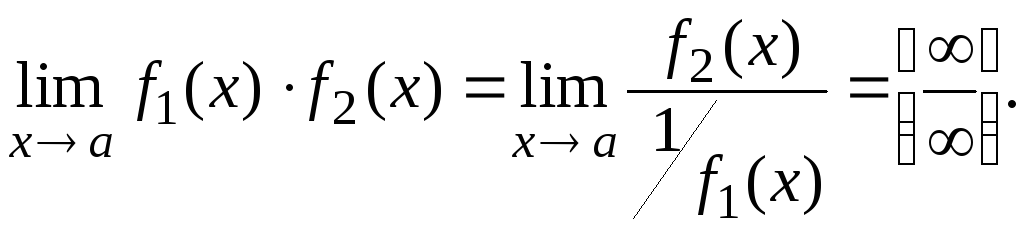
б)
Пусть
![]() ,
,
![]() .
Требуется найти
.
Требуется найти
![]() .
Это неопределенность вида
– .
.
Это неопределенность вида
– .
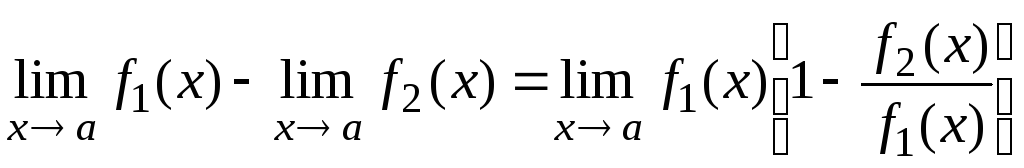 .
.
В результате получаем либо определенность, либо неопределенность вида ∙0.
в)
Пусть
![]() ,
,
![]() .
Требуется найти
.
Требуется найти
![]() .
Это неопределенность вида 00.
.
Это неопределенность вида 00.
Положив
![]() нужно прологарифмировать обе части
полученного равенства:
нужно прологарифмировать обе части
полученного равенства:
![]() .
.
Получим
неопределенность типа 0∙.
Вычислив
![]() ,
легко получить
,
легко получить
![]() ,
т. е.
,
т. е.
![]() ,
,
и если
![]() ,
то
,
то
![]() .
.
Аналогичным приемом находятся пределы и в случае г), д).
§ 5. Исследование функции одной переменной
Т е о р е м а 12. (о постоянстве функции на отрезке). Если функция f (x) непрерывна на отрезке [a, b] и имеет во всех его внутренних точках производную f (x) = 0, то функция постоянна на отрезке [a, b].
Следствие. Если производные двух функций φ (х) и g (x) равны во всех точках отрезка [a, b], то разность этих функций постоянна на этом отрезке.
Т е о р е м а 13. (достаточное условие возрастания функции). Если непрерывная на отрезке [a, b] функция у = f (x) в каждой внутренней точке этого отрезка имеет положительную производную, то эта функция возрастает на отрезке [a, b].
Доказательство. Пусть f (x) > 0 для всех х ∈ (a, b). Рассмотрим два произвольных значения х1 и х2 из [a, b], причем х1 < х2. Напишем формулу Лагранжа применительно к отрезку [х1, х2]:
f (x2) – f (x1) = (x2 – x1)∙f (c), с ∈ (х1, х2).
По условию теоремы f (с) > 0, т. к. х1 < х2, то и (х2 – х1) > 0. Тогда произведение
(х2 – х1)∙ f (с) > 0
и, следовательно,
f (x2) – f (x1) > 0.
Отсюда f (x2) > f (x1), т. е. f (x) возрастает на отрезке [a, b]. Что и требовалось доказать.
Подобным же образом доказывается следующая теорема.
Т е о р е м а 14. (достаточное условие убывания функции). Если непрерывная на отрезке [a, b] функция у = f (x) в каждой внутренней точке этого отрезка имеет отрицательную производную, то эта функция убывает на отрезке [a, b].
Определение10. Функция у = f (x) имеет максимум в точке х = с, если существует такая окрестность точки х = с, что для всех точек х с из этой окрестности, выполняется неравенство f (с) > f (x).
Функция у = f (x) имеет минимум в точке х = с, если существует такая окрестность точки х = с, что для всех точек х с из этой окрестности, выполняется неравенство f (с) < f (x).
Максимум и минимум объединяются общим названием экстремум функции.
Геометрическое истолкование.
З начения
функций f
(с1)
и f
(с3)
больше значений функции во всех «соседних»
точках как слева, так и справа от с1
и с3
соответственно, следовательно в точках
с1
и с3
функция f
(х)
имеет максимум.
начения
функций f
(с1)
и f
(с3)
больше значений функции во всех «соседних»
точках как слева, так и справа от с1
и с3
соответственно, следовательно в точках
с1
и с3
функция f
(х)
имеет максимум.
Аналогично, значение функций f (с2) и f (с4) меньше значений функции во всех «соседних» точках как слева, так и справа от с2 и с4 соответственно, следовательно в точках с2 и с4 функция f (х) имеет минимум.
Следует отметить, что если функция имеет в точке максимум или минимум, то это не означает, что в этой точке функция имеет наибольшее или наименьшее значение во всей области ее определения. Из определения максимума (минимума) следует только то, что это самое большее (меньшее) значение функции в точках, достаточно близких к точке с.
Нетрудно видеть, что функция, изображенная на рисунке имеет наименьшее значение в точке с2, а наибольшее в точке х = b, т. е.
fнаим = f (с2) , fнаиб = f (b).
Может оказаться, что минимум функции больше чем максимум:
fmax(c1) < fmin(c4).
Т е о р е м а 15. (необходимый признак существования экстремума функции). Если дифференцируемая в точке х = с функция у = f (x) имеет в этой точке экстремум, то ее производная при х = с обращается в ноль, т. е. f (с) = 0.
Доказательство. Пусть, для определенности, функция у = f (x) имеет в точке с максимум. Согласно определению максимума, должна существовать такая окрестность точки с, что для любого х (х с) этой окрестности
f (с) > f (x),
т. е. f (с) – наибольшее значение функции в этой окрестности. Так как по условию функция имеет в точке с производную f (с), то по теореме Ферма
f (с) = 0.
А налогично
доказывается теорема и для случая
минимума функции.
налогично
доказывается теорема и для случая
минимума функции.
З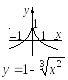 амечание.
Функция может достигать экстремума,
так же в точке, в которой производная
не существует. Например, у
= |x|
не имеет производной в точке х
= 0, но достигает в ней минимума. Функция
амечание.
Функция может достигать экстремума,
так же в точке, в которой производная
не существует. Например, у
= |x|
не имеет производной в точке х
= 0, но достигает в ней минимума. Функция
![]() ,
не имеет в точке х
= 0 производной, но достигает в ней
максимума.
,
не имеет в точке х
= 0 производной, но достигает в ней
максимума.
![]()
С л е д с т в и е. Если непрерывная функция у = f (x) имеет в точке х = с экстремум, то производная f (с) обращается в ноль или не существует.
Определение 11. Значения аргумента, при которых производная обращается в ноль или терпит разрыв, будем называть стационарными или критическими точками функции (точки подозрительные на экстремум).
Замечание. Не всякая стационарная точка является точкой экстремума, т. е. условие того, что у = 0 не является достаточным условием существования экстремума. Так, например, функция у = х3 в точке х = 0 имеет f (0) = 0:
у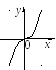
= 3 х2
= 0, следовательно х
= 0,
= 3 х2
= 0, следовательно х
= 0,
х = 0 – стационарная точка. Однако в этой точке функция не имеет экстремума. Действительно, как бы ни была близка точка х к точке О, всегда х3 < 0 при х < 0 и х3 > 0 при х > 0.
Т е о р е м а 16. (первый достаточный признак существования экстремума). Если производная функции f (x) при переходе аргумента слева направо через критическую точку х = с меняет знак с плюса на минус, то функция в точке с имеет максимум, а при перемене знака с минуса на плюс – минимум, т. е. если f (с) = 0 и
– при
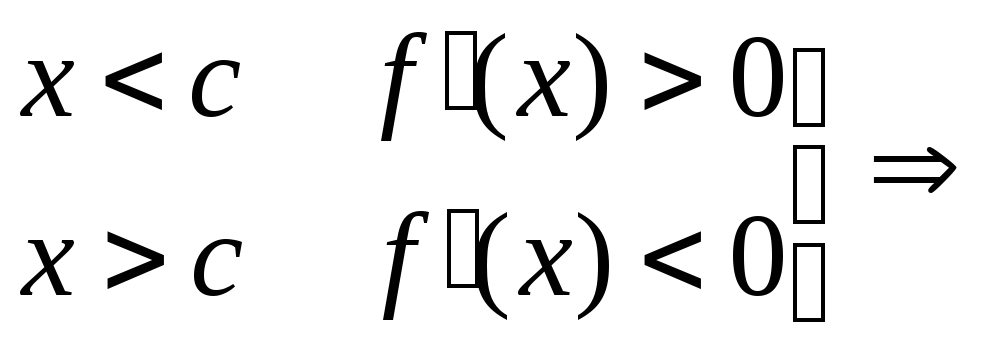 f
(c)
–максимум;
f
(c)
–максимум;
– при
 f
(с)
– минимум.
f
(с)
– минимум.
Замечание. Если производная f (x) не меняет знака при переходе через критическую точку, то функция в этой точке не имеет ни максимума, ни минимума.
Т е о р е м а 17. (второй достаточный признак существования экстремума). Пусть f (с) = 0. Тогда, если f (с) < 0, то в точке х = с функция имеет максимум; если f (с) > 0, то в точке х = с функция имеет минимум.
Определение 12. График функции у = f (x) называется выпуклым вверх (выпуклым) в интервале (а, b), если он расположен ниже любой своей касательной на этом интервале.
График функции у = f (x) называется выпуклым вниз (вогнутым) в интервале (а, b), если он расположен выше любой своей касательной на этом интервале.

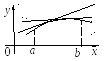
График выпуклый График вогнутый
Т е о р е м а 18. (достаточный признак выпуклости (вогнутости) графика функции). Пусть у = f (x) имеет вторую производную во всех точках интервала (а, b). Если во всех точках этого интервала f (х) < 0, то график функции в этом интервале выпуклый, если же f (х) > 0, – вогнутый.
Определение 13. Точка графика, при переходе через которую график функции у = f (x) меняет характер выпуклости, называется точкой перегиба.
Нахождение точек перегиба графика функции основано на следующих теоремах.
Т е о р е м а 19. (достаточный признак существования точки перегиба). Если вторая производная f (х) меняет знак при переходе через точку х0, то точка с абсциссой х = х0 является точкой перегиба графика функции.
Д оказательство.
Пусть, например, f
(х)
<
0 при x
< x0
и f
(х)
> 0 при x
> x0.
В этом случае слева от точки х0
график выпуклый, а справа от точки х0
– вогнутый.
оказательство.
Пусть, например, f
(х)
<
0 при x
< x0
и f
(х)
> 0 при x
> x0.
В этом случае слева от точки х0
график выпуклый, а справа от точки х0
– вогнутый.
Следовательно, при переходе через точку х0 график у = f (x) меняет характер выпуклости. Тогда по определению точка х0 является точкой перегиба.
Т е о р е м а 20. (необходимый признак существования точки перегиба). Пусть функция у = f (x) имеет в интервале (а, b) непрерывную производную f (х). Тогда, если точка с абсциссой x0 ∈ (а, b) является точкой перегиба графика данной функции, то f (х0) = 0.
Доказательство. Пусть х0 – точка перегиба с выпуклости на вогнутость, тогда f (х) < 0 при х < х0 и f (х) > 0 при х > х0. Тогда по первому достаточному признаку существования экстремума (теорема 5) х = х0 – точка минимума функции f (х). Следовательно, по необходимому условию существования экстремума (теорема 4) f (х0) = 0.
Рассмотрим рисунки:

Определение 14. Асимптотой графика функции у = f (x) называется прямая линия, обладающая тем свойством, что расстояние от переменной точки на графике до прямой стремится к нулю при неограниченном удалении этой точки по графику от начала координат (см. примеры на рис. выше).
Классификация асимптот: наклонная (не параллельна ни одной из осей координат), горизонтальная (параллельна оси Ох), вертикальная (параллельна оси Оу).
Правило нахождения наклонной и горизонтальной асимптот
Т е о р е м а 21. (о параметрах асимптот). Если y = k∙x + b – уравнение асимптоты кривой у = f (x), то
![]()

![]() .
.
С л е д с т в и е. Если k = 0, а b – конечное число, то график у = f (x) будет иметь горизонтальную асимптоту у = b.
Замечания. 1) Если хотя бы один из пределов теоремы 21 не существует, то график у = f (x) не имеет асимптоты при х → + .
2) Аналогично находятся асимптоты при х → – . Пределы теоремы 21 при х → + и при х → – могут быть различными.
3) Формулы в теореме 21 годятся лишь для нахождения наклонных и горизонтальных асимптот. Вертикальные асимптоты имеют уравнение х = а. Эта прямая является асимптотой, если в точке х = а график функции терпит бесконечный разрыв, т. к. точка х = а является точкой разрыва второго рода. Для уточнения поведения функции в окрестности точки разрыва необходимо вычислить односторонние пределы в этой окрестности.
