
- •Предисловие
- •§ 1. Взаимно однозначное соответствие между множествами. Эквивалентные множества
- •Дополнительные задания
- •§ 2. Счетные множества
- •Дополнительные задания
- •§3. Мощность множества. Множества мощности континуума
- •Дополнительные задания
- •§4.Понятие метрического пространства
- •Дополнительные задания
- •§ 5. Замкнутые и открытые множества в метрических пространствах
- •Дополнительные задания
- •§ 6. Сходимость в метрических пространствах
- •Дополнительные задания
- •§ 7. Отображения метрических пространств. Непрерывность отображений
- •Дополнительные задания
- •§ 8. Компактные множества в метрических пространствах
- •Дополнительные задания
- •§ 9. Полные метрические пространства
- •Дополнительные задания
- •§ 10. Принцип сжимающих отображений
- •Дополнительные задания
- •§ 11. Измеримые множества
- •Дополнительные задания
- •§ 12. Функции, измеримые по Лебегу
- •Дополнительные задания
- •§ 13. Интеграл Лебега. Сравнение интегралов Римана и Лебега
- •Дополнительные задания
§ 13. Интеграл Лебега. Сравнение интегралов Римана и Лебега
Литература: [1], глава II, §§ 1-3.
Задачи этого параграфа позволят студенту глубже усвоить определение понятия интеграла Лебега, его свойства; понять связь между интегралами Римана и Лебега; научиться вычислять интегралы Лебега.
Содержание задач связано с материалом предыдущих параграфов, что дает возможность повторить такие понятия, как мера множества, измеримая функция, канторово множество и др.
-
Покажите, пользуясь определением, что функция
 ,
определенная и ограниченная на множестве
,
определенная и ограниченная на множестве
 нулевой меры, интегрируема по Лебегу
на
нулевой меры, интегрируема по Лебегу
на
 и
и
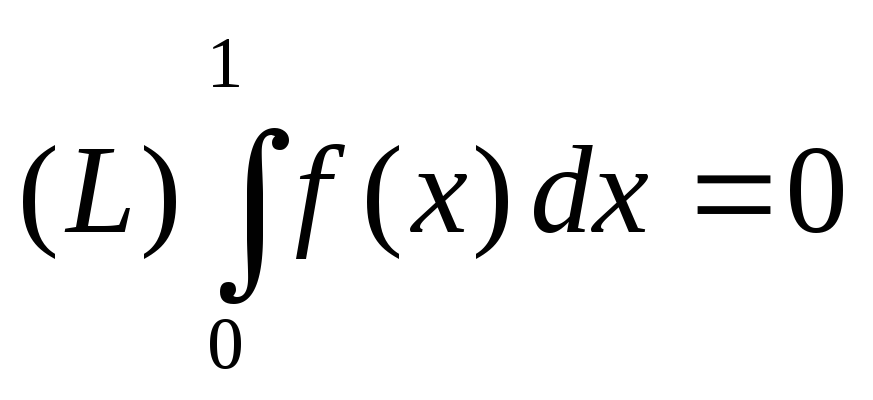 .
. -
Покажите, пользуясь определением, что функция
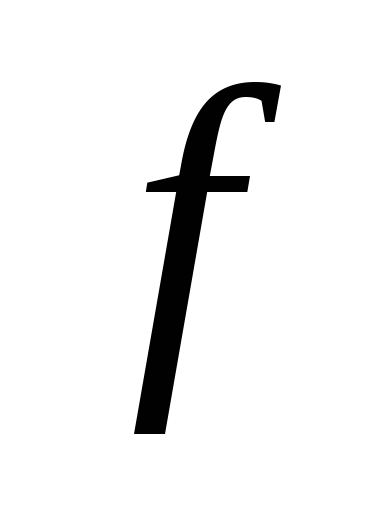 ,
принимающая постоянное значение
,
принимающая постоянное значение
 на измеримом множестве
на измеримом множестве
 ,
интегрируема на
,
интегрируема на
 ,
и
,
и
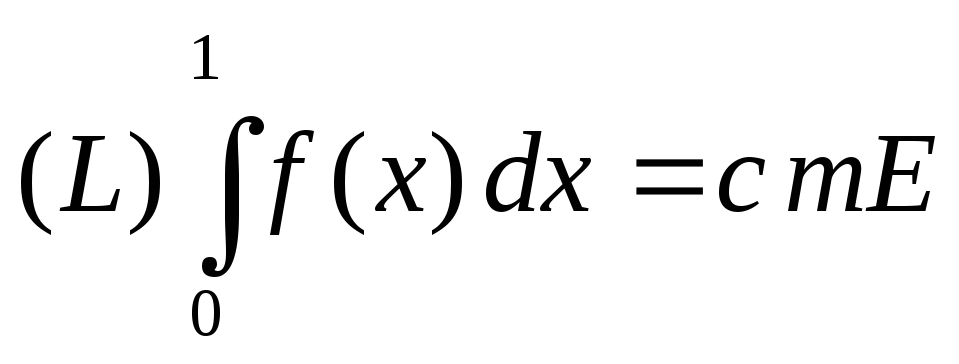 .
. -
Пусть функция
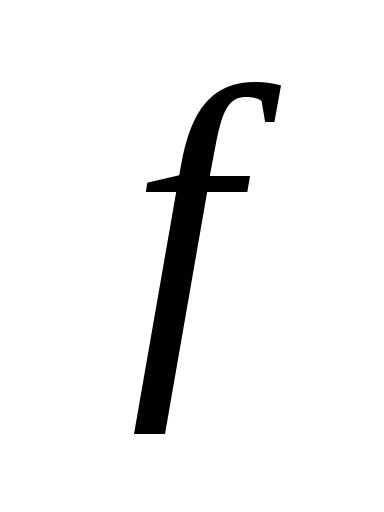 ограничена и измерима на множестве
ограничена и измерима на множестве
 .
Докажите, что
.
Докажите, что
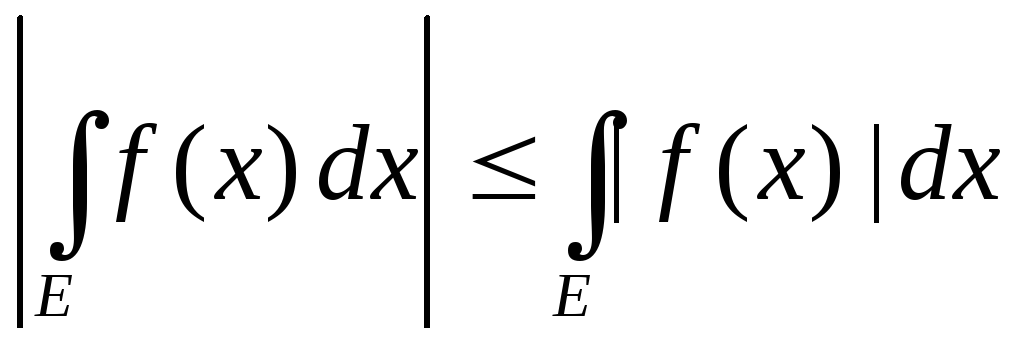 .
. -
Докажите, что функция Дирихле
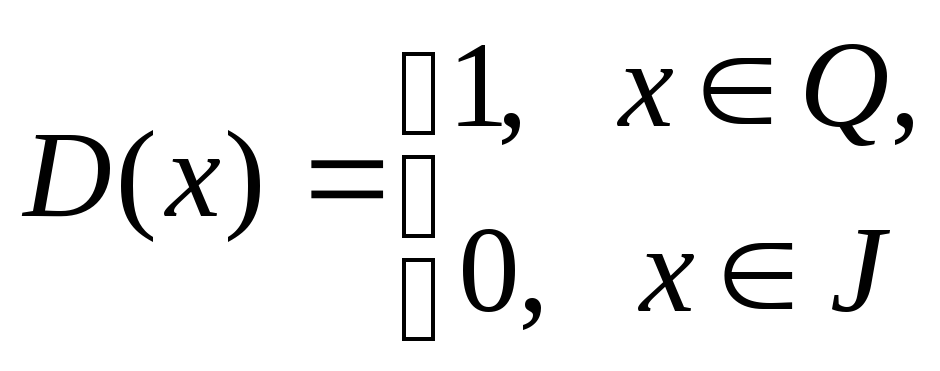 не интегрируема по Риману на отрезке
не интегрируема по Риману на отрезке
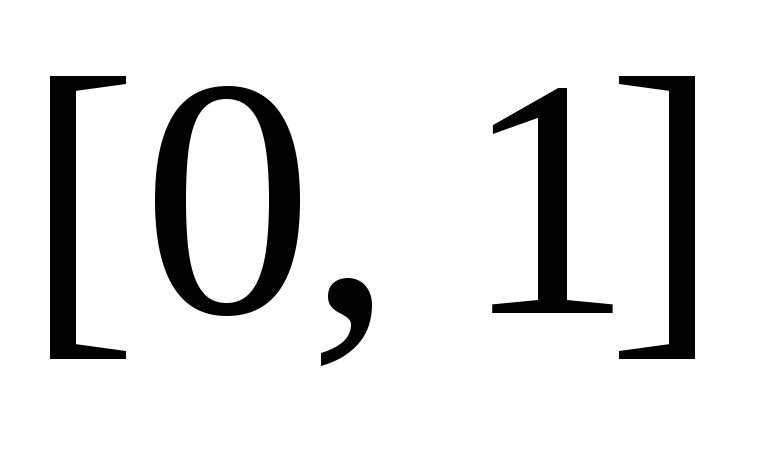 ,
но интегрируема по Лебегу на этом
множестве и
,
но интегрируема по Лебегу на этом
множестве и
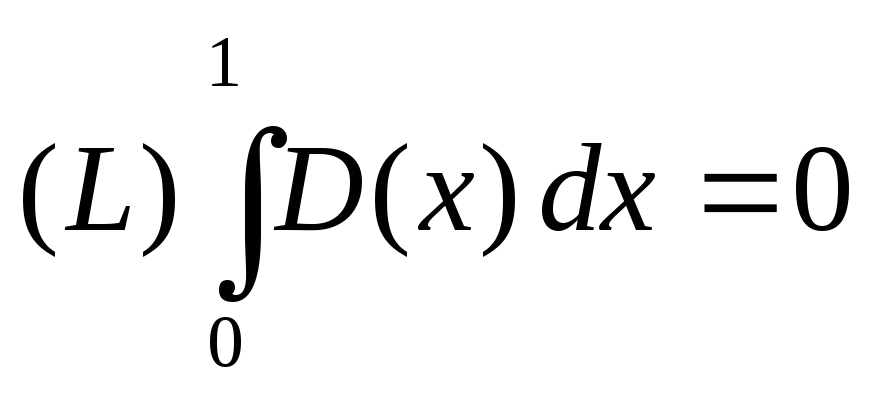 .
. -
Выясните, интегрируема ли функция
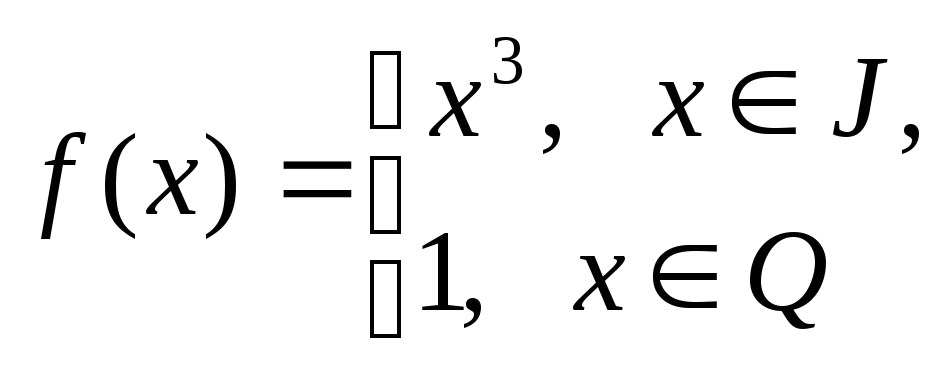 по Лебегу на отрезке
по Лебегу на отрезке
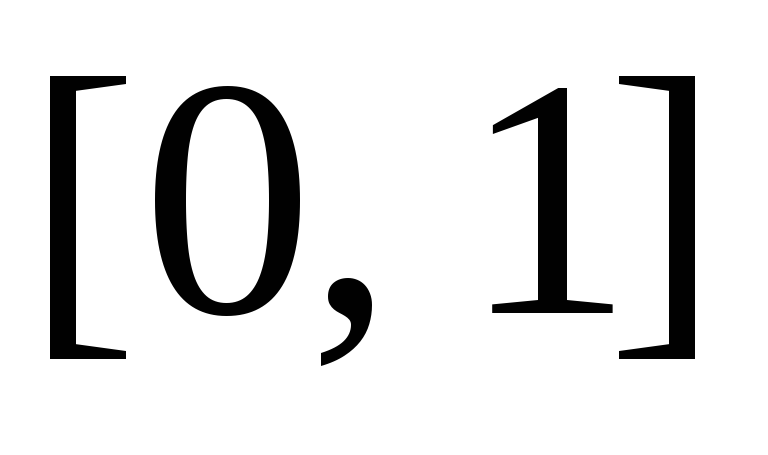 .
Чему равен интеграл
.
Чему равен интеграл


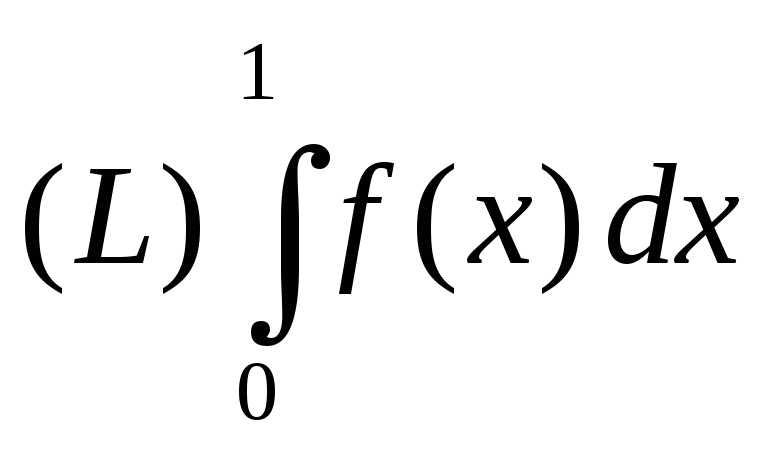 ?
? -
Выясните, интегрируема ли функция
 по Риману на отрезке
по Риману на отрезке
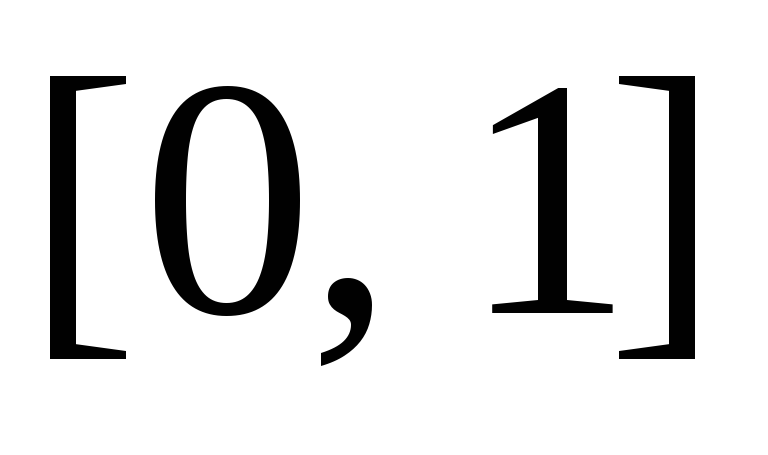 .
Если да, то вычислите
.
Если да, то вычислите


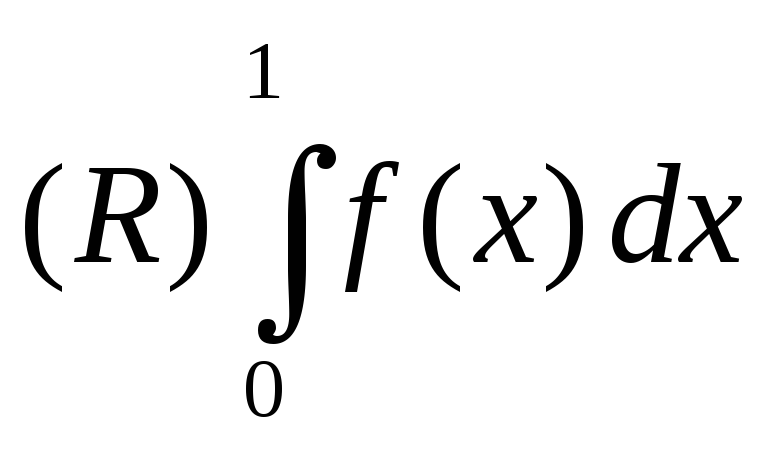 .
. -
Докажите, что функция
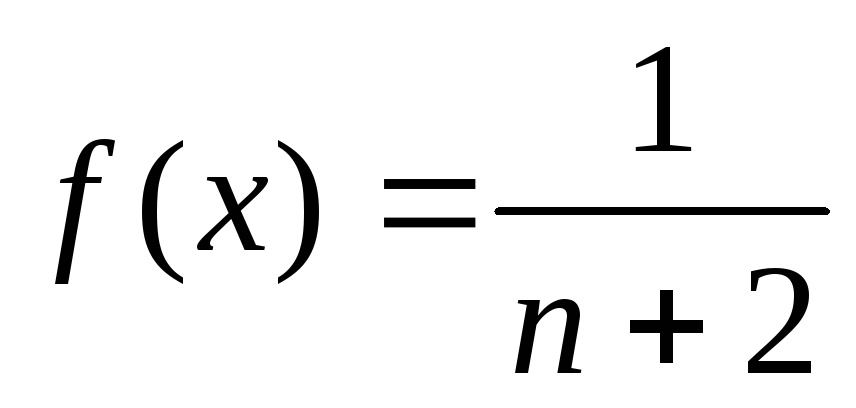 при
при
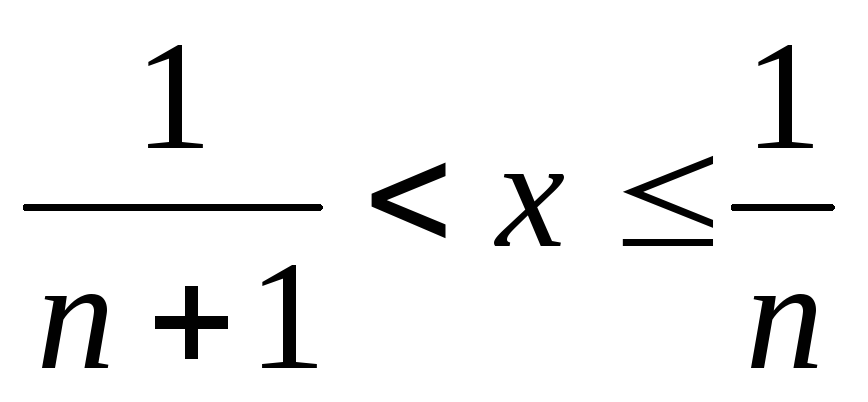 интегрируема на отрезке
интегрируема на отрезке
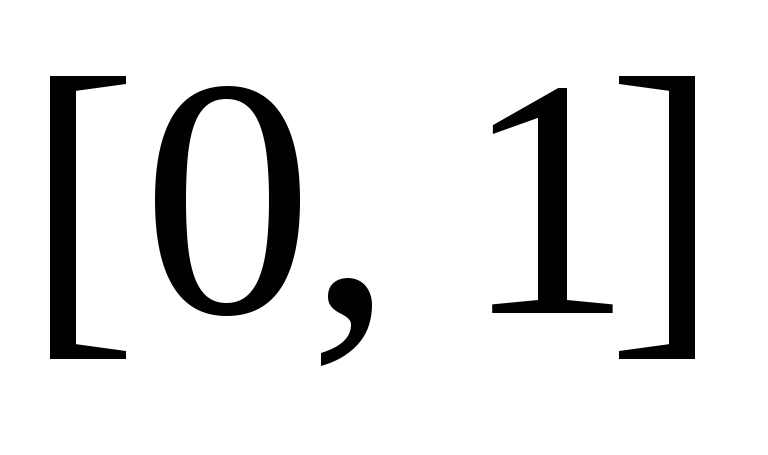 по Лебегу, и найдите интеграл.
по Лебегу, и найдите интеграл. -
Выясните, интегрируема ли по Лебегу функция
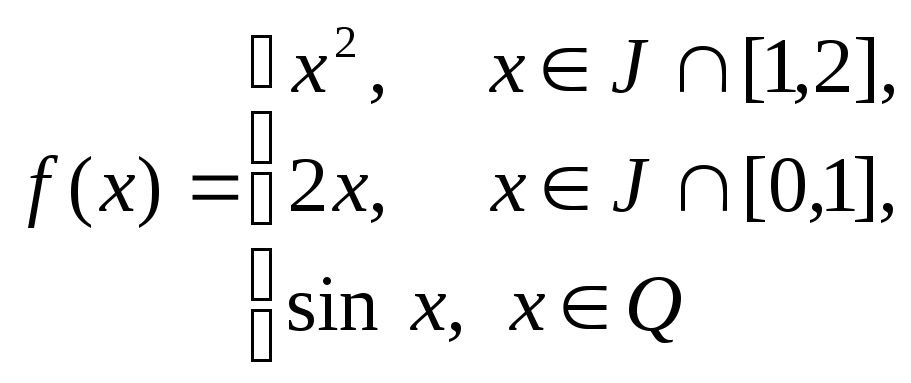 на отрезке
на отрезке
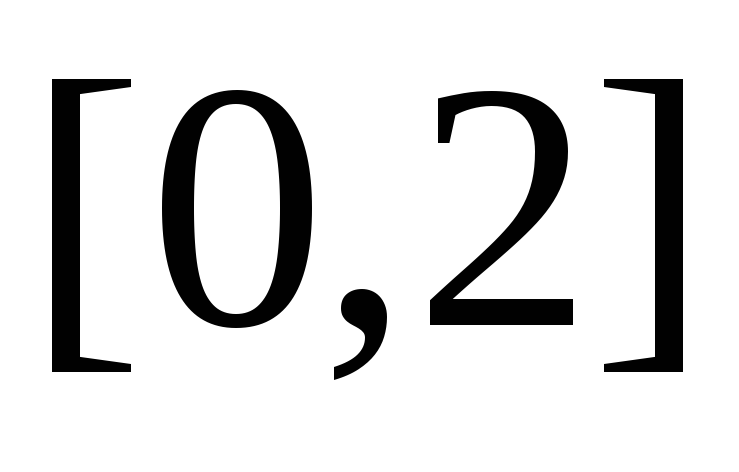 ?
? -
Докажите, опираясь на свойства интеграла Лебега, что
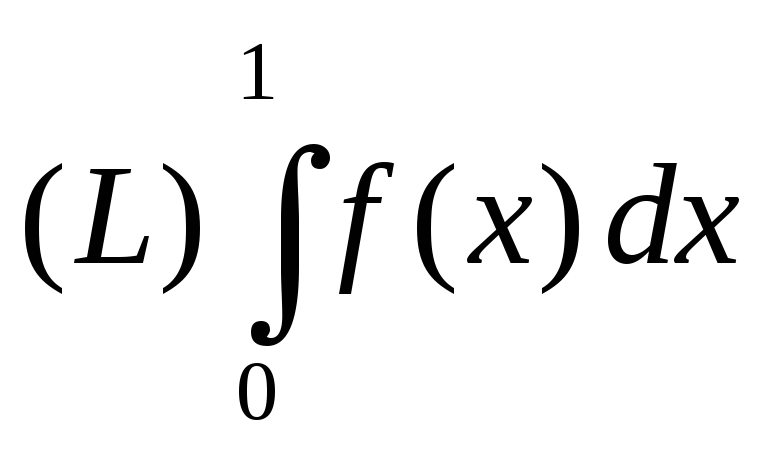 существует и вычислите его, если:
существует и вычислите его, если:
а)
![]()
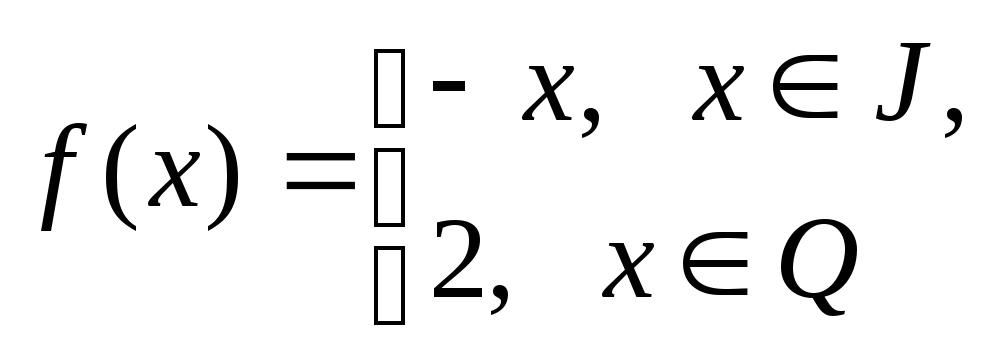 ; б)
; б)
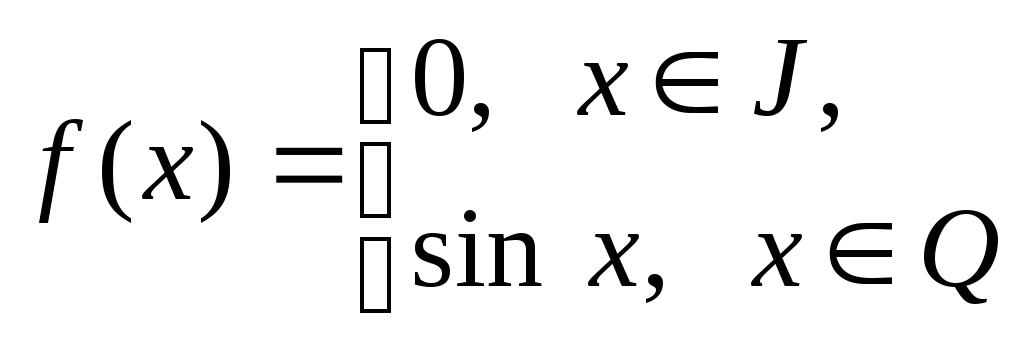 ;
;
в)
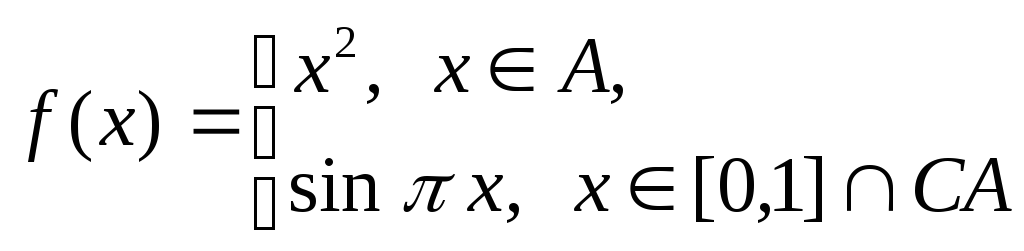 ,
где
,
где
![]() – множество алгебраических чисел из
– множество алгебраических чисел из
![]() ,
а
,
а
![]() ;
;
г)
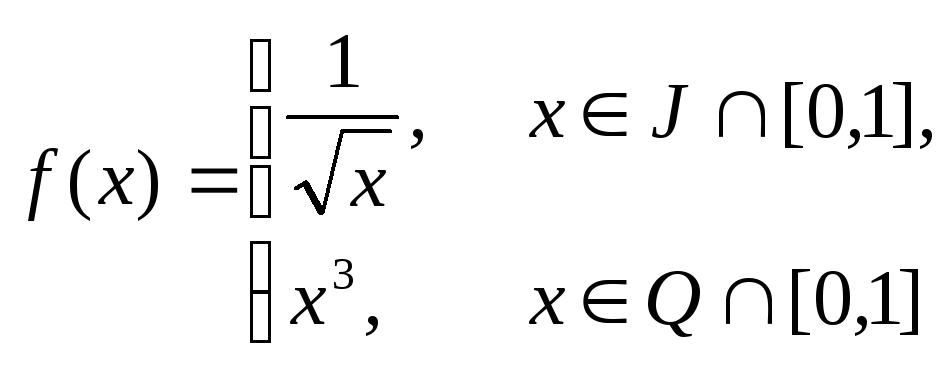 .
.
-
Докажите, что функция
 ,
равная 0 на канторовом множестве
,
равная 0 на канторовом множестве
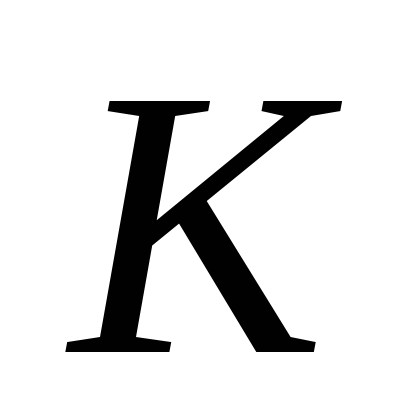 и 2 в остальных точках отрезка
и 2 в остальных точках отрезка
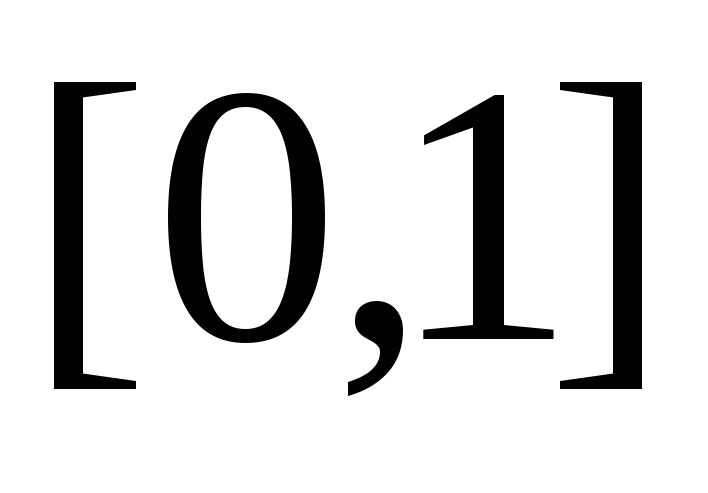 ,
интегрируема по Лебегу на этом отрезке.
Вычислите интеграл.
,
интегрируема по Лебегу на этом отрезке.
Вычислите интеграл. -
Докажите, что следующие функции интегрируемы по Лебегу на отрезке
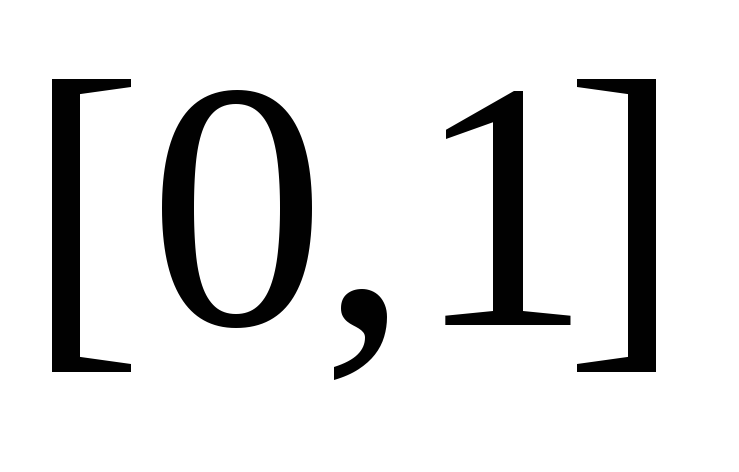 и вычислите интегралы:
и вычислите интегралы:
а)
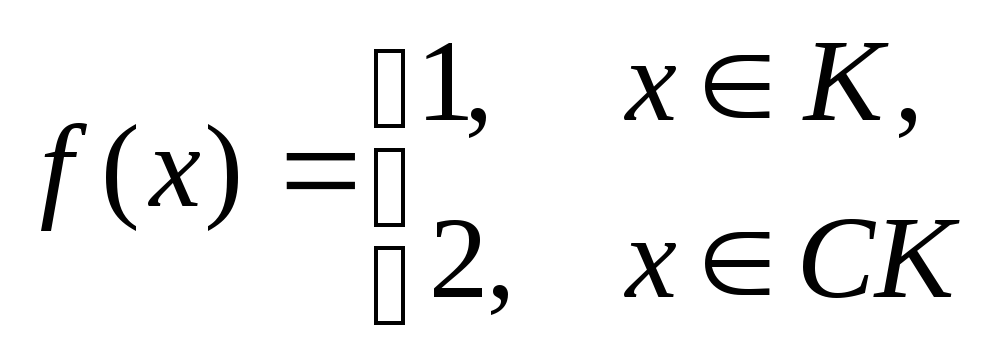 ,
где
,
где
![]() – канторово множество, а
– канторово множество, а
![]() – его дополнение до всего отрезка
– его дополнение до всего отрезка
![]() ;
;
б)
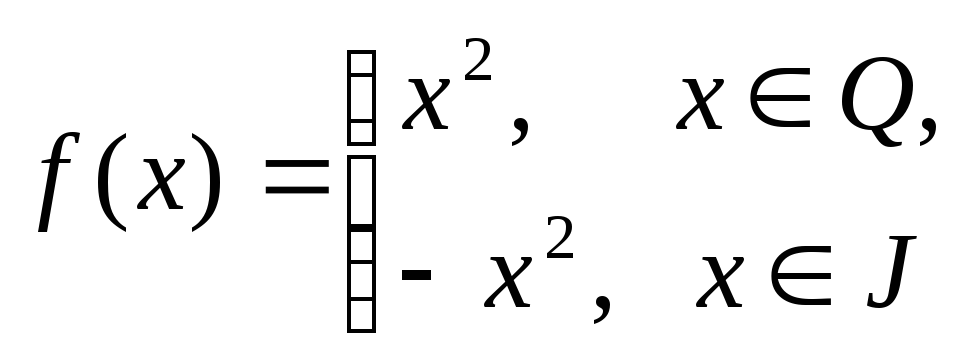 ;
;
в)
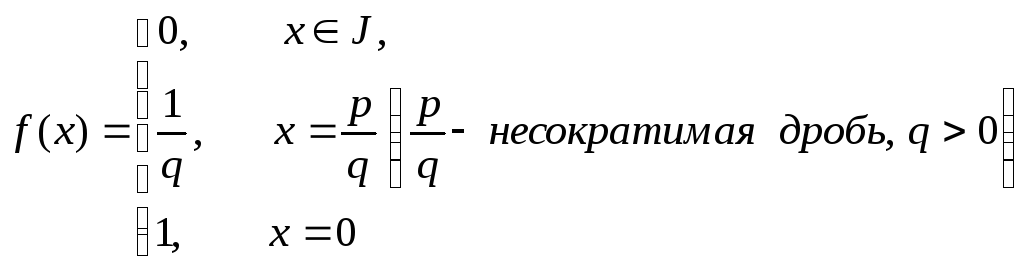 .
.
13.231. Вычислить
интеграл Лебега от функции
![]() на отрезке
на отрезке
![]() ,
если
,
если
![]() в точках
в точках
![]() – дополнения канторова множества до
отрезка
– дополнения канторова множества до
отрезка
![]() ,
а на смежных интервалах канторова
множества
,
а на смежных интервалах канторова
множества
![]() графиком функции служат верхние
полуокружности, опирающиеся на эти
интервалы, как на диаметры.
графиком функции служат верхние
полуокружности, опирающиеся на эти
интервалы, как на диаметры.
-
Множество
 получено из отрезка
получено из отрезка
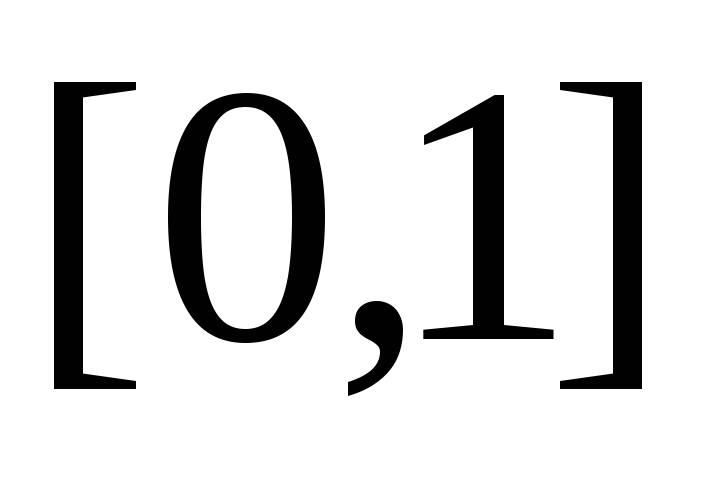 удалением интервалов
удалением интервалов
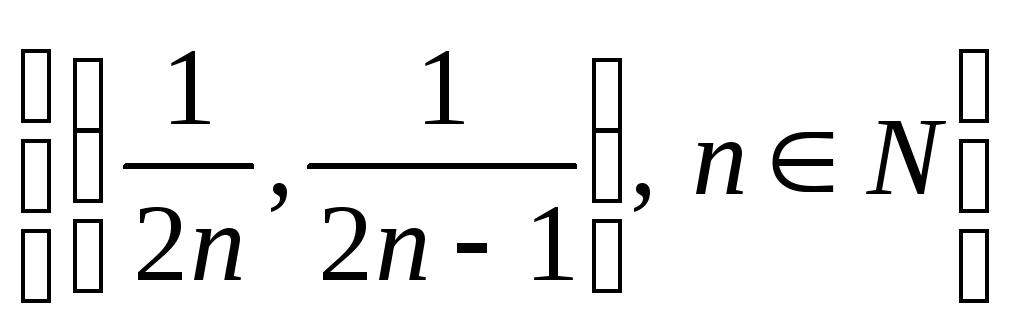 .
Покажите, что функция
.
Покажите, что функция
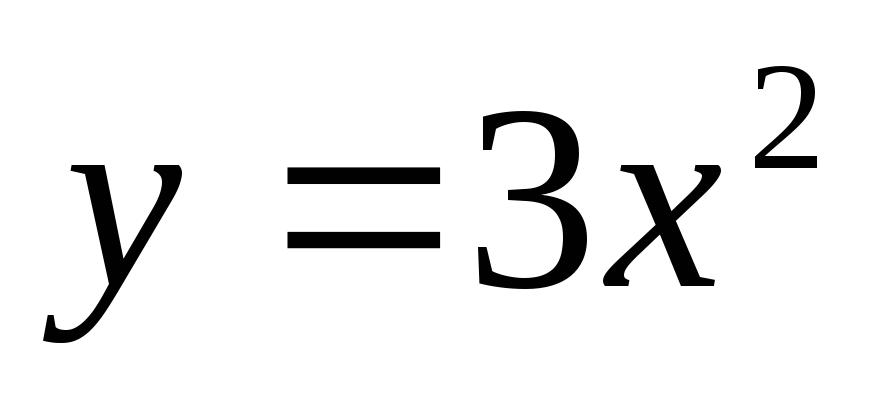 интегрируема по Лебегу на множестве
интегрируема по Лебегу на множестве
 .
. -
Вычислите
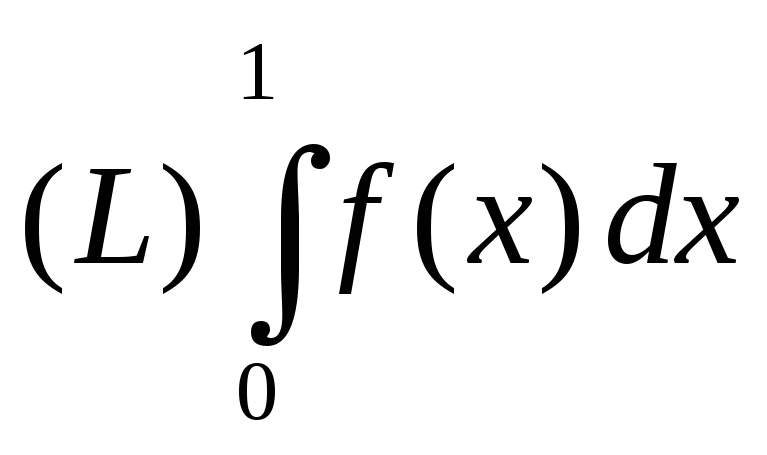 ,
если
,
если
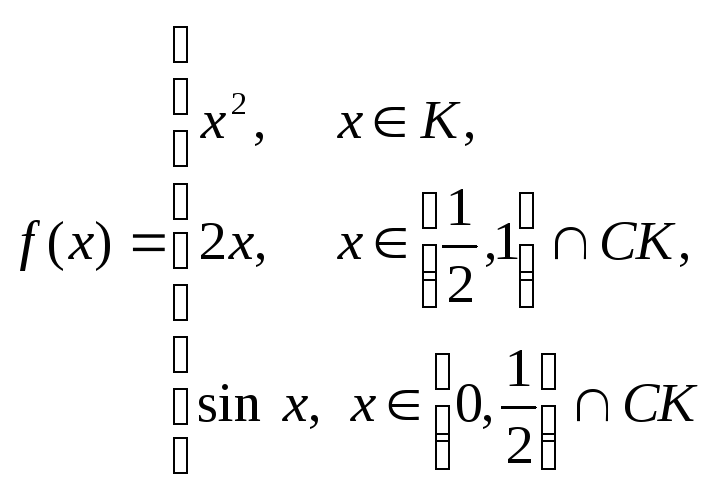 ,
где
,
где
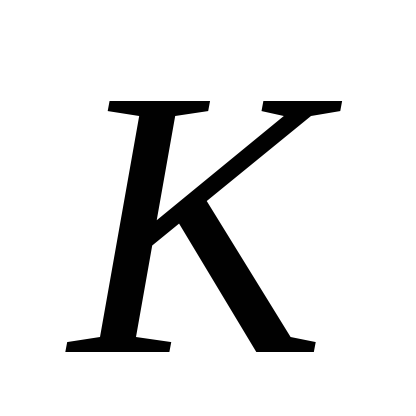 – канторово множество, а
– канторово множество, а
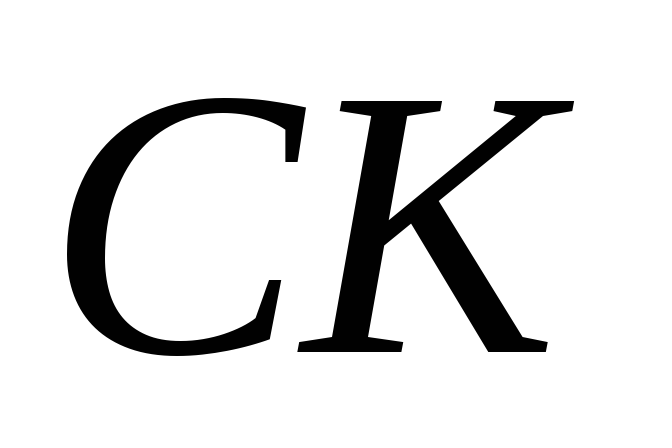 – его дополнение до всего отрезка
– его дополнение до всего отрезка
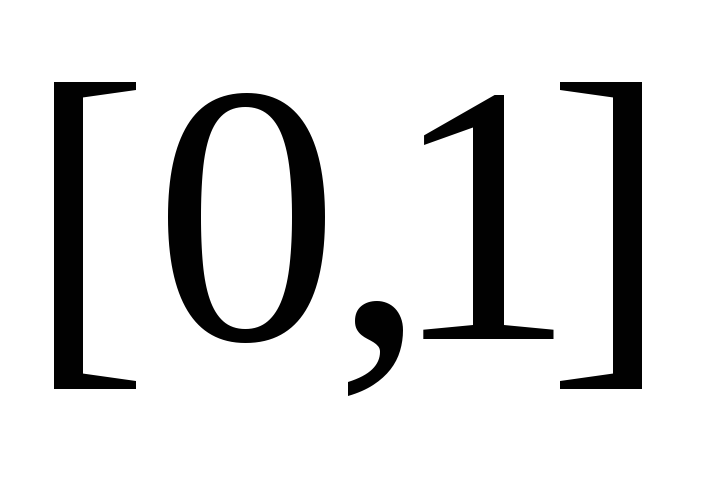 .
.
Дополнительные задания
-
Покажите, что если
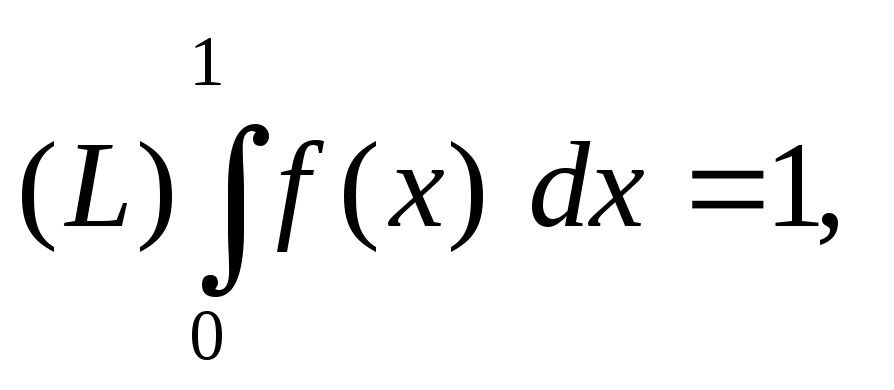 где
где
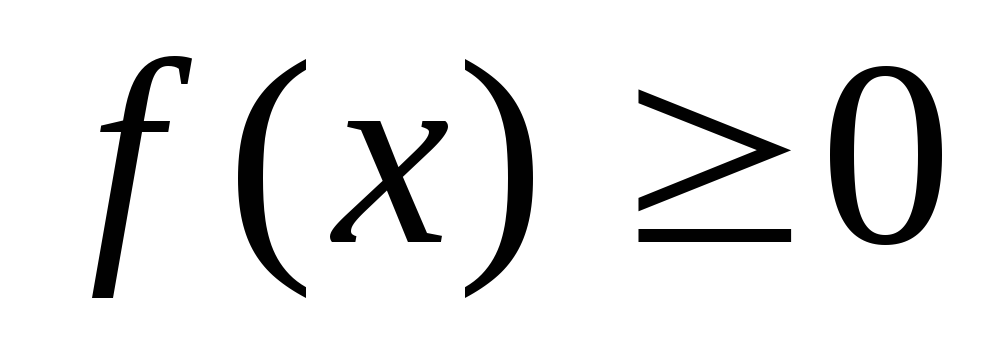 на
отрезке
на
отрезке
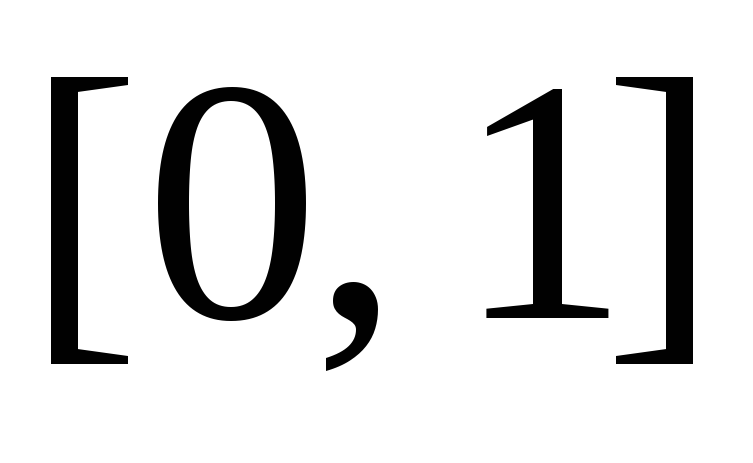 ,
то
,
то
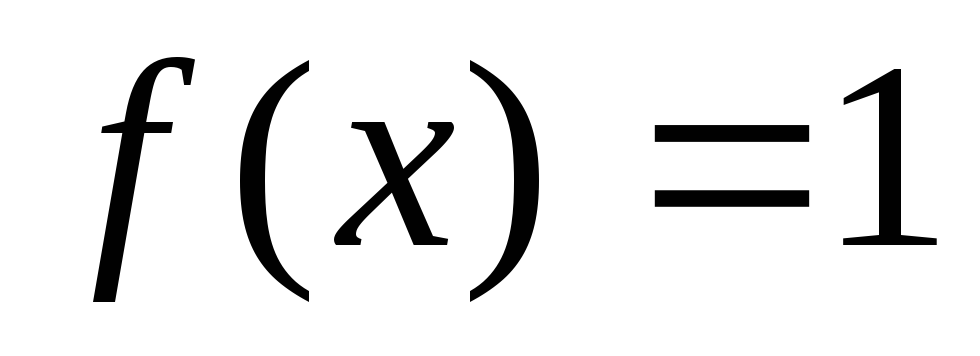 почти всюду.
почти всюду. -
Почему не может существовать измеримой на
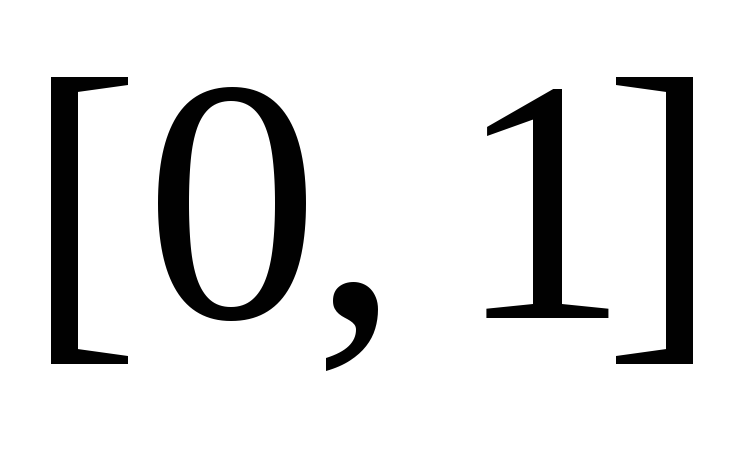 и ограниченной функции, удовлетворяющей
условию
и ограниченной функции, удовлетворяющей
условию
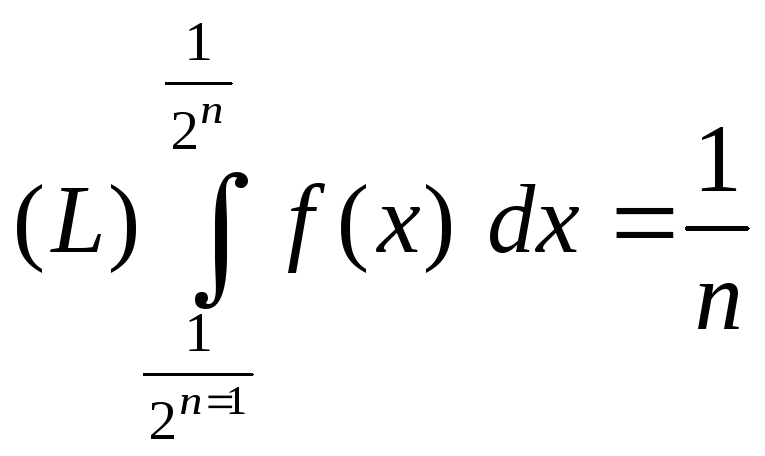 ?
? -
Пусть
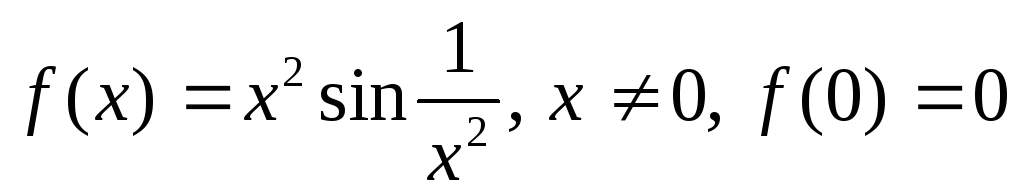 .
Покажите, что производная
.
Покажите, что производная
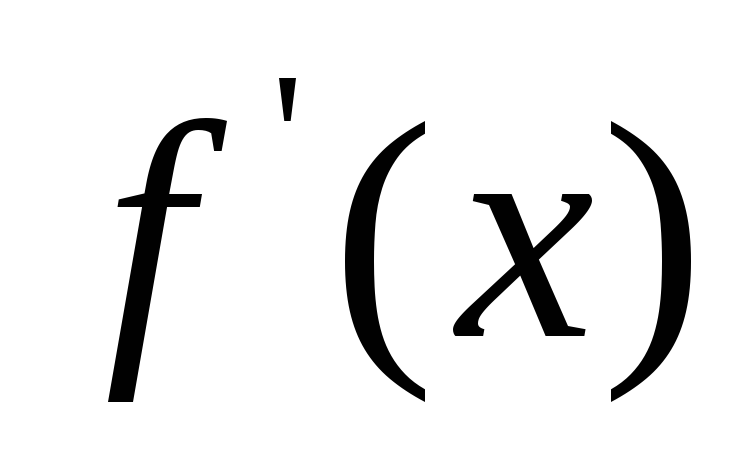 не интегрируема по Риману на
не интегрируема по Риману на
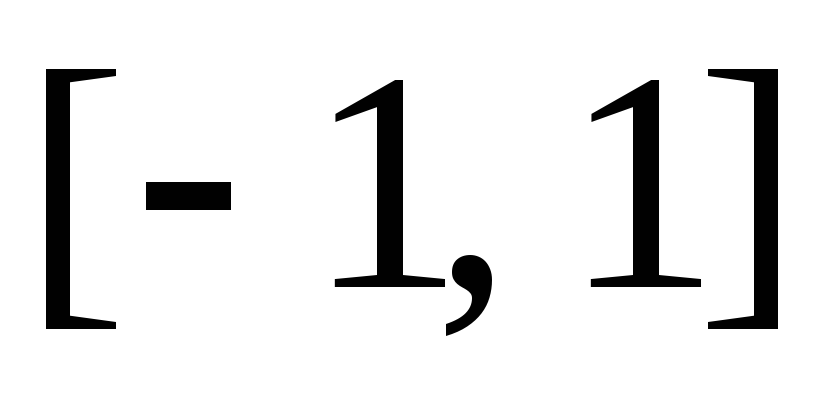 .
.
