
Давыд Цуриков. Диссертация. 2015 г
..pdf31
деле высоких барьеров были исследованы резонансы, возникающие за счёт рассогласования волновых функций внутри и снаружи барьера. Было показано, что эти резонансы имеют качественно другой тип поведения в сравнении с резонансными туннельными пиками.
Дальнейшее развитие применительно к рассеянию в двух измерениях на финитном потенциале формализм R-матрицы получил в работе [28]. Это позволило сформулировать единый метод расчёта S-матрицы для двумерных планарных систем и нанопроволок с цилиндрической симметрией. Предложенный формализм использовался на примерах квантовой точки в двумерном электронном газе и конической квантовой точки, встроенной в цилиндрическую нанопроволоку. Обнаружено, что учёт закрытых каналов для притягивающего потенциала (потенциальной ямы) приводит к появлению характерных углублений на графике коэффициента прохождения как функции энергии электрона.
Также в работе [28] была затронута резонансная теория в терминах R-матрицы применительно к рассмотренным структурам. Учитывая используемое выражение для S- матрицы, было записано уравнение на её сингулярности (полюсы):
det[R(E)iK (E) +1] = 0 |
(64) |
Вещественные решения уравнения (64) интерпретируются как энергии связанных состояний, комплексные – как резонансные энергии.
Объединение S-матриц узлов
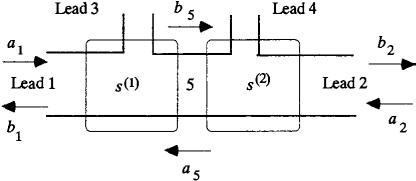
Любую квантовую сеть можно рассматривать, как один узел со сложной структурой, и применить для вычисления её S-матрицы один из рассмотренных выше методов. В этом случае для прямого численного расчёта потребуется провести триангуляцию всей области сети, что увеличит время вычислений. Поэтому может оказаться удобнее сначала найти S- матрицы образующих сеть узлов, а далее на основе их объединения – S-матрицу сети [25, 35]. Данный подход становится особенно эффективным, когда сеть содержит одинаковые узлы. Проиллюстрируем его на примере сети, изображённой на рисунке 5 [25].
Объединённая S-матрица сети s (рис. 5) запишется как объединение S-матриц образующих её узлов s(1) и s(2) :
s = s(1) s(2) |
(65) |
Правило объединения, обозначенное символом , определяется следующим образом. Запишем S-матрицы узлов сети в виде
b |
|
(1) |
a |
|
r(1) |
t′(1) |
a |
|
a |
|
(2) |
b |
|
r(2) |
t′(2) |
b |
|
|
|||
13 |
= s |
|
13 |
|
= t(1) |
|
13 |
, |
5 |
= s |
a |
5 |
|
= t(2) |
|
a |
5 |
|
(66) |
||
b |
|
a |
|
r′(1) |
a |
b |
|
24 |
|
r′(2) |
24 |
|
|||||||||
5 |
|
|
|
5 |
|
|
|
5 |
|
24 |
|
|
|
|
|
|
|
|
|
||
32
где {a13} – вектор-столбец амплитуд падающих волн во всех каналах в проводниках (рука-
вах) ‘1’ и ‘3’, {b13} – вектор-столбец амплитуд рассеянных волн во всех каналах в провод-
никах ‘1’ и ‘3’ и т. д. Матрицы [r] и [r′] описывают амплитуды отражения, матрицы [t] и [t′] описывают амплитуды прохождения; верхние индексы 1 и 2 относятся к двум узлам соответственно. Заметим, что в проводнике ‘5’ {a5} – амплитуды падающих волн для пер-
вого узла и амплитуды рассеянных волн для второго узла. Исключая {a5} и {b5} из систе-
мы (66), получим правило объединения S-матриц, обозначенное в (65) символом :
|
b |
|
a |
|
r t′ a |
|
||
|
13 |
|
= s 13 |
|
= |
13 |
|
|
|
b24 |
a24 |
t r′ a24 |
|||||
r = r(1) +t′(1)r(2)[I −r′(1)r(2) ]−1t(1) , |
|
t′ = t′(1)[I −r(2)r′(1) ]−1t′(2) |
||||||
t = t(2)[I −r′(1)r(2) ]−1t(1) , |
|
|
r′ = r′(2) +t(2)[I −r′(1)r(2) ]−1 r′(2)t′(2) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(67)
(68)
Рис. 5. Пример актуальной сети для объединения S-матриц её узлов s(1) и s(2) .
В записанном выше правиле объединения отсутствует длина рукава ‘5’, соединяющего узлы 1 и 2. Это связано с тем, что границы узлов можно выбрать произвольным образом в пределах рукавов. В результате элементы их S-матриц приобретут только фазовые множители, а транспортные свойства сети останутся прежними. Поэтому в литературе [25, 35], как правило, границы объединяемых узлов формально совмещают друг с другом, что исключает из рассмотрения длины рукавов.
Резюме
Таким образом, для расчёта S-матрицы квантовой сети существует несколько методов. Универсальными и гибкими являются граничные условия рассеяния, обеспечивающие сшивание волновой функции в узле с волновыми функциями в рукавах. Однако их «нестандартный» вид и привязка к конкретной задаче затрудняет их применение во многих вычислительных пакетах. От этого недостатка свободен метод Dirichlet-to-Neumann и
33
Neumann-to-Dirichlet отображений (метод R-матрицы). Будучи основанным на решении граничных задач Дирихле и Неймана, он является более удобным в применении. Тем не менее, он требует вовлечения дополнительных математических соображений для решения исходной задачи рассеяния, что лишает его наглядности. Для расчёта S-матрицы системы узлов используется правило объединения их S-матриц. Распространённый в литературе приём формального совмещения границ узлов упрощает конечный результат, но затрудняет исследование транспортных свойств квантовой сети в зависимости от длин рукавов.
В рассмотренных в разделе 2.1 работах затронут тот или иной аспект расчёта транспортных свойств квантовой сети. Помимо специфических особенностей каждого метода, в разных источниках присутствуют оригинальные системы обозначений. Всё это усложняет реализацию программы на ЭВМ. Схема расчётов, основанная на объединении адаптированных методов в эффективной системе обозначений, позволит упростить реализацию вычислений транспортных свойств квантовой сети.
2.2. Рассеяние электрона в квантовой сети
Изложение объёдинённой схемы расчёта квантового электронного транспорта в низкоразмерных полупроводниковых структурах начнём с постановки задачи. Для этого проведём последовательную формализацию, вводя необходимые соглашения и обозначения.
2.2.1. Соглашения и обозначения
Соглашения
Для упрощения изложения введём следующие соглашения.
1. Индексы и диапазоны. Диапазоны значений верхних и нижних индексов в перечис-
лениях и суммах задаются на соответствующих уровнях, например: {dnl }ln AB , ∑ln AB dnl . Не-
явно заданный диапазон значений индекса определяется его расположением относительно литеры и её семантикой. По умолчанию, любое перечисление в этой работе упорядочен-
ное – кортеж (tuple) [37, с. 33].
2. Векторы и матрицы. Перечисление по одному индексу (например, d ={d l }l ) явля-
ется вектором-столбцом, по двум индексам на одном уровне (например, D ={Dkl }kl ) –
матрицей: первый индекс – номер строки, второй – номер столбца. Объекты с индексамикортежами вне квадратных скобок являются перечислениями по всем элементам кортежа. Например, d A ={d k }k A – вектор, DAB ={Dkl }k A,l B – матрица,
34
A:={1,2}, B:={3,4,5} |
DAB = D{1,2}{3,4,5} = |
D13 |
D14 |
D15 |
(69) |
D23 |
D24 |
D25 |
Также выполняются правила: d = , DA = = D B . Пустые строки и столбцы у матриц исключаются. Нулевые матрицы обозначаются символом O , единичные – символом I .
3. Двухуровневые кортежи в индексах. Двухуровневые кортежи – кортежи вида {k |
}k . |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
m |
Пример работы с ними: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 2 |
4 |
6 |
8 |
|
|
DAB = D |
AB |
0 2 |
4 |
6 |
8 |
D1504 |
D1706 |
D1908 |
|
|
|
A:={1 ,3 }, |
B:={5 |
,7 |
,9 |
} |
|
|
= D{1 ,3 |
}{5 |
,7 |
,9 |
} = D24 |
D26 |
D28 |
|
(70) |
||
|
|
|
|
|
|
|
|
|
|
|
|
35 |
37 |
39 |
|
|
|
4. Немой символ . Для сокращения определений и утверждений используется немой символ . В перечислениях он заменяется указанными для него значениями. Например,
{ f ( ) = | = a,b,c,d,e} |
{ f (a) = a, f (b) = b, f (c) = c, f (d) = d, f (e) = e} |
(71) |
5. Дифференцирование. ∂ |
– оператор частного дифференцирования, где – |
наиме- |
нование переменной (именованное дифференцирование) либо номер аргумента соответствующей функции (нумерованное дифференцирование). Сокращение:
f f := ∂1 f |
(72) |
6.Нотация Айверсона [6, с. 42]. Скобки с утверждением равны 1, если оно истинно, и равны 0, если оно ложно.
7.Черта над символом. Значение черты над символом зависит от его семантики:
число – комплексно сопряжённое число функция – функция с комплексно сопряжёнными значениями оператор – эрмитово сопряжённый оператор область – объединение области с её границей кортеж – дополнение к кортежу
8. Порядок действий. Индексы при символе берутся в последнюю очередь при этом сверху вниз и слева направо: Acdab := (Aab )cd ={[(Aa )b ]c}d . Обратный порядок действий зада-
ёт правило редукции индексов. Аргументы в скобках при функциях также берутся в последнюю очередь, при их частичной редукции ставится троеточие: f (x,...) .
9. Значения редуцированных аргументов. В случаях, когда необходимо указать, к какому множеству принадлежат редуцированные аргументы, используются слова «in» и «on» (обычно для границ областей). Например,

35
[− +υ] f = ε f |
in Ω |
|
[− +υ(r)] f (r) = ε f (r), r Ω |
(73) |
||
|
|
|
|
r ∂Ω |
||
f |
= 0 |
on ∂Ω |
|
f (r )= 0, |
|
|
10. Символика «бра-кет». Семантика объектов в символике «бра-кет» определяется объектами в скобках. В частности, скалярное произведение для функций дискретного и непрерывного аргумента имеет вид
a b |
= ∑n |
[n D(a) ∩D(b)]anbn |
(74) |
|
f g |
= ∫dx[x D( f ) ∩D(g)] f (x)g(x) |
|||
|
||||
где D( ) – область определения функции .
Обозначения
Расширим введённый для квантовой сети в разделе 2.1 понятийный аппарат. Внутренний узел – элемент сети, в котором носитель заряда рассеивается, внешний узел – источник либо приёмник носителей заряда, рукав – элемент сети, в котором носитель заряда не рассеивается, внутренний рукав соединяет два внутренних узла, внешний рукав соединяет внутренний узел с внешним узлом.
Для однозначной идентификации элементов сети пронумеруем её рукава. Во всех обозначениях верхний индекс – номер рукава, нижний индекс – номер канала, верхний индекс в квадратных скобках – идентификатор узла, содержимое скобок – кортеж номеров примыкающих к узлу рукавов (рис. 6).
Ω2
|
|
|
Γ[A]2 |
|
|
|
|
Ω[A] |
|
|
|
Ω1 Γ[A]1 |
Γ[A]k |
Ωk |
|
|
Рис. 6. Участок квантовой сети. |
||
На рисунке 6 |
Ω[A] – |
узел ( A N ), {Ωk }k A – |
рукава, примыкающие к узлу Ω[A] , |
|
Γ[A]k := ∂Ω[A] ∩∂Ωk |
– граница узла Ω[A] с рукавом Ωk , Γ[A] := k AΓ[A]k – граница узла Ω[A] |
|||
с примыкающими рукавами. Также в работе используются обозначения: I – кортеж номе- |
||||
ров внутренних рукавов, |
E – кортеж номеров внешних рукавов, N – кортеж идентифи- |
|||
каторов внутренних узлов, содержащий информацию обо всех соединениях узлов.
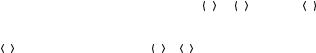
36
Особенности идентификаторов
Наряду с «рукавными» идентификаторами узлов применимы «узловые». «Узловой» идентификатор помещается в угловые скобки и может быть цифрой, буквой или словом. Он имеет ряд преимуществ.
•Краткость. При наличии большого числа рукавов, примыкающих к узлу, его «рукавный» идентификатор становится громоздким. «Узловой» можно записать компактнее.
•Конкретность. «Узловой» идентификатор удобен при конкретизации структуры сети по типу внутренних узлов:
{Ω[K] = Ω A | a A = a[K],b A = b[K],...}K A |
(75) |
где Ω A – узел типа «A», a A ,b A ,... – параметры узла типа «A», {a[K],b[K],...}K A – значе-
ния параметров узлов типа «A» в сети, A – кортеж идентификаторов узлов типа «A». Несмотря на достоинства «узловых» идентификаторов, основными в данной работе
являются «рукавные». Это связано с их существенными для изложения свойствами.
•Наглядность. «Рукавный» идентификатор однозначно локализует узел в сети, содержит информацию о блочной структуре его S-матрицы. Связи между узлами можно выявить по их «рукавным» идентификаторам.
•Универсальность. Любой участок сети с произвольной внутренней узловой структурой имеет естественный «рукавный» идентификатор.
2.2.2. Постановка задачи
Носитель заряда в сети
Рассмотрим трёхмерную квантовую сеть. Полученные для неё результаты легко конкретизируются для одномерных и двумерных сетей. Не умаляя общности подхода, для простоты изложения будем рассматривать изотропный полупроводник. Движение носителя заряда описывается уравнением Шрёдингера
|
(− |
2 |
+V )ϕ = Eϕ |
(76) |
|
2m |
|||
где – постоянная Планка, m – |
эффективная масса носителя заряда, |
= ∂12 +∂22 +∂32 – |
||
оператор Лапласа, V – потенциал, |
E – |
энергия носителя заряда. Запишем его в безраз- |
||
мерном виде |
|
|
|
|
|
(− |
+υ)Ψ = εΨ |
(77) |
|
37
υ(r ):= 2m −2 L2V (Lr ), ε := 2m −2L2E, Ψ(r ):= L3/2ϕ(Lr ) |
(78) |
где L – характерная длина (можно выбрать любой из соображений удобства в конкретной задаче). Тогда движение носителя заряда описывается граничными задачами для безразмерных уравнений Шрёдингера в рукавах
[−k |
+υ |
|
]Ψ |
|
= εΨ |
|
|
in Ω |
k |
|
k , k I E |
(79) |
||||||
|
|
|
|
k |
|
|
k |
|
k |
|
k |
|
|
|
|
|
||
Ψ = 0 |
|
|
|
|
|
|
|
on ∂Ω \ Γ |
|
|
|
|
||||||
и внутренних узлах сети |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[A] |
]Ψ |
[A] |
= εΨ |
[A] |
|
[A] |
|
|
|
|
||||
[− +υ |
|
|
|
|
in Ω |
|
|
[A] , |
A N |
(80) |
||||||||
|
[A] |
= 0 |
|
|
|
|
|
|
|
|
|
[A] |
\ Γ |
|||||
Ψ |
|
|
|
|
|
|
|
|
on ∂Ω |
|
|
|
||||||
где Γk – граница рукава ницах внутренних узлов
Ωk с прилегающими к нему узлами, и условий сшивания на гра-
срукавами.
Ψ[A] = Ψk |
|
|
|
|
|
on Γ[A]k , k A N |
(81) |
∂ Ψ[A] = ∂ Ψk |
|||
|
n |
|
|
n |
|
|
|
Уравнения (79), (80) и условие (81) записаны в глобальной системе координат (ГСК) – системе координат, связанной с сетью. Её расположение задаётся в конкретной задаче из соображений удобства.
Носитель заряда в рукаве
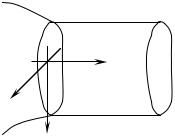
На рисунке 7 изображён произвольный рукав квантовой сети. Здесь [XYZ ][A]k – ло-
кальная система координат (ЛСК) при узле Ω[A] в рукаве Ωk (на границе Γ[A]k ).
Ω[A]
Ωk
X [A]k
Y[A]k
Z[A]k
Рис. 7. Рукав квантовой сети.
Смена систем координат происходит с помощью следующих операторов: W [A]k пере-
водит функции, заданные в ГСК, в функции, заданные в ЛСК [XYZ ][A]k , w[A]k выражает глобальные координаты через локальные. Оператор W [A]k унитарен:

38
W [A]kW |
[A]k = I[A]k =W |
[A]kW [A]k |
(82) |
Так как рукава являются квантовыми проволоками, они имеют простую геометрию:
ω[A]k :={r R3 | w[A]k r Ωk } =α[A]k ×β[A]k |
(83) |
где β[A]k – поперечное сечение рукава Ωk в ЛСК [XYZ ][A]k . Начала всех ЛСК находятся в началах рукавов:
α[A]k = (0,ak ) |
(84) |
где ak – длина рукава Ωk , а границы узла с рукавами имеют вид |
|
γ[A]k :={r R3 | w[A]k r Γk } ={0}×β[A]k |
(85) |
Движение носителя заряда в области Ωk в ГСК описывается уравнением (79). Чтобы разделить переменные в задаче (79), перейдем из ГСК в ЛСК:
ψ[A]k (r ):=W [A]k Ψk (r )= Ψk (w[A]k r )
(86)
u[A]k (r ):=W [A]kυk (r )=υk (w[A]k r )
и будем полагать, что потенциал υk не изменялся вдоль рукава. Так как при этом рукава имеют простую геометрию (83), получим следующий аналог задачи (79) в ЛСК:
|
|
[A]k |
|
[A]k |
(x, y, z)= εψ |
[A]k |
(x, y, z), |
{x, y, z} α |
[A]k |
×β |
[A]k |
− +u |
|
(y, z) ψ |
|
|
|
||||||
|
|
|
|
|
|
|
|
{x, y, z} α[A]k ×∂β[A]k |
|||
ψ[A]k (x, y, z)= 0, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Ищем решение уравнения (87) в виде
ψ[A]k (x, y, z)=: g[A]k (x)h[A]k (y, z)
Подставляя (88) в (87) получим
[−∂[A]ky −∂z +u |
|
]hm |
= λm |
hm |
|
in β |
|
[A]k |
||
|
2 2 |
|
[A]k |
[A]k |
[A]k [A]k |
|
[A]k |
|||
hm |
= 0 |
|
|
|
|
|
|
on ∂β |
|
|
|
−∂2 g |
[A]k |
= (ε −λ[A]k )g[A]k |
in α[A]k |
|
|
||||
|
x |
m |
|
m |
|
m |
|
|
|
|
Отсюда следует
ψ[A]k (x, y, z) = ∑m cm[A] k exp(−iκm[A]k x)hm[A]k (y, z)+
+∑m cm[A] k exp(+iκm[A]k x)hm[A]k (y, z)
κm[A]k := ε −λm[A]k
(87)
(88)
(89)
(90)
(91)
(92)

39
где c[A] k – амплитуды волн, падающих на узел Ω[A] из рукава Ωk в [XYZ ][A]k , c[A] k – ам-
плитуды волн, рассеянных узлом Ω[A] в рукав Ωk в [XYZ ][A]k ( c[A] k и c[A] k – волновые
амплитуды), λ[A]k – энергии каналов в рукаве Ωk . Всюду ниже полагаем, что функции h[A] являются ортонормированными:
Imn[A]kk = hm[A]k hn[A]k , |
I[A]kk = ∑n |
hn[A]k hn[A]k |
|
(93) |
||
Выражение (91) также удобно записывать в терминах оператора K[A] |
в двух эквивалент- |
|||||
ных представлениях: |
|
|
|
|
|
|
ψ[A]k (x, y, z) = ∑m exp(−iK[A] x)c[A] |
mk hm[A]k (y, z)+ |
|
(94) |
|||
+ ∑m exp(+iK[A] x)c[A] |
mk hm[A]k (y, z) |
|
||||
|
|
|||||
Kmn[A]kl := Imn[A]klκm[A]k |
|
|
|
(95) |
||
ψ[A]k (x, y, z) = ∑m exp(−iK[A] x)h[A] (y, z) |
k |
|
|
|||
m cm[A] k + |
|
(96) |
||||
+ ∑m exp(+iK[A] x)h[A] (y, z) |
k |
|
||||
|
|
|||||
m cm[A] k |
|
|
||||
K[A]kl := I[A]kl ∑n hn[A]k κn[A]k |
hn[A]k |
|
|
(97) |
||
Сгруппируем падающие и рассеянные волны в (91) |
|
|
|
|
||
ψ[A]k =ψ[A] k +ψ[A] k |
|
|
|
(98) |
||
ψ[A] k := ∑mψm[A] k , |
ψ[A] k := ∑mψm[A] k |
|
(99) |
|||
ψm[A] k (x, y, z):= exp(−iK[A] x)c[A] |
k |
|
|
|
k |
|
m hm[A]k (y, z)= exp(−iK[A] x)h[A] (y, z) m cm[A] k |
(100) |
|||||
ψm[A] k (x, y, z):= exp(+iK[A] x)c[A] |
k |
|
|
|
k |
|
|
|
|
|
|||
m hm[A]k (y, z)= exp(+iK[A] x)h[A] (y, z) m cm[A] k |
|
|||||
Задача рассеяния
Можно сформулировать две задачи рассеяния:
•входная задача рассеяния – поиск рассеянных волн по известным падающим;
•выходная задача рассеяния – поиск падающих волн по известным рассеянным. Амплитуды падающих и рассеянных волн с учётом всех каналов связывает расширенная
матрица рассеяния (extended scattering matrix) S[A] узла Ω[A] [35, с. 155]:
cm[A] k = ∑ln Smn[A]klcn[A] l |
(101) |
40
cm[A] k = ∑ln[(S[A] )−1]mnkl cn[A] l |
(102) |
всюду в разделах 2.2, 2.3 и 3.2–3.5 кратко: S-матрица (см. также замечание к терминологии в приложении H). Для интерпретации выражений здесь и ниже удобны мнемонические правила:
c[A] «откуда» , |
c[A] «куда» , |
S[A]«куда»«откуда» |
(103) |
«откуда» |
«куда» |
«куда»«откуда» |
|
Таким образом, решить входную и выходную задачу рассеяния можно, найдя матрицы и (S[A] )−1 соответственно. Заметим, что здесь понятие узла условно: в зависимости от
идентификатора A это может быть любой участок сети, а также вся сеть при A = E.
2.2.3.S-матрица узла квантовой сети
Вэтом подразделе для краткости редуцируем идентификатор узла A . Его всегда можно восстановить, поместив на первом месте в верхнем индексе литеры.
Граничные условия рассеяния
Получим прямой метод расчёта S-матрицы узла квантовой сети (рис. 6). Для этого обобщим граничные условия рассеяния [29–31], повысив их наглядность. Дополним задачу (80) условиями на границах с рукавами. Перепишем условия сшивания (81) в ЛСК с учётом (85):
W Ψ =ψ |
on γ |
(104) |
|
||
∂1W Ψ = ∂1ψ |
|
|
Здесь индекс рукава редуцирован, и все выражения с векторными и матричными объектами (W , ψ , ω , γ , K и т.д.) являются векторными (см. соглашения подраздела 2.2.1). Вос-
пользовавшись формой записи (98), для производной от функции в рукавах получим
∂1ψ = −iKψ |
+iKψ in ω |
(105) |
|
Из соотношений (94), (104) и (105) следует |
|
|
|
|
|
|
|
W Ψ =ψ +ψ |
|
on γ |
(106) |
|
+iKψ |
||
∂ W Ψ = −iKψ |
|
|
|
1 |
|
|
|
Исключая из выражений (106) функции ψ , имеем входные граничные условия рассеяния
(входные ГУР):
[K +i∂1]W Ψ = 2Kψ on γ |
(107) |
