
Давыд Цуриков. Диссертация. 2015 г
..pdf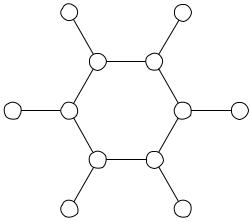
121
2 9 3
1 |
8 |
10 |
4 |
|
|
||
|
7 |
11 |
|
6 |
12 |
5 |
|
Рис. 27. Схема гексагональной квантовой сети. Сплошные линии – внутренние узлы и рукава, пунктирные линии – внешние узлы и рукава.
Будем полагать, что
{ak = 0}k I E |
(348) |
Это не умаляет общности задачи, так как границы узлов с рукавами условны. В любой сети их можно провести так, что будет выполнено равенство (348). При этом узлы модифицируются, а рассеивающие свойства сети останутся прежними.
Одноканальное приближение
Движение электрона в гексагональной квантовой сети (рис. 27) описывает её расши-
ренная матрица рассеяния S[E] . S-матрицу сети можно найти на основе S-матриц её узлов посредством сетевой формулы (167). Операция объединения (164) определяется согласно формуле объединения (160), которая в случае (348) имеет вид
|
[J,K]JJ |
|
JL |
|
[J,K]JK |
|
JK |
|
|
|||||
S[J,L] = S |
|
O |
|
|
+ S |
|
|
|
O |
|
|
× |
|
|
|
OLJ S[K,L]LL OLK S[K,L]LK |
|
(349) |
|||||||||||
|
|
[J,K]KK |
|
|
KK |
−1 |
|
[J,K]KJ |
|
KL |
||||
|
|
|
|
|
||||||||||
× −S |
I KK |
|
I |
|
|
|
S |
|
|
O |
|
|
|
|
|
|
−S[K,L]KK |
|
OKJ |
|
S[K,L]KL |
||||||||
Расширенные матрицы рассеяния в формуле (167) являются бесконечными в силу бесконечного числа каналов в рукавах. В численных расчётах конкретных физических систем учитывается их конечное число. При расчёте S[E] учтём только первый открытый канал: {κmk }km ={κ1k }k , {Im(κ1k ) = 0}k . Тогда (167) примет вид:
A N |
(350) |
|
S[E] ≈ |
S[A] |
|
11 |
11 |
|

122
Выражение (350) – одноканальное приближение для S-матрицы квантовой сети. В этом случае, согласно выражению для C-матрицы (198) и свойству (347), S11 = C11 . Поскольку первый канал является открытым, C11 унитарна (200). Следовательно, S11 унитарна также:
S11 |
|
11 = I11 = |
|
11S11 |
(351) |
S |
S |
и квадраты модулей её элементов имеют вероятностную интерпретацию. Здесь выражение (351) верно для матриц с любым идентификатором узла.
Для гексагональной сети (рис. 27) имеем
|
|
|
|
{S11[A] = S11Y }A N |
|
(352) |
где S Y |
– матрица |
S |
++ |
симметричного Y-узла. Поэтому для расчёта |
S[E] |
посредством |
11 |
|
|
|
11 |
|
|
(350) следует найти |
S |
Y . |
|
|
|
|
|
|
11 |
|
|
|
|
S-матрица симметричного Y-узла
Вид S11Y как функции энергии определяется геометрией узла и электростатическим потенциалом в нём. Чтобы выявить характерные особенности транспортных свойств сети во всевозможных случаях, проведём параметризацию S-матрицы симметричного Y-узла.
 имеет следующую структуру:
имеет следующую структуру:
|
μ1 |
μ2 |
μ2 |
|
|
||||
S Y |
= |
μ |
2 |
μ |
μ |
2 |
|
(353) |
|
11 |
|
|
|
1 |
|
|
|
||
|
|
μ |
2 |
μ |
2 |
μ |
|
|
|
|
|
|
|
|
1 |
|
|
||
Из (351) и (353) следует
μ |
μ |
+ 2μ |
μ |
|
=1 |
|
|
(354) |
||
1 1 |
2 |
|
2 |
|
|
|
||||
μ1 |
μ |
2 + μ2 |
μ1 + μ2 |
μ |
2 = 0 |
|
||||
Полагая, что μ1,2 =: ρ1,2 exp(iϕ1,2 ) , из (354) получим
|
2 |
2 |
=1 |
(355) |
|
ρ1 |
+ 2ρ2 |
||
2ρ1 cos(ϕ1 −ϕ2 ) + ρ2 = 0 |
|
|||
Введём обозначение:
η := −cos(ϕ1 −ϕ2 ) |
(356) |
123
Так как модули комплексных чисел неотрицательны: ρ1,2 ≥ 0 , из второго равенства систе-
мы (355) и (356) следует
|
|
|
|
|
|
|
0 ≤η ≤1 |
|
|
|
(357) |
||||
С учётом (356) систему (355) запишем в виде |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
2 |
=1 |
|
|
|
|
|
|
|
|
|
|
|
ρ1 |
+ 2ρ2 |
|
|
|
(358) |
|||
|
|
|
|
|
|
|
|
2 ρ |
2 = |
ρ2 |
|
|
|
||
|
|
|
|
|
|
4η |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
Отсюда имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ = (1+8η2 )−1/2 |
, |
ρ |
2 |
= 2η(1+8η2 )−1/2 |
|
|
(359) |
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Вводя обозначение θ :=ϕ1 , из (356) получим |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
ϕ2 =θ −arccos(−η) |
|
|
|
(360) |
|||||
Таким образом, согласно (359) и (360) имеем параметризацию для S Y |
(353): |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
2 |
|
−1/2 |
exp(iθ) |
|
|
|
|
|
|
|
|
|
μ1 = (1+8η |
) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
, 0 |
≤η ≤1, 0 |
≤θ ≤ 2π |
(361) |
||||||
|
|
= 2η(1+8η2 )−1/2 exp(i[θ |
|
|
|
|
|||||||||
μ |
2 |
−arccos(−η)]) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Численный расчёт
На основе (350), (352), (353) и (361) найдём матрицу коэффициентов рассеяния гексагональной квантовой сети (рис. 27)
P[E] ={| S[E]kl |2 |
}k ,l E |
(362) |
|
11 |
11 |
|
|
Графики её элементов как функций параметра z =ηeiθ изобразим в комплексной плоско-
сти. Область определения каждого из них – замкнутый единичный круг: {z C|| z |≤1} (рис. 28, слева). Каждая точка круга будет иметь оттенок, отвечающий значению коэффициента рассеяния в ней. Соответствие значения оттенку задаёт палитра (рис. 28, справа).
График матрицы коэффициентов рассеяния (362) (рис. 29) имеет симметрию, анало-
гичную симметрии сети (рис. 27). В первой строке уникальны элементы P11[E]11 , P11[E]12 ,
P11[E]13 , P11[E]14 , при этом P11[E]15 = P11[E]13 , P11[E]16 = P11[E]12 . Каждая строка (столбец) связана с со-
седними циклической перестановкой элементов. На рисунке видно, что коэффициенты рассеяния π -периодичны по параметру θ , что объясняется спецификой параметризации. Графики диагональных элементов говорят о преобладании отражения (тёмные участки) и возможности существенного прохождения (светлые участки). Наблюдается пониженная

124
вероятность прохождения в чётные рукава при чётном входном рукаве, а также в нечётные при нечётном входном.
|
1 |
Im(z) |
|
|
1.0 |
|
|
||||
|
z = ηeiθ |
||||
|
|
||||
|
|
|z| ≤ 1 |
1 |
|
|
–1 |
0 |
|
0.5 |
||
|
Re(z) |
||||
–1
0.0
Рис. 28. Правило построения графиков коэффициентов рассеяния. Слева – область определения коэффициента, справа – палитра его значений в области.
Рис. 29. График матрицы коэффициентов рассеяния гексагональной квантовой сети в одноканальном приближении.
Каждой реализации симметричного Y-узла соответствует кривая в замкнутом единичном (рис. 28), которая характеризует поведение параметров η и θ как функций ε . Со-
вместив кривую с графиками коэффициентов рассеяния (рис. 29), можно оценить рассеивающие свойства гексагональной сети, состоящей из Y-узлов данного типа.
125
Резюме
В этом приложении рассмотрена задача численного моделирования аллотропных модификаций углерода (графен, фуллерен, нанотрубки) [А5]. Функциональную модель их кристаллической решётки предложено построить на основе задачи рассеяния электрона в гексагональной квантовой сети. В рамках одноканального приближения сформулирована параметризация S-матриц симметричных Y-узлов, образующих сеть. Это позволило отойти от конкретной геометрии узла, потенциала в нём и энергии электрона. Задача сведена к анализу рассеяния в зависимости от одного комплексного параметра, область значений которого – замкнутый единичный круг. В итоге рассчитаны коэффициенты рассеяния гексагональной квантовой сети, состоящей из произвольных одинаковых узлов. Выявлено преобладание отражения электрона от сети, а также возможность существенного прохождения. Установлено, что для всех сетей данного типа прохождение электрона имеет минимальную вероятность для выходных рукавов, находящихся через один от входного.
Приложение F. Адаптированный формализм Ландауэра–Бюттикера
В подразделе 2.3.2 формализм Ландауэра–Бюттикера был адаптирован к используемой системе обозначений (подраздел 2.2.1). В этом приложении приведено математическое сопровождение к нему, которое дополняет изложенный выше материал, а также демонстрирует эффективность оригинальной системы обозначений.
Выражение для токов
Для повышения наглядности математических выкладок при манипуляциях с матрицей вероятностей рассеяния (212) будем записывать в явном виде скобки Айверсона, присутствующие в её определении: Pmnkl (E )=[Ekm < E]Pmnkl (E)[E > El n ] . Тогда согласно (213)– (217) получим
J k = ∑m ∫−∞+∞ dE{− |
e |
f k (E)[Ek m < E] +[Ek m < E]∑ln Pmnkl (E) |
e |
f l (E)[El n < E]}= |
|
|||||||||||||||||||
π |
π |
|
||||||||||||||||||||||
= |
e |
|
|
+∞ dE[Ek |
< E] |
{ |
− f k (E)+ |
|
l |
[El |
< E]Pkl |
(E) f l (E) |
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
∑n |
|
|
||||||||||||||||||||
|
π ∑m ∫−∞ |
m |
|
|
|
|
n |
mn |
|
|
} |
|
|
|
||||||||||
{...}= − f |
|
(E)∑n |
[E n < E |
]Imn + ∑n [E n < E]Pmn (E) f |
|
(E)+ |
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
k |
|
|
|
|
k |
|
|
|
kk |
|
k |
|
kk |
|
k |
|
|
|
|
|
|
|
|
l≠k |
|
l |
|
|
kl |
|
|
l |
(E)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+∑n |
[E n < E |
]Pmn (E) f |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
l≠k |
|
l |
|
|
kl |
|
f |
l |
(E)− f |
k |
(E)∑n |
k |
|
|
kk kk |
|
|
|
||||
|
= ∑n [E n < E |
]Pmn (E) |
|
|
[E n < E] Imn − Pmn |
(E) |
|
|
||||||||||||||||

126
|
|
|
|
|
J k = |
e |
∑m ∫−∞+∞ dE[Ek m < E]{...} |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
π |
|
|
|
|
|
|
|
(363) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
l≠k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
kl |
|
|
l |
|
|
|
k |
k |
kk |
kk |
|
||
|
|
|
|
|
|
{...}= ∑n |
|
|
< |
|
E |
|
|
|
f |
(E)− f |
||||||||||||||
|
|
|
|
|
|
[E n |
|
]Pmn (E) |
|
|
(E)∑n [E n |
< E] Imn − Pmn (E) |
||||||||||||||||||
Упростим выражение (363). Для этого применим свойство унитарности (200): |
|
|||||||||||||||||||||||||||||
[mk ,qp O]∑ln [ln O]Cmnkl C |
nqlp =[mk ,qp O]Imqkp ; |
|
|
|
|
mk =qp |
|
|
|
|
|
|||||||||||||||||||
[mk O]∑ln [ln O]Cmnkl C |
nmlk |
=[mk O]Immkk |
; (212) |
|
|
|
|
|
|
|||||||||||||||||||||
[mk O]Immkk =[mk O]∑ln [ln O]Pmnkl =[mk O]∑ln ([ln =nk ]+[ln ≠nk ])[ln O]Pmnkl = |
|
|
||||||||||||||||||||||||||||
=[mk O]∑n [nk O]Pmnkk +[mk O]∑ln≠k [ln O]Pmnkl |
|
|
|
|
|
|||||||||||||||||||||||||
[mk O]∑ln≠k [ln O]Pmnkl =[mk O]{Immkk −∑n [nk O]Pmnkk }= |
|
|
|
|||||||||||||||||||||||||||
=[mk O]{∑n [nk O]Imnkk −∑n [nk O]Pmnkk } |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
[mk O]∑ln≠k [ln O]Pmnkl |
=[mk O]∑n [nk O]{Imnkk − Pmnkk } |
|
(364) |
||||||||||||||||||
Перепишем свойство (364) в эквивалентном виде: |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
[Ek m < E]∑ln≠k [El n |
< E]Pmnkl (E)=[Ek m |
|
< E]∑n [Ek n < E]{Imnkk − Pmnkk (E)} |
(365) |
||||||||||||||||||||
Тогда из (363) и (365) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
{...}= ∑ln≠k [El n |
< E]Pmnkl |
(E) f l (E)− f k (E)∑ln≠k [El n < E]Pmnkl (E) |
|
|
|
|||||||||||||||||||||||||
{ } |
|
|
∑n |
n |
|
mn |
( |
|
){ |
|
|
( |
|
|
) |
|
( |
|
|
)} |
|
|
|
|
|
|
|
|||
... |
|
= |
|
l≠k [El |
< E]Pkl |
|
E |
|
f l |
|
E |
|
− f k |
|
E |
|
; (363) |
|
|
|
|
|||||||||
J k |
= |
e |
∑lmn ∫−∞+∞ dE[Ekm < E][El n < E]Pmnkl (E){f l (E)− f k (E)}. |
Исключая |
избыточные со- |
|||||||||||||||||||||||||
π |
||||||||||||||||||||||||||||||
гласно определению (212) скобки Айверсона, имеем |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
J k = |
e |
∑lmn ∫−∞+∞ dEPmnkl (E){f l (E)− f k (E)} |
|
(366) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
π |
|
||||||||||||||||||
где {Pkl |
}l≠k |
– матричные коэффициенты прохождения в k-й рукав. Формула (366) в случае |
||||||||||||||||||||||||||||
|
|
|
|
mn |
mn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
двухконтактного проводника совпадает с результатом (49) работы [26]. |
|
|
||||||||||||||||||||||||||||
|
|
Отметим, что выше в суммах и наборах с индексом l ≠ k |
свёртка только по первому |
|||||||||||||||||||||||||||
символу: l |
– немой символ, |
k |
– свободный. Например, |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∑l≠k {...}= ∑l [l ≠ k]{...}≠ ∑kl [l ≠ k]{...} |
|
|
||||||||||||||||
127
Электронные и дырочные токи
Выясним, как модифицируется формула для токов (366), когда необходимо использо-
вать систему отсчёта по энергии с учётом уровней зоны проводимости EC и валентной зоны EV . Поскольку в формуле (366) от выбора системы отсчёта зависит только уровень Ферми, в ней следует выполнить замены
Ek |
Ek |
− E |
(367) |
F |
F |
C |
|
Ek |
E − Ek |
(368) |
|
F |
V |
F |
|
для электронов и дырок соответственно. Это приведёт к модификации функций распределения (207)
f k (E)= |
|
1 |
|
|
(369) |
|
exp[(E − Ek |
+ E |
) / (k T k )] +1 |
||||
|
|
|||||
|
F |
C |
0 |
|
|
|
f k (E)= |
|
1 |
|
|
(370) |
|
exp[(E − E |
+ Ek ) / (k T k )] +1 |
|||||
|
|
|||||
|
V |
F |
0 |
|
|
|
для электронов и дырок соответственно. В выражении для тока (366) также следует учесть заряд носителей:
e = −e0 |
(371) |
e = +e0 |
(372) |
для электронов и дырок соответственно, где e0 – элементарный заряд. |
|
Когда в решаемой задаче не учитываются уровни разрешённых зон EC |
и EV , в фор- |
муле для токов (366) актуален только заряд носителей (371) и (372). |
|
Малые напряжения смещения
Пусть уровни Ферми резервуаров близки к уровню Ферми структуры EF
{EFk → EF }k E |
(373) |
Это происходит в случае малых напряжений смещения (223). Допустим, что температуры резервуаров равны (229). Тогда согласно (207) и (229) запишем
f k (E)= f (E, EFk ) |
|
|
|
(374) |
|||
f (E, EF ):= |
|
1 |
|
|
|
(375) |
|
exp[(E − E |
|
|
= |
)] +1 |
|||
|
F |
) / (k T |
|
|
|||
|
|
|
0 |
|
|
|
|

128 |
|
Разложив в (222) f k и f l в ряд как функции уровня Ферми, в точке EF |
с точностью до |
линейных слагаемых, получим |
|
f l (E)− f k (E)→ (EFl − EFk )∂2 f (E, EF ) |
(376) |
Тогда в приближении (373) с учётом (223) и (376) для средней вероятности рассеяния
(222) имеем
Pmnkl → Pmnkl := ∫−∞+∞ dEPmnkl (E)∂2 f (E, EF ) |
(377) |
На основе (374) и (375) выражение для ∂2 f можно записать в виде
∂2 f (E, EF )= |
1 |
|
ch−2 ([EF − E] / [2k0T = ]) |
(378) |
4k T |
= |
|||
|
|
|
|
|
|
0 |
|
|
|
График правой части (378), как функции энергии имеет колоколообразную форму с пиком в точке EF . Это означает, что наибольший вклад в среднюю прозрачность будут вносить уровни {Ek m}km , находящиеся вблизи EF .
С учётом (378) приближение для средней вероятности рассеяния (377) удобно записать в терминах безразмерных величин
Pmnkl = |
1 |
|
∫−∞+∞ dε[λmk |
< ε] |
|
Cmnkl (ε ) |
|
2 [ε > λnl ]ch−2 ([εF −ε] / [2μ= ]) |
(379) |
|
|
|
|
||||||||
4μ |
= |
|||||||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||
Согласно (221), выражение для приближённой проводимости примет вид |
|
|||||||||
|
|
|
|
σ kl := πe2 ∑mn Pmnkl |
(380) |
|||||
В терминах неё с учётом (220) и (380) можно записать выражения для электрических токов при малых напряжениях смещения:
J k = ∑l σ klU lk |
(381) |
Поскольку приближённая проводимость σ не зависит от уровней Ферми резервуаров, зависимость электрических токов от напряжения смещения при его малых значениях становится линейной.
Низкие температуры
Рассмотрим случай низких температур:
maxk {T k } → 0 |
(382) |

129
В приближении (382) функция распределения (207) примет вид
|
|
|
|
|
|
f k (E)→[E < EFk ] |
|
|
|||
С учётом (383) для выражения (218) запишем |
|
|
|
|
|||||||
J k → |
e |
∑lmn ∫−∞+∞ dEPmnkl (E){[E < EFl ] −[E < EFk ]} |
|
|
|
|
|||||
π |
|
|
|
|
|||||||
|
|
|
|
0 |
E < EFl , E < EFk |
|
|
|
|
||
|
|
|
|
|
|
E < El , |
E ≥ Ek |
|
Ek |
< El |
|
[E < EFl |
] −[E < EFk |
+1 |
|
||||||||
] = |
|
F |
F |
|
F |
F |
|||||
|
|
|
|
−1 |
E ≥ EFl , E < EFk |
EFk > EFl |
|
||||
|
|
|
|
|
|
l |
k |
|
|
|
|
|
|
|
|
0 |
E ≥ EF , |
E ≥ EF |
|
|
|
|
|
[E < EFl ] −[E < EFk ] = sgn (EFl − EFk )[min(EFk , EFl ) ≤ E < max(EFk , EFl ]
J k → πe ∑lmn ∫dE[E (EFk , EFl )]Pmnkl (E)
Отметим, что здесь используется соглашение:
(383)
(384)
a,b ∫dx[x (a,b)]{...}= ∫ab dx{...}= −∫ba dx{...}= −∫dx[x (b, a)]{...} |
(385) |
При интегрировании переменная принимает значения согласно «направлению» интервала, к которому принадлежит (здесь интервал – 1D аналог ориентированной кривой, задающей направление интегрирования).
Выражение (384) имеет простую физическую интерпретацию: за электрический ток в k-м рукаве отвечают рукава-каналы, энергии которых {Ek m}km находятся между уровнем Ферми k-го резервуара и уровнями Ферми всех остальных резервуаров.
Приложение G. Особенности численной реализации
В этом приложении приведены краткие сведения об особенностях численной реализации развиваемой в работе объединённой схемы расчёта квантового электронного транспорта в низкоразмерных полупроводниковых структурах.
Объектно-ориентированный подход
В основе численной реализации лежит оригинальный программный код на языке C++, базирующийся на объектно-ориентрованной парадигме. Разработанная иерархия вычислительных классов состоит из трёх уровней, различающихся по степени абстракции решаемой задачи. Классы уровня I служат для расчёта транспортных свойств и оптимизации параметров произвольной квантовой сети. В классах уровня II происходит частичная кон-
130
кретизация сети в соответствии с её типом, определяемым набором типовых узлов. Классы уровня III полностью конкретизируют сеть и выводят финальный результат расчёта.
Такая организация программного кода имеет следующие преимущества:
•гибкость – возможность легко адаптировать код к конкретной задаче;
•универсальность – возможность решать широкий круг задач: от расчёта транспортных свойств параметризованной сети (приложение E) до моделирования наноэлектронных устройств (разделы 3.3–3.5).
Диаграмма классов UML
Описанную трёхуровневую иерархию наследования проиллюстрируем на примере задачи о логическом элементе XOR (раздел 3.5) с помощью диаграммы классов UML (Unified Modeling Language) [70, с. 277] в аспекте реализации на C++ (рис. 30). Диаграмма яв-
ляется упрощённой, так как содержит не все используемые классы, а также только малую часть их атрибутов и операций.
На диаграмме классы изображены прямоугольниками, разбитыми на три блока в соответствии с их элементами: имя, атрибуты, операции. Прямоугольники соединяются линиями. Линия с треугольником на конце указывает на базовый класс для данного [71, с. 373]. Линия с ромбом на конце указывает на класс, агрегирующий данный [71, с. 867]. Записанное курсивом имя класса говорит о том, что класс абстрактный, то есть содержит хотя бы одну абстрактную операцию (виртуальную функцию) [71, с. 385]. Абстрактные операции также выделяются курсивом и конкретизируются в производных классах.
Уровень I. Корневые классы
Класс QuantNet реализует расчёт S-матрицы произвольной квантовой сети в терминах S-матриц её узлов с помощью сетевой формулы (167). Он агрегирует классы JcInNet и BrInNet – узел и рукав в контексте сети соответственно. Массив Brs[]
обеспечивает нумерацию рукавов сети. JcInNet содержит массив номеров примыкаю-
щих к узлу рукавов BrNum[] («рукавный» идентификатор). Поэтому массив Jcs[] зада-
ёт структуру сети N . Операция Combine реализует цикл объединения всех узлов сети в один (167). При наличии в качестве аргумента указателя на объект класса Junc она ини-
циализирует его согласно результату объединения. Так как класс QuantNet не содержит в явном виде энергии электрона, он обеспечивает наиболее общий подход в расчётах по сетевой формуле.
Абстрактный класс Junc реализует основные операции с матрицами S , C и P про-
извольного узла: расчёт, сохранение, копирование. Операция расчёта S-матрицы FindS
