
Давыд Цуриков. Диссертация. 2015 г
..pdf11
Согласно таблице 2, минимальный и максимальный размеры рассматриваемых в дан-
ной работе систем Lmin и Lmax соответственно можно определить как
Llat |
Lmin |
λ |
(2) |
Llat |
Lmax |
< |
(3) |
Условие (2) обеспечивает применимость зонной теории к описанию наноструктуры, условие (3) делает доминирующим баллистический электронный транспорт через неё. Также для структур, удовлетворяющих свойству (2), является существенным размерное квантование носителей заряда.
Размерное квантование носителей заряда определяет тип структуры [4] (табл. 3).
Таблица 3. Квантовые структуры
разм. |
название |
|
Lx |
|
Ly |
|
Lz |
p |
M |
|
|
|
|
|
|
|
|
|
|
0D |
квантовая точка |
Lx |
~ λ |
Ly |
~ λ |
Lz |
~ λ |
– |
M ={sn} |
|
|
|
|
|
|
|
|
|
|
1D |
квантовая проволока |
Lx |
λ |
Ly |
~ λ |
Lz |
~ λ |
p = px |
M ={snp} |
|
|
|
|
|
|
|
|
|
|
2D |
квантовая плёнка |
Lx |
λ |
Ly |
λ |
Lz |
~ λ |
p ={px , py} |
M ={snp} |
|
|
|
|
|
|
|
|
|
|
3D |
объёмный кристалл |
Lx |
λ |
Ly |
λ |
Lz |
λ |
p ={px , py , pz} |
M ={sp} |
|
|
|
|
|
|
|
|
|
|
В таблице 3 Lx , Ly , Lz – размеры структуры вдоль осей X , Y , Z соответственно; p –
квазиимпульс; s =1,2 – спиновое квантовое число; n – квантовое число, отвечающее раз-
мерному квантованию. Размерность структуры – число направлений, в которых движение носителя заряда не ограничено. Размерность структуры равна размерности вектора квазиимпульса в мультииндексе одночастичного состояния M .
Применительно к системам в таблице 3 в литературе также используется термин «квазинизкоразмерная структура» [5]. Это актуально в случаях, когда математическая модель физической системы имеет размерность меньше трёх. Целесообразность такого приближения определяется спецификой конкретной задачи. Например, для квазиодномерной физической системы (квантовой проволоки) могут использоваться одно-, двух- и трёхмерные математические модели. В данной работе, в названиях структур приставка «квази-» опускается, а размерность модели конкретизируется в соответствующих разделах.
Каждую квантовую структуру в таблице 3 характеризует свой закон дисперсии и плотность одночастичных состояний. В качестве примера приведём данные характеристи-
12
ки для изотропной электронной подсистемы с квадратичной зависимостью энергии от квазиимпульса, взяв за начало отсчёта по энергии дно зоны проводимости (табл. 4).
Таблица 4. Характеристики электронной подсистемы квантовых структур
разм. |
закон дисперсии |
|
плотность состояний |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0D |
|
|
|
E |
M |
= E |
n |
|
g (E)= 2∑δ(En − E) |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
EM = En + |
p2 |
g (E)= |
L |
2m |
∑(E − En ) |
−1/2 |
|
|||||||||||||||
1D |
|
x |
x |
|
e |
[E > En ] |
||||||||||||||||||
|
2m |
|
|
|
|
|
π |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
n |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2D |
EM = En + |
|
px2 + py2 |
g (E)= |
Lx Lyme |
∑[E |
> En ] |
|||||||||||||||||
|
|
2m |
|
|
|
π |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
n |
|
|
|||
3D |
E |
|
= |
|
px2 |
+ py2 + pz2 |
g (E)= |
|
Lx Ly Lz |
2m |
3/2 |
E [E > 0] |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
||||||||
|
|
M |
|
|
|
|
|
2me |
|
|
|
2π2 |
|
|
2 |
|
|
|
||||||
В таблице 4 {En}n – уровни размерного квантования энергии электрона в структуре,
me – эффективная масса электрона, выражения записаны в нотации Айверсона [6, с. 42]:
скобки с утверждением равны 1, если оно истинно, и равны 0, если оно ложно. Поскольку здесь не учитывается спин-орбитальное взаимодействие, и отсутствует магнитное поле, в законе дисперсии нет явной зависимости от спинового квантового числа. За счёт этого суммирование по нему при вычислении плотности состояний согласно определению (1) даст дополнительный множитель 2. Суммирование по квазиимпульсу заменяется интегрированием, так как он принимает непрерывный ряд значений.
Из таблицы 4 видно, что за счёт размерного квантования меняется закон дисперсии носителей заряда. Это, в свою очередь, ведёт к изменению плотности состояний и, следовательно, к изменению термодинамических характеристик структуры.
На сегодняшний день особо актуальны низкоразмерные структуры на основе двумерного газа носителей заряда. Это связано с их перспективностью для наноэлектроники на базе планарной технологии. Данные системы также интересны возможностью их описания в рамках двумерных математических моделей, что существенно упрощает расчёты. Двумеризация носителей заряда в планарных полупроводниковых структурах является самостоятельной задачей и требует отдельного рассмотрения. Поэтому в разделе 1.2 данный процесс будет рассмотрен на примере квантового самосогласованного расчёта области пространственного заряда полупроводниковой плёнки.
13
1.2. Двумеризация носителей заряда в плёнке
Современные технологии позволяют формировать полупроводники с практически идеальной поверхностью (однородной, без поверхностных состояний и дефектов). В совокупности с высокоточными измерениями электрофизических характеристик это даёт возможность детально исследовать явление размерного квантования в области пространственного заряда (ОПЗ). В связи с этим возрастают требования к точности сопровождающих эксперимент расчётов.
История расчетов ОПЗ полупроводников с учетом размерного квантования носителей заряда насчитывает более 40 лет [7–18]. Исторически первый метод модельных потенциалов [7, 11–13] прост в реализации, но имеет низкую точность. Поэтому он малопригоден для количественного анализа результатов современных экспериментов. Для этих целей предпочтителен подход, основанный на самосогласованном решении уравнений Шрёдингера и Пуассона [8–17]. Однако его применение в режиме реального времени, в частности, при автоматизированном измерении проводимости в зависимости от поверхностного потенциала, имеет ряд трудностей. Они связаны с низкой скоростью расчётов и с неустойчивостью схемы в широких диапазонах значений параметров задачи. Для решения этих проблем нужны специальные алгоритмы вычислений на основе оптимальных численных методов.
1.2.1. Постановка самосогласованной задачи
Исходные уравнения
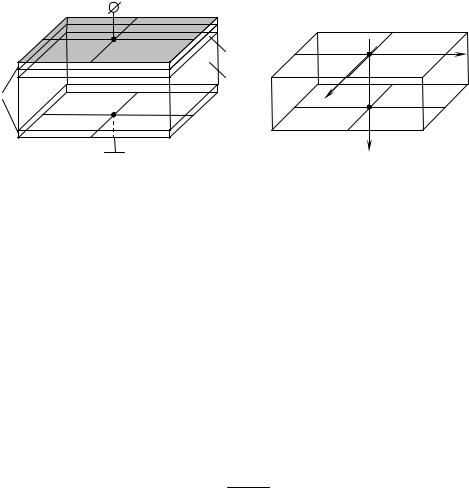
Рассмотрим однородно легированную полупроводниковую плёнку, предполагая отсутствие поверхностных состояний, полную ионизацию примесей и омический контакт с металлом на тыльной стороне (рис. 1). Приложенный к её лицевой стороне электростати-
ческий потенциал VS формирует в ней ОПЗ с поверхностной плотностью заряда
|
Q := ∫0L dzρ(z) |
|
(4) |
|
ρ(z) = e n |
−e n |
+e n+ (z) −e n− (z) |
(5) |
|
0 d |
0 a |
0 |
0 |
|
где ρ – объёмная плотность заряда; e0 – элементарный заряд; nd , na – концентрации ио-
низованных донорной и акцепторной примесей соответственно; n± – концентрации носителей заряда, здесь и всюду ниже в разделе 1.2 верхний индекс «–» отвечает электронам, «+» – дыркам.
14 |
|
|
|
a |
b |
|
|
top gate |
|
front side |
|
|
|
||
2 |
0 |
X |
|
3 |
|||
|
|
||
1 |
Y |
|
|
|
L |
|
|
rear side |
Z |
|
Рис. 1. Схематичное изображение полупроводниковой плёнки. a – плёнка в структуре с верхним затвором: 1 – металл, 2 – диэлектрик, 3 – полупроводник. b – расположение системы координат в плёнке, L – толщина плёнки.
Используя классическое приближение для описания движения носителей заряда в плоскости плёнки, выражения для их концентраций запишем в виде [10]
∞
n−(z) = n− ∑|ϕ−n (z) |2 F0 ([EF − EC − E−n ] / [k0T ])
n=1
∞
n+ (z) = n+ ∑|ϕ+n (z) |2 F0 ([EV − EF − E+n ] / [k0T ])
n=1
n± := m±k0T
π 2
(6)
(7)
(8)
где m± – эффективные массы носителей заряда в плоскости плёнки, k0 – постоянная Больцмана, T – температура кристалла, – постоянная Планка, F0 – интеграл Ферми– Дирака порядка 0 (см. приложение A), EF – уровень Ферми, EC и EV – энергии краёв зо-
ны проводимости и валентной зоны соответственно. Волновые функции носителей заряда
ϕ± и их уровни энергии E± можно найти из уравнения Шрёдингера:
|
2 |
2 |
|
± |
|
± |
± ± |
|
|
− |
|
∂z |
+U |
|
(z) |
ϕ |
(z) = E ϕ |
(z), |
z (0, L) |
2m± |
|
||||||||
|
|
|
|
|
|
|
|
|
(9) |
± |
(z) = 0, |
|
|
|
|
|
|
z {0, L} |
|
ϕ |
|
|
|
|
|
|
|||
|
|
|
|
|
U ± := ±e V |
|
(10) |
||
|
|
|
|
|
|
|
0 |
|
|
где m± – эффективные массы носителей заряда перпендикулярно плёнке, V – электроста-
тический потенциал.

15
Согласно (6)–(10), n± неявно зависят от V . Его можно найти из уравнения Пуассона:
|
′′ |
|
|
1 |
ρ(z), |
z (0, L) |
|
|
|||||
V |
(z) = − |
|
εε0 |
|||
|
|
|
|
|
(11) |
|
V |
(0) |
=V |
, V (L) = 0 |
|||
|
|
S |
|
|
|
|
где ε – диэлектрическая проницаемость плёнки, ε0 – электрическая постоянная. Потенци-
ал является самосогласованным, так как он определяет пространственное распределение концентраций носителей заряда в плёнке и при этом зависит от него.
Самосогласованный расчёт потенциала V осуществляется следующим образом. На первой итерации задаётся потенциал V1 , как результат численного решения уравнения Пу-
ассона в классическом приближении [19]. На основе V1 вычисляется объёмная плотность заряда ρ1 согласно (5)–(9). Следующие итерации организуются по схеме
|
V |
= |
1 |
|
(V +V |
) |
|
|
|
||||||
|
n+1 |
2 |
|
n n+1 |
|
||
Vn′′+1 |
(z) = − |
|
1 |
|
ρn (z), |
z (0, L) |
|
εε0 |
|
||||||
|
|
|
|
|
|
||
Vn+1 |
(0) =VS , |
|
Vn+1(L) = 0 |
||||
Интегрируя правую часть уравнения (13) с учётом граничных условий, получим
V + (z) =V + ∫L dz E (z ) −V z − ∫z dz E (z )
n 1 S 0 1 n 1 S L 0 1 n 1
En (z) := εε10 ∫0z dz1ρn (z1)
Специфика квантового самосогласованного расчёта
(12)
(13)
(14)
(15)
Перед квантовым самосогласованным расчётом ОПЗ найдём уровень Ферми в плёнке из уравнения электронейтральности:
Q = 0, VS = 0 |
(16) |
С учётом (4)–(7) и нормировки волновых функций
∫L dz |ϕ± (z) |2 =1, n N (17)
0 n
поверхностная плотность заряда примет вид

16
|
∞ |
([EV − EF − E+n ] / [k0T ]) |
|
Q = e0 (nd −na )L +e0n+ ∑F0 |
|||
|
n=1 |
(18) |
|
∞ |
|
||
([EF − EC − E−n ] / [k0T ]) |
|||
− e0n− ∑F0 |
|||
n=1
Согласно (18), уравнение (16) является самосогласованным: при VS = 0 потенциал в плён-
ке отличен от нуля. Это приводит к изгибу зон [7] и отклонению уровней энергии {E±n}∞n=1
от уровней энергии прямоугольной потенциальной ямы:
2
E± := (πn / L)2 , n N (19)
n 2m±
Как показали расчёты, на положение уровня Ферми этот эффект влияет слабо. Поэтому,
полагая E±n ≈ E±n , с учётом (16), (18) и (19) для поиска EF можно использовать прибли-
жённое уравнение электронейтральности:
|
∞ |
([EV − EF − E+n ] / [k0T ])− |
|
0 = e0 (nd −na )L +e0n+ ∑F0 |
|||
|
n=1 |
(20) |
|
∞ |
|
||
([EF − EC − E−n ] / [k0T ]) |
|||
− e0n− ∑F0 |
|||
n=1
Оно позволяет повысить скорость вычислений в силу отсутствия самосогласования при поиске уровней энергии.
В численных расчётах для концентраций носителей заряда вместо выражений (6) и (7) используются
nK−
nK+
K |
F0 ([EF − EC − E−n ] / [k0T ]) |
|
(z) := n− ∑| ϕ−n (z) |2 |
(21) |
|
n=1 |
|
|
K |
F0 ([EV − EF − E+n ] / [k0T ]) |
|
(z) := n+ ∑|ϕ+n (z) |2 |
(22) |
n=1
Верхние пределы суммирования находим, удваивая K , пока не будет выполнено условие
| Q± |
−Q± |
|<δ |
Q |
| Q± |
| |
(23) |
K |
K /2 |
|
K /2 |
|
|
|
QK± := ±e0 |
∫0L dznK± (z) |
|
(24) |
|||
где δQ – заданная относительная погрешность вычисления поверхностной плотности за-
ряда. Конечное значение K может быть различным для электронов и дырок. Это связано с особенностями расположения их уровней энергии при данном потенциале. Предложенный подход позволяет ограничиться расчётом только тех уровней энергии, которые сущест-
17
венно влияют на заряд в ОПЗ. В результате выражение для объёмной плотности заряда в (15) примет вид
ρ ≈ e (n |
−n ) +e n+ |
−e n− |
(25) |
|
0 d |
a |
0 K |
0 K |
|
По аналогии с (23) запишем условие выхода их самосогласованной процедуры:
| QM −QM −1 |<δQ | QM −1 | |
(26) |
где QM – поверхностная плотность заряда, рассчитанная на M-й итерации.
1.2.2. Расчёт уровней энергии носителей заряда
Безразмерная задача
В основе самосогласованной процедуры расчёта лежит численное решение задачи (9). Запишем её в безразмерном виде. Введём безразмерную координату и толщину плёнки
ξ := z / LD , λ := L / LD |
(27) |
где LD – длина дебаевского экранирования [19], энергию и потенциал
ε := 2m± |
−2L2 |
E±, |
|
|
|
|
D |
|
(28) |
υ(ξ) := 2m± |
|
|
||
−2 L2 U ± (L ξ), |
||||
|
|
|
D |
D |
волновые функции ψ с нормировкой
∫0λ dξ |ψ (ξ) |2 =1 |
(29) |
Из (17), (27) и (29) получим
ϕ± (z) = L−1/2ψ (z / L ) |
(30) |
||
|
D |
D |
|
Согласно (27) имеем
∂ |
z |
= L−1∂ |
ξ |
(31) |
|
D |
|
Тогда безразмерная задача на собственные функции и собственные значения примет вид
|
2 |
+υ(ξ)]ψ (ξ) = εψ (ξ), |
ξ (0,λ) |
(32) |
[−∂ξ |
||||
ψ (ξ) = 0, |
ξ {0,λ} |
|
||
Задачу (32) будем решать методом стрельбы [20]. Он состоит в решении задачи Коши, поставленной на одном конце интервала (0,λ) , и поиске таких значений ε , при которых выполняется граничное условие на другом конце. Потенциал в (32) является монотонным.
18
Стрельба со стороны его максимального значения υmax := max υ(ξ) в сторону минималь-
ξ (0,L)
ного υmin := min υ(ξ) даст лучшее выполнение граничного условия. Перед переходом от
ξ (0,L)
(9) к (32) применим правило смены системы координат
z |
z, |
|
±VS |
≤ 0 |
(33) |
|
− z, |
±VS |
> 0 |
||
|
L |
|
Тогда потенциал в (32) всегда будет возрастающим, и стрельба будет из точки ξ = λ в
точку ξ = 0 (справа налево).
Численное решение задачи Коши
Рассмотрим состояния носителя заряда с энергией υmin < ε <υmax . Их волновые функ-
ции под потенциальным барьером быстро спадают и вблизи точки ξ = λ могут оказаться пренебрежимо малыми. Организуем алгоритм формального смещения правой границы и выбора на ней значения производной волновой функции в задаче Коши. Это позволит повысить скорость и устойчивость расчётов.
В основе подхода лежит аппроксимация волновой функции в интервале под барьером
[ξ+,λ] , где ξ+ – правая точка поворота: υ(ξ+ ) = ε , ε – начальное приближение к собст-
венному значению ε . Для оценки её скорости спада усредним нулевое квазиклассическое приближение [21]:
ψ (ξ) = Dsh(κ |
[λ −ξ]) |
(34) |
||||||||||
κ |
:= |
1 |
∫ξλ+ dξκ(ξ) |
(35) |
||||||||
λ −ξ+ |
||||||||||||
|
|
κ(ξ) := |
|
υ(ξ) −ε |
(36) |
|||||||
Положив ψ′(ξ+ ) =1, найдём неизвестную константу D и из (34) получим |
|
|||||||||||
|
′ |
−1 |
|
|
|
|
|
|
||||
|
(κ[λ −ξ+ ]) |
(37) |
||||||||||
ψ (λ) = ch |
|
|
||||||||||
Условием большой толщины положим |
|
|
|
|
|
|
|
|
||||
|
|
κ |
[λ −ξ+ ] > |
1 |
exp |
(38) |
||||||
|
|
2 |
||||||||||
где exp – максимальный показатель экспоненты для данной ЭВМ, коэффициент |
1 |
полу- |
||||||||||
2 |
||||||||||||
чен эмпирически. При выполнении (38) новое положение правой границы λ< найдём из уравнения

19
κ |
[λ −ξ |
+ |
] = |
1 |
exp |
|
|||||
< |
2 |
||||
Тогда для выбора λ< получим правило
λ, |
|
|
|
|
|
|
κ |
[λ −ξ+ ] ≤ |
1 |
|
exp |
||
|
|
|
|
|
|
2 |
|||||||
λ< = |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ξ+ |
+ |
exp |
/ κ, |
κ[λ −ξ+ ] > |
|
exp |
|||||||
2 |
2 |
|
|||||||||||
При этом полагаем
ξ [λ< ,λ] ψ (ξ )= 0
Таким образом, для решения задачи (32) методом стрельбы имеем задачу Коши:
|
2 |
+υ(ξ)]ψ (ξ) = εψ (ξ), |
|
ξ (0,λ< ) |
|||||||||
[−∂ξ |
|
||||||||||||
|
|
|
′ |
|
−1 |
|
|
|
|
|
|
|
|
ψ (λ ) = 0, |
|
(κ |
|
|
[λ |
−ξ |
|
]) |
|||||
ψ (λ ) = ch |
|
< |
+ |
||||||||||
|
< |
|
|
< |
|
|
|
< |
|
|
|||
κ< := λ< 1−ξ+ ∫ξλ+< dξκ(ξ)
(39)
(40)
(41)
(42)
(43)
При υmin < ε <υmax выбираем предварительно положение правой границы согласно (40) с
учётом (35) и (36), а при υmax ≤ ε |
полагаем в (42) λ< = λ и ψ′(λ< ) =1. |
|
|
Для повышения скорости |
решения задачи Коши выберем сетку из N |
узлов |
|
{ξ }N |
[0,λ ] с постоянным шагом h |
|
|
n n=1 |
< |
|
|
|
|
ξn −ξn−1 =: h, n = 2,..., N |
(44) |
Корректный вид волновых функций в широком диапазоне значений ε (устойчивость) обеспечит алгоритм Верле в скоростной форме. При стрельбе справа налево в задаче (42) на правой границе сетки имеем
|
|
′ |
−1 |
|
|
|
|
|
ψN = 0, |
ψN = ch |
(κ<[λ< −ξ+ ]), |
(45) |
|||||
|
||||||||
′′ |
= (υN |
−ε)ψN = 0 |
||||||
|
||||||||
ψN |
|
|||||||
а значения функции и её производных в прочих узлах сетки вплоть до левой границы находим последовательно по схеме
|
|
′ |
1 |
′′ |
2 |
→ |
|
2 |
|
|
|||||
ψn−1 =ψn −ψnh + |
ψnh |
|
|
||||
ψn′′−1 = (υn−1 −ε)ψn−1 |
|
→ |
(46) |
||||
ψn′−1 =ψn′ − |
1 |
(ψn′′−1 +ψn′′)h |
|
|
|||
2 |
|
|
|||||
где ψn :=ψ (ξn ) , υn :=υ(ξn ) .

20
Поиск уровней энергии
В методе стрельбы следует найти нули ψ (0) , как функции параметра ε : {ε |
}∞ |
. Для |
||||
|
|
|
|
|
n n=1 |
|
их быстрого поиска получим приближения к ним {ε |
}∞ |
. |
|
|
|
|
|
n n=1 |
|
|
|
|
|
Из квазиклассического условия квантования [21] найдём {ε |
}3 |
: |
|
|
||
|
|
|
n n=1 |
|
|
|
∫0ξ+ dξ εn −υ(ξ) =πn −π / 4, n =1,2,3 |
|
|
(47) |
|||
Уравнение (47) – задача на поиск нуля функции, у которой он только один. Его можно
легко найти: ε1 (υmin ,υmax +π 2 / λ2 ] , для ε2 и ε3 начальные приближения – ε1 и ε2 |
соот- |
|||
ветственно. |
|
|
|
|
Для расчёта {ε |
}∞ |
экстраполируем ε , как функцию квантового числа n , по извест- |
||
|
n |
n=4 |
|
|
ным εn−3 , εn−2 , εn−1 |
|
в область следующего уровня энергии: |
|
|
|
|
|
εn = A + Bn +Cn2 |
(48) |
Записав (48) для εn−3 , εn−2 , εn−1 , найдём неизвестные коэффициенты и получим
εn |
= εn−1 + B +C(2n −1), n > 3 |
|
||||
B |
= ( |
5 |
−n)(εn−1 −εn−2 ) +(n − |
3 |
)(εn−2 −εn−3 ) |
(49) |
2 |
2 |
|||||
C= 12 (εn−1 −2εn−2 +εn−3 )
Сростом n точность локализации (49) повышается, так как зависимость энергии от квантового числа стремится к параболической.
Резюме
Таким образом, схема решения задачи (9) состоит в следующем:
•с учётом правила (33) переход от размерной задачи (9) к безразмерной (32) согласно
(27)–(31);
•локализация уровней энергии посредством (47), (49);
•уточнение их положения с помощью метода Ньютона, применённого к методу стрельбы в задаче (42);
•восстановление размерных уровней энергии и волновых функций на основе безразмерных согласно (28), (30) с учётом нормировки (29) и правила (33).
