
Давыд Цуриков. Диссертация. 2015 г
..pdf
|
|
|
111 |
|
|
|
|
|
|
|
Ψ(x, y, z)= ∑m gm (x)hm (y, z), |
|
gm := hm Ψ |
|
|
(307) |
|||||
|
2 |
2 |
= λmhm , in |
Β |
= |
|
|
|
||
[−∂y −∂z ]hm |
|
|
|
(308) |
||||||
hm = 0, |
|
|
on ∂Β= |
|
|
|||||
|
|
|
|
|
||||||
(306) 0 =[− −ε +υ] Ψ = ∑mn hm |
|
2 |
2 |
2 |
|
|
hn |
Ψ ; (307), (308) |
|
|
hm −∂1 −∂ |
2 −∂3 |
−ε +υ hn |
||||||||
∑n (−Imn∂12 +Vmn )gn = ∑n Emn gn , |
Vmn := hm |
υ hn , Emn := Imn (ε −λm ) |
(309) |
|||||||
Решение системы (309) можно записать в виде: |
|
|
|
|
|
|
||||
gm (x)= ∑n gmn◊1 (x)cn◊1 +∑n gmn◊2 (x)cn◊2 g = g◊c◊ |
(310) |
|||||||||
где g◊1 , g◊2 – матрицы фундаментальной системы решений (ФСР) задачи (309):
∑n (−Imn∂12 +Vmn )gnk◊ |
= ∑n Emn gnk◊ |
, x (−a, +a) |
g◊◊11 |
g |
◊◊ |
22 |
(x)≠ 0 |
(311) |
|
|
|
|
|
g |
g |
|
|
|
|
(307), (310) W k Ψ = ∑n hnk |
hnk W k Ψ = ∑lnmp hnk |
hnk W k g◊pml cm◊l hp |
|
=: ∑lnm Gnm◊klcm◊l hnk |
|
||||
W k Ψ = ∑n[G◊c◊]nk hnk , |
Gnm◊kl = ∑p |
hnk W k g◊pml |
hp |
|
|
|
(312) |
||
Оператор G◊ в (312) полностью соответствует определению (118). Его также можно записать в матричном виде по рукавам:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
◊ |
|
|
◊ |
(−x −a) |
|
◊kl |
k |
◊l |
k |
|
k |
|
|
|
k |
◊l |
|
k |
k |
|
W |
g pm |
(x)= g pm |
|
||||||||
Gnm |
= ∑p W |
gpm |
|
hn |
W |
|
hp |
= ∑p W |
g pm |
|
W |
|
hn |
hp ; |
W 2 g◊ |
(x)= g◊ (+x + a) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pm |
|
|
pm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Gnm◊ (x)= ∑p |
g◊pm1 |
(−x −a) W1hn1 hp |
g◊pm2 (−x −a) |
W1hn1 hp |
|
|
|||||||||||||||||
|
|
|
|
◊1 |
(+x + a) W |
2 |
2 |
|
|
◊2 |
(+x + a) |
|
2 |
2 |
|
(313) |
||||||||||
|
|
|
|
|
|
|
|
|
|
hp |
W |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
g pm |
|
hn |
gpm |
|
hn hp |
|
|
||||||||||
Помимо поперечного сечения проволоки, скалярные произведения в (313) также определяет выбор ЛСК в конкретной задаче. В простейшем случае, когда они связаны друг с другом отражением относительно плоскости YZ , имеем W 1hn1 = hn =W 2hn2 , и выражение
(313) примет вид
G |
◊ |
gnm◊1 |
(−x −a) |
gnm◊2 (−x −a) |
(314) |
|
(x)= |
(+x + a) |
|
||
nm |
gnm◊1 |
gnm◊2 (+x + a) |
|
||
Наконец, необходимые для расчётов матрицы ФСР {g◊k }k=1,2 можно найти численно,
например, решив задачи Коши:
|
|
|
|
112 |
|
|
|
2 |
|
◊k |
◊k |
∑p −Imp |
∂x |
+Vmp (x) g pn (x)= ∑p |
Emp gpn (x), x (−a, +a) |
||
|
(−a)= Imn1k , |
∂1gmn◊k (−a)= Imn2k |
(315) |
||
gmn◊k |
|
||||
|
|
|
|
|
|
Таким образом, трёхмерная задача рассеяния на неоднородности в квантовой проволоке (306) сводится к системе обыкновенных дифференциальных уравнений. Рассчитав матрицы фундаментальной системы решений через (315), можно записать оператор G◊ (312). С его помощью можно найти коэффициенты разложения для функции Ψ в (307), (310) и S-матрицу I-узла посредством (120) и (121) соответственно.
Двумерный I-узел
Двумерная математическая модель квантовой проволоки актуальна для структур, сформированных на базе двумерного электронного газа. Как и в трёхмерном случае здесь сохраняется специфика (305) для рукавов с поперечными сечениями в виде интервалов {βk = (0,b)}k=1,2 . Также выберем ГСК такую, что Β= = (0,b) . Тогда с учётом свойства (305)
в терминах ГУР (107) задача рассеяния электрона в носителе финитного потенциала (I- узле) Ω = (−a,+a)×(0,b) примет вид:
− +υ |
(x, y) Ψ(x, y)= εΨ(x, y), |
{x, y} (−a,+a)×(0,b) |
|
|
|
x (−a,+a) |
(316) |
Ψ(x,0)= Ψ(x,b)= 0, |
|||
(K +i∂1 )W Ψ(0, y)= 2Kψ (0, y), |
y (0,b) |
|
|
|
|
|
|
|
|
|
|
Как и в трёхмерном случае, ищем решение задачи (316) в виде разложения по орто-
нормированной системе {hm}m :
Ψ(x, y)= ∑m gm (x)hm (y), |
gm := hm Ψ |
(317) |
|
|
2 |
y (0,b) |
|
−∂yhm (y)= λmhm (y), |
(318) |
||
hm (y)= 0, |
y {0,b} |
||
|
|
|
|
Последующие выкладки с точностью до понижения размерности аналогичны выкладкам, следующим за (308). Поэтому здесь также верны выражения (309)–(315).
Для двумерных систем зачастую удобно использовать ЛСК, связанные друг с другом поворотом и трансляцией (рис. 17). Выясним, как при этом будет выглядеть выражение для оператора G◊ (313).

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
113 |
|
|
|
|
|
|
|
|
||
|
1 |
(x, y)= (−x −a,b − y) |
|
W |
1 |
◊ |
◊ |
− a)hm (b − y) |
|
|
|
|||||||||||||||||||
w |
|
|
|
gm (x)hm (y)= gm (−x |
|
|
|
|||||||||||||||||||||||
w2 |
(x, y)= (+x |
+ a, y) W 2 gm◊ (x)hm (y)= gm◊ ( |
+x + a)hm (y) |
|
|
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
1 |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
W |
|
W |
=W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
hm |
= hm = hm , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
▲ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{υk |
|
= |
0}k=1,2 |
|
hmk (y)= |
|
2 |
sin (πbm y) W1hm1 |
(y)= |
|
2 |
sin (πbm [b − y])= |
|
|
||||||||||||||||
|
|
b |
b |
|
||||||||||||||||||||||||||
|
|
= |
|
|
2 |
sin (πbm b)cos(πbm y) |
−cos(πbm b)sin (πbm y) = |
(−1)m+1 hm1 (y) |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
b |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1hn1 = (−1)n+1 hn1 , W |
2hn2 = hn1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|||||||||||
Выберем ГСК так, что h = h1 |
. Тогда |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(313), (319) |
|
Gnm◊ (x)= (−1)n+1 gnm◊1 (−x −a) |
(−1)n+1 gnm◊2 (−x −a) |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
gnm◊1 (+x + a) |
|
|
gnm◊2 (+x + a) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(319)
(320)
Таким образом, двумерная задача рассеяния на неоднородности в квантовой проволоке (316) сводится к системе обыкновенных дифференциальных уравнений. Рассчитав мат-
рицы фундаментальной системы решений через (315), можно записать оператор G◊ (312). С его помощью можно найти коэффициенты разложения для функции Ψ в (317), (310) и S-матрицу I-узла посредством (120) и (121) соответственно.
Одномерный I-узел
Простейшей математической моделью квантовой проволоки является одномерная модель. Она описывает движение электрона в единственном канале, энергия которого принимается равной нулю. В силу своей специфики данная модель имеет ограниченную область применения и даёт представление о транспортных свойствах квантовой проволоки на качественном уровне. Для одномерного случая
{hk }k=1,2 |
={1,1}, {K kl = I klκl ,κl = ε}k ,l=1,2 |
(321) |
n n |
|
|
Тогда с учётом (100) в терминах ГУР (107) задача рассеяния электрона в носителе финитного потенциала (I-узле) Ω = (−a,+a) примет вид:
|
2 |
|
Ψ(x)= εΨ(x), |
x (−a,+a) |
|
−∂x |
+υ(x) |
(322) |
|||
[K +i∂1 ]W Ψ |
(0)= 2Kc |
|
|||
|
|
|
|
|
|
Решением задачи (322) является линейная комбинация двух линейно независимых решений уравнения на Ψ в (322):
Ψ(x)= g◊1 (x)c◊1 + g◊2 (x)c◊2 = ∑k g◊k (x)c◊k |
(323) |
114
(323) W k Ψ =W k ∑l g◊lc◊l = ∑l W k g◊lc◊l |
|
|
|
|
|
|
|
||||
|
|
W k Ψ =[G◊c◊]k , |
G◊kl :=W k g◊l |
|
(324) |
||||||
С учётом (321) оператор G◊ в (324) полностью соответствует определению (118). Его |
|||||||||||
также можно записать в матричном виде: |
|
|
|
|
|
|
|
||||
|
|
W1g◊1 (x) W1g◊2 (x) |
|
|
|
|
|||||
G◊kl =W k g◊l |
|
G◊ (x)= W 2 g◊1 (x) W 2 g◊2 |
(x) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(w1 )−1 x = −x −a w1x = −x − a W1g◊ (x)= g◊ (w1x) = g◊ (−x − a) |
|||||||||||
(w2 )−1 x = +x −a |
w2 x = +x + a W 2 g◊ (x)= g◊ (w2 x) |
= g◊ (+x + a) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
◊1 |
(−x |
−a) |
g |
◊2 |
(−x −a) |
|
(325) |
|
|
|
G◊ (x)= g |
|
|
|
||||||
|
|
g◊1 (+x + a) |
g◊2 (+x + a) |
|
|||||||
Функции g◊k можно найти численно, например, решив две задачи Коши:
|
2 |
|
◊k |
(x)= εg |
◊k |
(x), x (−a, +a) |
|
−∂x |
+υ(x) g |
|
|
(326) |
|||
g◊k (−a)= I1k , |
|
∂1g◊k (−a) |
= I 2k |
||||
|
|
||||||
|
|
|
|
|
|
|
|
Таким образом, одномерная задача рассеяния на неоднородности в квантовой проволоке (322) сводится к линейной комбинации двух функций. Рассчитав два линейно неза-
висимых решения через (326), можно записать оператор G◊ (325). С его помощью можно найти коэффициенты разложения для функции Ψ в (323) и S-матрицу I-узла посредством (120) и (121) соответственно.
Приложение C. S-матрица квантовой сети
втерминах DN- и ND-map
Вподразделе 2.1.2 в рамках обзора методов расчёта S-матрицы квантовой сети был представлен метод DN- и ND-map. Далее в подразделе 2.2.3 он был конкретизирован для используемой системы обозначений (подраздел 2.2.1). В этом приложении приведено математическое сопровождение к нему. Также здесь представлен метод промежуточных DN-
иND-map [23, 24, 32–34]. Идентификатор узла здесь редуцирован для краткости.
Классические DN- и ND-map
Получим выражение для расширенной матрицы рассеяния в терминах классического
DN-map (122). Из (125), (98)–(100)
|
|
|
|
|
|
|
|
|
|
|
115 |
|
|
0 = ∑l Dkl ψ l (0,...) |
− ∂1ψ k (0,...) |
= |
|
|
|
|
|
||||||
= ∑lmn hml |
|
hml Dkl |
hnl |
|
hnl ψ l (0,...) |
−∑m |
hml hml |
∂1ψ k (0,...) |
= |
||||
l |
|
l kl |
|
l |
l |
(0,...) |
− |
l |
k |
(0,...) |
|
|
|
= ∑m hm |
∑n Dmn hn |
ψ |
hm ∂1ψ |
|
|
|
|||||||
0 = ∑ln Dmnkl |
hnl |
ψ l (0,...) |
− hmk ∂1ψ k (0,...) = |
|
|
|
|
||||||
= ∑ln Dmnkl |
hnl ∑p [c |
+ Sc ]lphpl |
− hmk ∑n [−iKc |
+iKSc ]nk hnk |
= |
||||||||
= ∑ln Dmnkl |
[c |
+ Sc ]ln −[−iKc |
+iKSc ]mk |
|
|
|
|||||||
O = D[c + Sc ]+iKc −iKSc |
=[D +iK ]c |
+[D −iK ]Sc |
|
||||||||||
|
|
|
|
|
|
|
|
|
S =[iK − D]−1[iK + D] |
(327) |
|||
Получим выражение для расширенной матрицы рассеяния в терминах классического
ND-map (123). Из (125), (98)–(100)
0 = ∑l N kl ∂1ψ l (0,...) |
− ψ k (0,...) |
= |
|
|
|
|
|
|
||||||
= ∑lmn hml |
hml |
N kl |
hnl |
hnl |
∂1ψ l (0,...) −∑m |
hml |
hml ψ k (0,...) |
= |
||||||
l |
|
l |
kl |
l |
∂1ψ |
l |
|
l |
l |
ψ |
k |
|
|
|
= ∑m hm |
∑n |
Nmn |
hn |
|
(0,...) − hm |
hm |
|
(0,...) |
|
|||||
0 = ∑ln Nmnkl |
hnl |
∂1ψ l (0,...) |
− hmk ψ k (0,...) |
= |
|
|
|
|
|
|||||
= ∑ln Nmnkl |
hnl |
∑p [−iKc +iKSc ]lp hpl − hmk |
∑n [c + Sc ]nk hnk |
= |
||||||||||
= ∑ln Nmnkl |
[−iKc +iKSc ]ln −[c |
+ Sc ]mk |
|
|
|
|
|
|||||||
O = N [−iKc |
+iKSc ]−c |
− Sc = −[NiK + I ]c +[NiK − I ]Sc |
|
|||||||||||
|
|
|
|
|
|
|
|
S =[NiK − I ]−1[NiK + I ] |
(328) |
|||||
Выражения (327) и (328) эквивалентны с учётом свойства |
||||||||||||||
|
|
|
|
|
|
|
|
DN = I = ND |
|
(329) |
||||
Промежуточные DN- и ND-map
Согласно (224) и (198), токи через квантовую сеть зависят только от блока расширен-
ной матрицы рассеяния, который связывает амплитуды волн в открытых каналах: S++
(«стандартная» матрица рассеяния). Для S++ можно записать выражения со структурой аналогичной формулам (327) и (328) в терминах промежуточных DN- и ND-map [23, 24].
Получим выражение для «стандартной» матрицы рассеяния в терминах промежуточ-
ного DN-map. Из (327)
[iK − D]S = iK + D
116
iK++ − D++ |
|
−D+− |
S++ |
S+− |
iK++ + D++ |
|
D+− |
|
|
||||||
|
−D |
iK |
−− |
− D |
S |
−+ |
S |
|
= |
D |
iK |
−− |
+ D |
|
|
|
−+ |
|
−− |
|
−− |
|
−+ |
|
−− |
|
|||||
(iK++ − D++ )S++ − D+−S−+ = iK++ + D++ |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
−D−+S++ +(iK−− − D−− )S−+ = D−+ S−+ = (iK−− − D−− )−1 D−+ (I + S++ ) |
|
||||||
|
|
|
|
|
|
|
|
(iK++ − D++ )S++ − D+− (iK−− − D−− )−1 D−+ (I + S++ )= iK++ + D++ |
|
||||||
|
−1 |
|
−1 |
|
|
|
|
iK++ − D++ − D+− (iK−− − D−− ) |
D−+ S++ = D+− (iK−− − D−− ) |
D−+ |
+iK++ + D++ |
||||
|
|
||||||
|
|
S++ = (iK++ − M++ )−1 (iK++ + M++ ) |
|
(330) |
|||
|
M++ := D++ + D+− (iK−− − D−− )−1 D−+ |
|
(331) |
||||
M++ – промежуточный DN-map (intermediate DN-map). |
|
|
|
|
|||
Получим выражение для «стандартной» матрицы рассеяния в терминах промежуточ-
ного ND-map. Из (328)
[NiK − I ]S = NiK + I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
N++ |
N+− iK++ |
O+− N++iK++ |
N+−iK−− |
|
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||||||||
NiK = N |
−+ |
N |
O |
iK |
|
= N |
−+ |
iK |
++ |
N |
−− |
iK |
|
|
|
|
|
|
||||
|
|
|
−− |
−+ |
|
−− |
|
|
|
|
|
−− |
|
|
|
|
||||||
N++iK++ − I++ |
|
N+−iK−− |
|
|
S++ |
S+− = N++iK++ + I++ |
N+−iK−− |
|
|
|||||||||||||
|
N−+iK++ |
|
N−−iK−− − I−− S−+ |
S−− |
|
|
N−+iK++ |
|
N−−iK−− + |
I−− |
|
|||||||||||
(N++iK++ − I++ )S++ + N+−iK−−S−+ = N++iK++ |
+ I++ |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S−+ = (N−−iK−− − I−− )−1 |
N−+iK++ (I++ − S++ ) |
|||||||
N−+iK++S++ +(N−−iK−− − I−− )S−+ = N−+iK++ |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(N++iK++ − I++ )S++ + N+−iK−− (N−−iK−− − I−− )−1 N−+iK++ (I++ − S++ )= N++iK++ + I++ |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
N++iK++ − I++ − N+−iK−− (N−−iK−− − I−− ) |
N−+iK++ S++ = |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||
= N++iK++ + I++ − N+−iK−− (N−−iK−− − I−− )−1 N−+iK++ |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
S++ = (L++iK++ − I++ )−1 (L ++iK++ + I++ ) |
|
(332) |
|||||||||||||
|
|
|
|
|
|
L++ := N++ − N+−iK−− (N−−iK−− − I−− )−1 N−+ |
|
(333) |
||||||||||||||
L++ |
– промежуточный ND-map (intermediate ND-map). |
|
|
|
|
|||||||||||||||||
|
Выражения (330) и (332) эквиваленты с учётом свойства |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
M++L++ = I++ = L++M++ |
|
|
(334) |
||||||||||
Промежуточные DN- и ND-map также можно найти напрямую путём решения уравнения Шрёдингера со специальными граничными условиями [23].
117
Актуальность и применимость
Актуальность и применимость двух типов DN- и ND-map определяются решаемой задачей. Как было отмечено выше, для расчёта токов через квантовую сеть достаточно най-
ти её «стандартную» матрицу рассеяния S++ в приемлемом для приближённого интегри-
рования диапазоне энергий (224). К решению этой задачи есть два подхода.
1. Сеть – единый узел. Если рассматривать всю сеть как единый узел, соединённый непосредственно с резервуарами, то достаточно рассчитать матрицу S++ только данного узла. В этом случае может быть актуальным метод промежуточных DN- и ND-map, позволяющий использовать выражения (330) и (332).
2.Сеть – система узлов. Если рассматривать сеть как совокупность соединённых друг
сдругом узлов, то её матрица S++ берётся в виде блока её расширенной матрицы рассея-
ния, рассчитанной по сетевой формуле (167). В общем случае сетевая формула корректна при объединении только расширенных матриц рассеяния узлов, образующих сеть. Следовательно, для отдельных узлов приемлем метод только классических DN- и ND-map, позволяющий использовать выражения (327) и (328).
Преимущество подхода 1 – упрощённая формулировка задачи. Однако для сетей, состоящих из большого количества узлов, с точки зрения расчётов, эффективнее подход 2. Это связано с тем, что при вычислениях в подходе 2 достаточно найти расширенные матрицы рассеяния типовых узлов сети. В результате при прямых расчётах выполняется триангуляция только типовых узлов, в то время как в подходе 1 требуется провести триангуляцию всей сети, включая её внутренние рукава.
В настоящей диссертации для расчёта токов через квантовую сеть использовался подход 2. Поэтому метод промежуточных DN- и ND-map для неё был заведомо неприменим, и в дополнение к методу ГУР для расчёта расширенных матриц рассеяния узлов использовался метод классического ND-map.
Приложение D. Примеры расчёта S-матриц по сетевой формуле
В этом приложении сетевая формула (167) проиллюстрирована расчётами S-матриц участков сети различной структуры [А3].
Общий случай
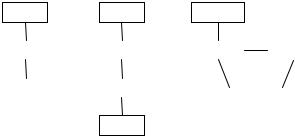
Рассмотрим участки квантовой сети, изображённые на рисунке 26. Геометрии узлов и рукавов положим произвольными в рамках поставленной выше задачи. Для простоты рас-
118
смотрим случай, когда ЛСК на концах каждого внутреннего рукава связаны друг с другом отражением: U [J,K]KK = I KK =U[J,K]KK .
a |
b |
|
|
|
c |
|
|
|||
Ω[...,1] |
Ω[...,1] |
Ω[...,1] |
|
|
|
|
|
|||
1 |
|
1 |
|
1 |
|
|
2 |
|
|
|
Ω[1,2] |
|
Ω[1,2] |
|
Ω[1,2,3] |
|
|
Ω[2,4] |
|||
2 |
|
2 |
|
3 |
|
|
|
|
|
4 |
Ω[2] |
|
Ω[2,3] |
|
|
|
Ω[3,4] |
|
|
||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Ω[3,...] |
|
|
|
|
|
|
|
|
Рис. 26. Схемы участков квантовой сети: a – замкнутый участок, b – последовательный участок, c – участок с ветвлением.
Рассмотрим замкнутый участок |
квантовой сети (рис. 26a). |
Для |
него |
E ={1}, |
||||||||||||||
N ={{1,2},{2}}. Сетевая формула (167) примет вид: |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
S[1] = S[1,2] S[2] |
|
|
|
|
|
|
|
(335) |
||
Раскрывая (335) по формуле (160) с учётом того, что J ={1}, K ={2}, L = , имеем |
||||||||||||||||||
|
[1] |
|
[1,2]11 |
|
[1,2]12 |
12 |
|
|
−S[1,2]22 |
|
exp(−iK 22 A22 ) −1 |
S[1,2]21 |
|
|||||
S |
= S |
|
|
|
|
|
|
|
|
|
21 |
(336) |
||||||
|
|
+ S |
|
O |
|
|
22 |
22 |
|
[2]22 |
|
|
O |
|||||
|
|
|
|
|
|
|
|
|
) |
−S |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
exp(−iK A |
|
|
|
|
|
|||||
Для последовательного участка сети (рис. 26b) E ={1,3} , N ={{1,2},{2,3}} . Согласно
(167), его S-матрица запишется как
S[1,3] = S[1,2] S[2,3] |
(337) |
Полагая J ={1}, K ={2}, L ={3}, с помощью (160) раскроем формулу (337):
|
|
[1,2]11 |
|
13 |
|
|
|
|
[1,2]12 |
12 |
|
|
|
|
|
|
||
S[1,3] = S |
|
O |
|
|
|
+ S |
|
|
O |
× |
|
|
|
|
||||
|
O31 |
S[2,3]33 |
|
|
O32 |
|
S[2,3]32 |
|
|
|
|
|
(338) |
|||||
|
|
−S[1,2]22 |
|
|
exp(−iK 22 A22 ) |
−1 |
S[1,2]21 |
O23 |
||||||||||
|
|
|
|
|
||||||||||||||
× |
|
|
|
22 |
|
22 |
) |
|
|
[2,3]22 |
|
|
|
O21 |
S[2,3]23 |
|
||
|
|
|
|
A |
|
−S |
|
|
||||||||||
exp(−iK |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Разветвлённый участок (рис. 26c) не является элементарным. Так как в этом случае
E ={1}, N ={{1,2,3},{3,4},{2,4}}, сетевая формула (167) примет вид
S[1] = S[1,2,3] S[3,4] S[2,4] |
(339) |
119
Раскроем операцию объединения при расчёте S[1,2,4] = S[1,2,3] S[3,4] . Здесь для формулы объединения (160) имеем: J ={1,2} , K ={3}, L ={4} . Тогда, следуя примеру (69), запи-
шем её в виде
|
[1,2,3]11 |
|
[1,2,3]12 |
S |
|
S |
|
S[1,2,4] = S[1,2,3]21 |
S[1,2,3]22 |
||
|
O41 |
|
O42 |
|
|
|
|
−S[1,2,3]33
exp(−iK 33 A33 )
14 |
|
|
[1,2,3]13 |
13 |
|
|
O |
|
S |
|
O |
|
× |
O24 |
|
+ S[1,2,3]23 |
O23 |
|
||
S[3,4]44 |
|
O43 |
S[3,4]43 |
|
||
|
|
|
|
|
|
(340) |
exp(−iK 33 A33 ) −1 |
S[1,2,3]31 |
S[1,2,3]32 |
O34 |
|
||
−S[3,4]33 |
|
|
O31 |
O32 |
S[3,4]34 |
|
|
|
|
||||
|
|
|
|
|
|
|
При раскрытии S[1] = S[1,2,4] S[2,4] |
по формуле (160) J ={1}, |
K ={2,4}, L = , следова- |
||||||||||||||
тельно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
[1] |
= S |
[1,2,4]11 |
|
[1,2,4]1{2,4} |
1{2,4} |
|
× |
|
|
|
|
|
|
||
|
|
+ S |
|
O |
|
|
|
|
|
|
|
|
||||
|
|
|
−S[1,2,4]{2,4}{2,4} |
|
exp(−iK{2,4}{2,4} A{2,4}{2,4} ) −1 |
S[1,2,4]{2,4}1 |
(341) |
|||||||||
|
|
× |
|
|
{2,4}{2,4} {2,4}{2,4} |
) |
|
|
[2,4]{2,4}{2,4} |
|
|
O |
{2,4}1 |
|
||
|
|
|
|
|
|
A |
|
|
−S |
|
|
|
|
|
||
|
|
exp(−iK |
|
|
|
|
|
|
|
|||||||
В выражении (341) объекты с индексами {2,4} также можно раскрыть с помощью приме-
ра (69). Здесь это не сделано в связи с громоздкостью конечного выражения.
Одномерная сеть
Одной из разновидностей квантовых сетей является одномерная сеть. Она представляет собой последовательность финитных потенциалов и состоит из замкнутых и/или последовательных участков (рис. 26a и рис. 26b). Запишем их S-матрицы (336) и (338), используя для иллюстрации идентификаторы на основе нумерации узлов (индексы в угловых скобках), приемлемые для сетей малых размеров. Для замкнутых и последовательных участков (рис. 26a и рис. 26b) введём обозначения:
S 3 := S[1], |
S 1 |
:= S[1,2], |
S 2 |
:= S[2] |
(342) |
S 3 := S[1,3], |
S 1 |
:= S[1,2], |
S 2 |
:= S[2,3] |
(343) |
соответственно. В обоих случаях сократим обозначения: κ2 = |
ε =:κ , a2 =: a . Поскольку |
||||
величины в (342) и (343) являются |
числами, они коммутируют между собой. Поэтому |
|||
формулы (336) и (338) с учётом (158) |
упрощаются: |
|
||
S 3 = S 1 11 + |
S 1 12 S 2 22 S 1 21ei2κa |
(344) |
||
1− S 1 22 S 2 22ei2κa |
||||
|
|
|
||
120
|
1 11 |
|
|
S 1 12S 2 22S 1 21ei2κa |
|
|
|
|
S 1 12S 2 23eiκa |
|
|
|
|
|
|||||||||||||||||||
S |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
− S |
1 22 |
S |
2 22 |
e |
i2κa |
|
1− S |
1 22 |
S |
2 22 |
e |
i2κa |
|
|
(345) |
|||||||||||||||
S 3 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
S 2 32S 1 21eiκa |
|
|
S |
2 33 |
+ |
|
S 2 32S 1 22S 2 23ei2κa |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1− S |
1 22 |
S |
2 22 |
e |
i2κa |
|
|
|
1 |
− S |
1 22 |
S |
2 22 |
e |
i2κa |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
соответственно. Для «безрукавной» сети (165) с учётом специфики обозначений выражение (345) совпадает с выражением, полученным ранее [35, с. 49].
Таким образом, сетевая формула (167) показала свою эффективность при расчёте S- матриц участков квантовых сетей в примерах, представленных на рисунке 26.
Приложение E. Гексагональная квантовая сеть в одноканальном приближении
Актуальность
К числу перспективнейших материалов для современной наноэлектроники относятся аллотропные модификации углерода: графен, фуллерен, нанотрубки. Это связано с их уникальными электрическими свойствами, обусловленными спецификой строения кристаллической решётки. Её численное моделирование позволяет предсказывать характеристики углеродных наноструктур, что актуально для техники. Функциональную модель кристаллической решётки можно построить на основе квантовой сети. В этом случае достигается высокая скорость и гибкость расчётов, способные обеспечить данному подходу широкую область применения.
Структура сети
При моделировании кристаллической решётки аллотропных модификаций углерода представляет интерес задача рассеяния электрона в гексагональной квантовой сети (рис. 27). На рисунке сеть имеет шесть внутренних симметричных Y-узлов и шесть внешних узлов. Её структура запишется
N ={{1,7,8},{2,8,9},{3,9,10},{4,10,11},{5,11,12},{6,12,7}} |
(346) |
Все рукава сети одинаковы:
{K kk = K ll , Akk = All }k ,l I E |
(347) |
где I ={7,8,9,10,11,12} и E ={1,2,3,4,5,6}.
