Вопросы для самоконтроля

1. Назовите степенные средние.

2. Назовите структурные средние.

3. Как определить среднее арифметическое?

4. Что называется степенью свободы?

5. Как вычислить дисперсию и среднее квадратическое?

6. Как определить ошибку среднего арифметического?

7. Назовите основные параметры математической статистики?

8. Как определить необходимое число наблюдений?

 Рекомендуемая литература [1, 4, 10, 11, 22].

4. Распределение случайных величин

4.1. Нормальное распределение

Пусть из генеральной совокупности извлечена выборка, причем х₁ наблюдалась n₁ раз, х₂ – n₂, х₃ – n₃ раз, а  n_i = n – объем выборки. Наблюдаемые значения х_i – варианты, а последовательное написание их в возрастающем порядке – вариационный ряд. Числа наблюдений n_i называются частотами, а их отношение к объёму выборки – относительными частотами.

Перечень вариант и соответствующих им частот, или относительных частот называется статистическим распределением выборки или зако­ном распределения случайной величины. Собственно законом распре­деления случайной величины называется всякое соотношение, устанав­ливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Простейшей формой задания этого закона является таблица, в ко­торой перечислены значения случайной величины и соответствующие им частоты, относительные частоты или вероятности. Такую таблицу называют рядом распределения (табл. 4.1).

Таблица 4.1

Ряд распределения

хi	х1	х2	х3	……….	хn
pi	p1	p1	p1	……….	pn

Для наглядности строят различные графики распределения. В случае геометрического представления ряда распределения дискретных слу­чайных величин получаем многоугольник распределения (рис. 4.1) или полигон частот.

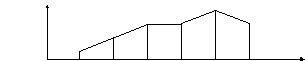
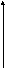
х₁ х₂ х₃ х₄ х₅ х₆

Рис. 4.1. Многоугольник распределения

Для его построения на оси абсцисс откладывают варианты х_i, а на оси ординат – соответствующие им относительные частоты w_i, Точки (х_i, w_i,) соединяют отрезками прямых и получают полигон частот. Много­угольники распределения могут быть различными по форме, что еще раз подчеркивает случайность явления (рис. 4.2).

а

б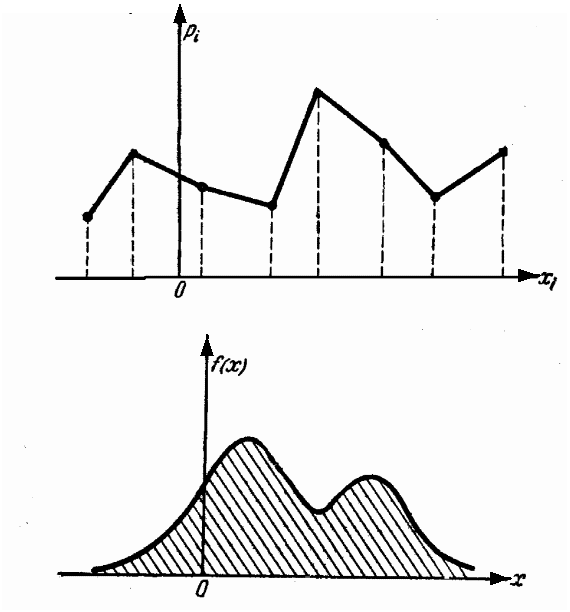

Рис. 4.2. Многоугольник дискретного распределения (а); кривая непрерывного распределения (б)

Если многоугольник распределения (кривая распределения) имеет более одного максимума, распределение называется «полимодаль­ным». Иногда встречаются распределения, обладающие посередине не максимумом, а минимумом. Такие распределения называют «антимо­дальными» (рис. 4.3).

Рис. 4.3. Антимодальное распределение (а и б см. пояснения к рис. 4.2)

Два последних термина см. в разд. 3, где кроме важнейших из харак­теристик положения – математического ожидания, упоминались и дру­гие, в частности мода (рис. 4.4) и медиана (рис. 4.5).

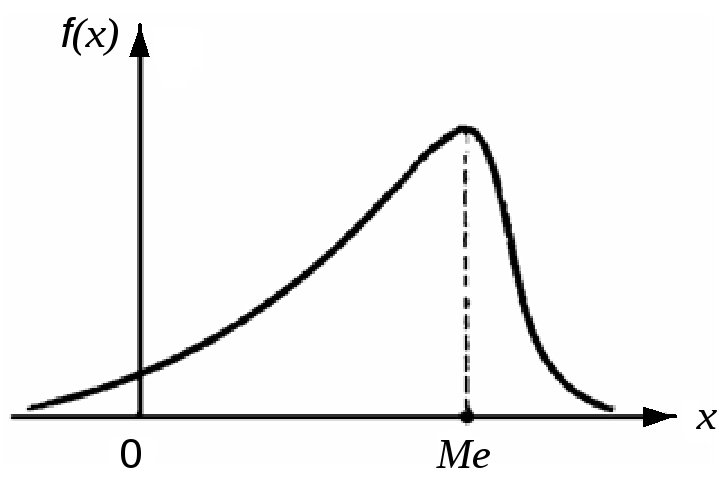
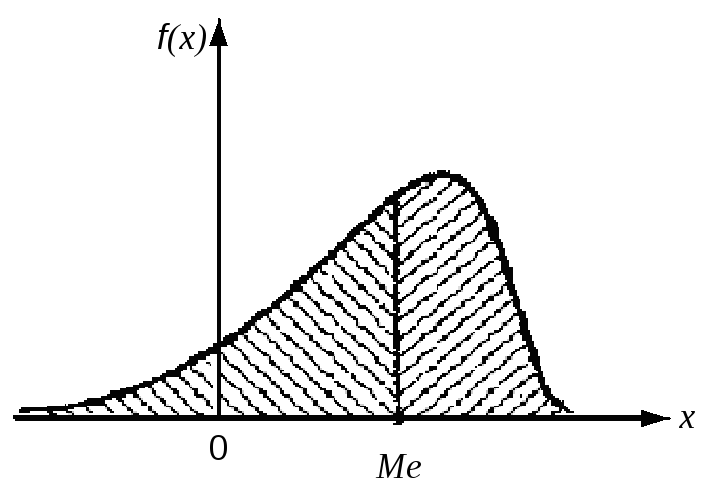
Рис. 4.4. Мода случайной величины Рис. 4.5. Медиана распределения

Модой случайной величины называется ее наиболее вероятное зна­чение. В общем случае мода и математическое ожидание случайной ве­личины не совпадают. В частном случае, когда распределение является симметричным и модальным (т. е. имеет моду) и существует математи­ческое ожидание, то оно совпадает с модой и центром симметрии рас­пределения.

Часто применяемой еще одной характеристикой положения – медиа­ной (рис. 4.5), пользуются обычно только для непрерывных случайных величин, хотя формально ее можно определить и для дискретной величины.

Медианой случайной величины х называется такое число Me, для которого

Р(Х < Ме) = Р(Х > Ме),

т. е. одинаково вероятно, окажется ли случайная величина меньше или больше Me. Геометрическая медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.

В случае симметричного модального распределения медиана совпа­дает с математическим ожиданием и модой.

Распределение случайных величин является математической моде­лью вероятностного процесса, отличающегося тем, что элементарные исходы могут проявляться в самой разнообразной форме по численному значению и частоте.

Математической модели может быть подобрана физическая модель, а для нее в свою очередь – математическая модель распределения.

Итак, ряд распределения является законом распределения для дис­кретной (непрерывной) случайной величины. Простейшим примером дискретного распределения является ситуация с п равновероятностны­ми исходами. Физической моделью такого распределения являются ис­ходы бросания монеты, кубика и т. д.

Но для непрерывной величины ряда не существует. В то же время различные области возможных значений случайной непрерывной вели­чины не являются одинаково вероятными, поэтому и для непрерывной величины существует также распределение вероятностей.

В случае непрерывного признака для геометрического представле­ния целесообразно строить гистограмму (рис. 4.6).

Рис. 4.6. Гистограмма частот

Для этого весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частных интервалов длиной х, находят для каждого частного интервала п_i – сумму частот вари­ант, попавших в i-й интервал. Гистограммой частот называют ступенча­тую фигуру, состоящую из прямоугольников, основаниями которых слу­жат частные интервалы длиной х, а высоты равны (плотность частоты). Площадь такого прямоугольника равна , а сумма площадей всех прямоугольников (площадь гистограммы) .В слу­чае использования относительных частот или вероятностей площадь гистограммы будет равна единице.

Вероятность непрерывного события х есть функция от х. Эта функ­ция называется функцией распределения случайной величины х и обо­значается F(x). Функцию распределения называют также интегральной функцией распределения или интегральным законом распределения величин

. (4.1)

Функция распределения непрерывной случайной величины F(х), оп­ределяющая вероятность того, что случайная величина х принимает ка­кое-нибудь значение в пределах интервала а, b, определится как

.

Интегральная кривая этой функции (рис. 4.7) монотонно возрастает от нуля (при х = – ) до единицы (при х = ). Обратная функция дает значение х, соответствующее заданной вероятности не­превышения Р(х). Эти значения называют квантилями вероятности Р(х).

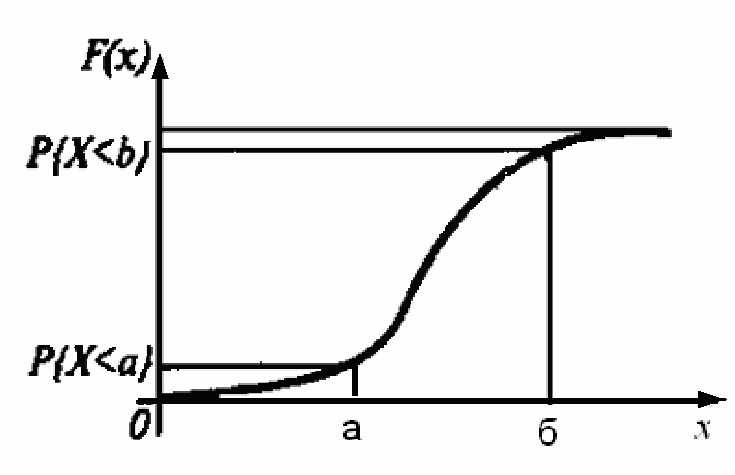
Рис. 4.7. Интегральная функция распределения

Функция является производной функции распределения F(х) и характеризует плотность, с которой распределяются значения случай­ной величины. Эта функция называется плотностью распределения или плотностью вероятности. Иногда её называют функцией распределения, или дифференциальным законом распределения случайной величины.

Плотность распределения является пределом отношения вероятно­сти события, состоящего в том, что непрерывная случайная величина принимает значения, лежащие в заданном малом интервале, к длине интервала, когда эта длина стремится к нулю.

Кривую, изображающую плотность распределения случайной вели­чины на графике дифференциальной функции распределения (рис. 4.8), называют кривой распределения. Кривые распределения могут иметь чрезвычайно разнообразную форму.

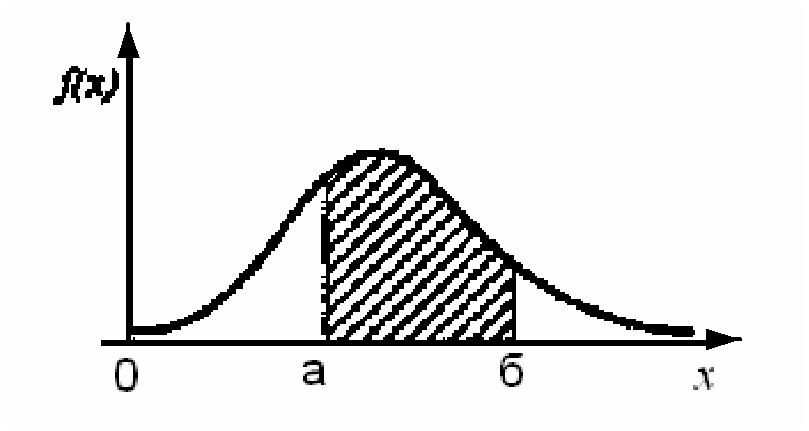
Рис. 4.8. Плотность распределения