4.5. Обработка результатов измерений

В результате наблюдений, проведения экспериментов, испытаний у исследователя накапливается ряд характеристик случайной величины х, закон распределения которой точно неизвестен и его следует опре­делить.

А. Дискретное распределение.

Если мы имеем дело с дискретной случайной величиной X, которая в ходе испытаний приняла п₁ раз значение х₁, п₂ раз значение х₂, n_k раз значение х_k, а n_i = п, то обработка результатов ведётся в сле­дующем порядке.

Пусть имеются основания предположить, что изучаемая величина X распределена по некоторому определённому закону. Чтобы проверить, согласуется ли это предположение с данными наблюдений, вычисляют частоты наблюдаемых значений, т. е. находят теоретическую частоту каждого из наблюдаемых значений в предположении, что величина X распределена по предполагаемому закону.

Выравнивающими (теоретическими) частотами в отличие от факти­чески наблюдаемых эмпирических частот называют частоты, найден­ные теоретически (вычислением). Выравнивающие частоты находят из равенства

= nР_i, (4.27)

где n – число испытаний; Р_i–вероятность наблюдаемого значения х, вычисленного при допущении, что х имеет предполагаемое распреде­ление.

Итак, выравнивающая частота наблюдаемого значения х_i дискретно­го распределения равна произведению числа испытаний на вероятность этого наблюдаемого значения.

Пример 4.1. В результате эксперимента, состоящего из п = 520 ис­пытаний, в каждом из которых регистрировалось число х_i появлений не­которого события, получено следующее эмпирическое распределение:

наблюдаемые значения… х_i 0 1 2 3 4 5 6 7

эмпирическая частота... n_i 120 167 130 69 27 5 1 1

Найти выравнивающие частоты в предположении, что случайная величина X (генеральная совокупность) распределена по закону Пуас­сона.

Решение: известно, что параметр , которым определяется распре­деление Пуассона, равен математическому ожиданию этого распреде­ления. Поскольку в качестве оценки математического ожидания прини­мают выборочную среднюю, то и в качестве оценки , можно принять выборочную среднюю . Легко найти по условию, что выборочная сред­няя равна 1,5, следовательно, можно принять = 1,5.

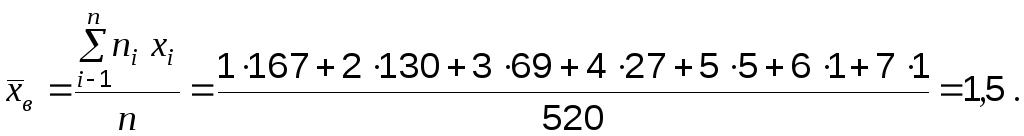
Таким образом, формула Пуассона

(4.28)

принимает вид

. (4.29)

Пользуясь этой формулой, найдем вероятность прик = 0,1,2,3,4,5,6,7 (для простоты записи индекс 520 далее опустим): Р(0) = 0,22313, Р(1) = 0,33469, Р(2) = 0,251021, Р(3) = 0,125511, Р(4) =0,047066, Р(5) = 0,014120, Р(6) = 0,003530, Р(7) = 0,000755.

Найдем выравнивающие частоты (результаты умножения округлены до единицы): = n Р(0) = 520 · 0,22318 = 116;

= n Р(1) = 520 · 0,33469 = 174.

Аналогично найдем и остальные выравнивающие частоты. В итоге получим:

эмпирические частоты ........ 120 167 130 69 27 5 1 1

выравнивающие частоты.. .. 116 174 131 65 25 7 2 0.

Сравнительно небольшое расхождение эмпирических и теоретиче­ских (выравнивающих) частот подтверждает предположение, что рас­сматриваемое распределение подчиняется закону Пуассона.

Заметим, что если подсчитать выборочную дисперсию по данному распределению, то окажется, что она равна выборочной средней, т. е. 1,5. Это служит ещё одним подтверждением сделанного предполо­жения, поскольку для распределения Пуассона

. (4.30)

Конечно сравнение эмпирических и теоретических частот «на глаз» дело сложное и требует определенного навыка. Чтобы сделать это обоснованно, надо использовать, например, критерий Пирсона. Провер­ка гипотезы о распределении случайной величины по закону Пуассона изложена в [9, 10].

Б. Непрерывное распределение.

В случае непрерывного распределения вероятности отдельных воз­можных значений равны нулю. Поэтому весь диапазон возможных зна­чений делят на интервалы или разряды и подсчитывают количество значений m_i, величины x_i, приходящихся на i-й разряд. Это число делят на общее число наблюдений n и находят частоту разряда или статисти­ческую вероятность:

. (4.31)

Сумма частот всех разрядов равна единице:

. (4.32)

Составляют таблицу, в которой приведены разряды в порядке их расположения вдоль оси абсцисс и соответствующие им частоты. Эту таблицу называют статистическим, или вариационным рядом. Число разрядов В.Г. Зазимко [11] рекомендует принимать в пределах от 7 до 15; В.А. Вознесенский [5] считает, что их количество не должно превышать 20–25, так как при увеличении числа разрядов резко возрастает трудоем­кость статистических расчетов, а точность результатов не изменяется.

Длину интервалов h_x можно определить из удобства расчетов и об­щего диапазона значений х, но можно вычислить по выражению

h_x =(4.33)

где х_п и х₁ – крайние числа вариационного ряда соответственно Х_max и Х_min; n – число наблюдений.

Для построения гистограммы (графического представления стати­стического ряда) по оси абсцисс откладываем разряды, а по оси орди­нат – число наблюдений m_i, соответствующее частоте Р_i.. Получим сту­пенчатый график, состоящий из прямоугольников разной величины, вна­чале увеличивающихся, а затем уменьшающихся по высоте. Если со­единить точки середины верхней стороны каждого прямоугольника ли­нией, то получится эмпирическая кривая плотности распределения ве­личины х. Площадь, ограниченная этой кривой, равна единице.

После построения гистограммы подбирают теоретическую кривую распределения, более точно описывающую статистический материал. Для этого нужно определить теоретические выравнивающие частоты, т. е. решить задачу выравнивания или сглаживания статистических рядов.

Если есть основания предположить, что случайная величина X (ге­неральная совокупность) распределена нормально, то выравнивающие частоты могут быть найдены по формуле

(4.34)

где п – число испытаний (объем выборки); h – длина частичного интервала; _в – выборочное среднее квадратическое отклонение;

(х_i – середина i-го частичного интервала);

. (4.35)

Если величина х подчиняется нормальному закону, то задачу вы­равнивания можно перевести в задачу о рациональном выборе пара­метров х и _x.

Пример 4.2. Сравним кривые эмпирического и теоретического рас­пределения плотности вероятности прочностных характеристик бетона. Результаты испытаний 180 образцов бетона на прочность сведены в статистический ряд (табл. 4.2), при этом частота разряда, или статисти­ческая вероятность p_i определена по формуле (4.31). Статистический ряд для рассматриваемого примера представим графически в виде гистограммы (см. рис. 4.6).

Таблица 4.2

Статистический ряд

Параметры	Значения параметров по интервалам прочности бетона, МПа									Сум­ма зна­чений ряда
	12,1–14,0	14,1–16,0	16,1–18,0	18,1–20,0	20,0–22,0	22,1–24,0	24,1–26,0	26,1–28,0	28,1–30,0
Число зна-
чений проч­ности в области ин-	3	3	30	40	41	31	16	5	1	N=180
тервала mi
Частота разряда или ста­тистическая вероятность Pi
	0,017	0,072	0,167	0,222	0,228	0,172	0,089	0,028	0,005	1

Для построения теоретической кривой или кривой нормального распределения введем нормированное отклонение и воспользуемся следующей формулой нормального нормированного распределения

, (4.36)

а так же формулами для определения средней арифметической х₀

(4.37)

и среднего квадратического отклонения

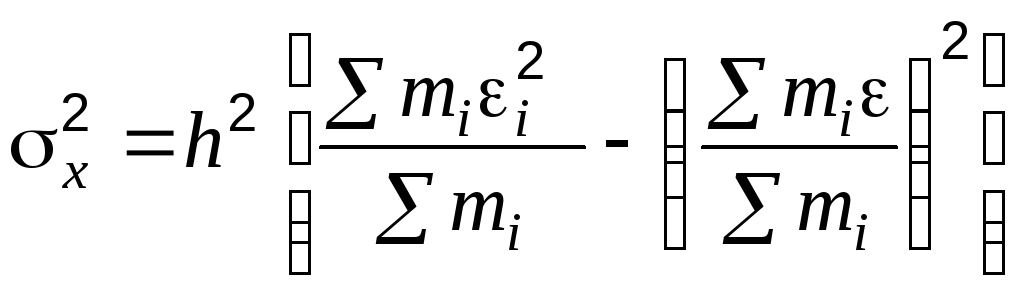, (4.38)

где h – размер интервалов, на которые разбита совокупность определе­ний прочности; – общее число определений прочности; – от­носительная величина, удобная для вычислений;

 , (4.39)

С – начало условного отсчета, соответствующее примерно середине об­щего интервала определения прочности (для данного случая С = 21). Ре­зультаты выполненных расчетов сведём в табл. 4.3, по которой удобно делать сравнение кривых эмпирического и теоретического распределения.

Используя формулы (4.37), (4.38), определим величины х₀ и _х

;

Теоретическое число значений прочности определено по формуле

.

Сравнение эмпирических т_i и теоретических величин показыва­ет, что они близки между собой. Это подтверждается и на рис. 4.21, где экспериментальная кривая распределения прочности бетона практиче­ски повторяет теоретическую.

Однако определение близости кривых по графику может быть не­достаточно точным. Разные исследователи по-разному могут оценивать расхождение между ними.

В статистике разработан ряд объективных оценок, называемых кри­териями согласия. Воспользуемся уже названным ранее критерием Пирсона, основанным на ^2-распределении

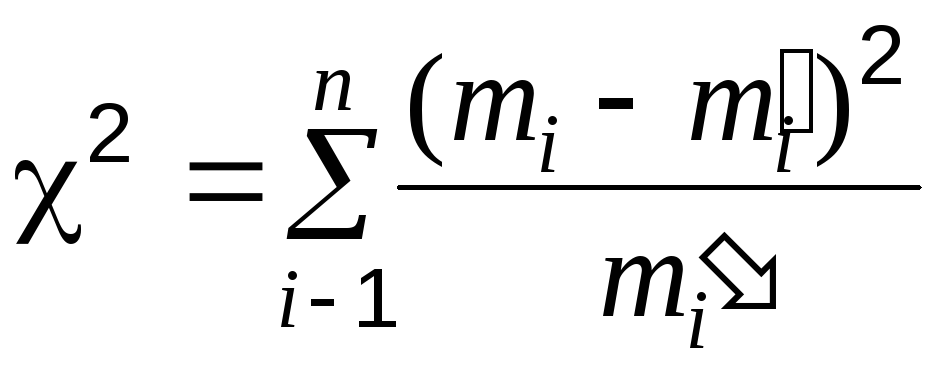, (4.40)

где т_i и – соответственно эмпирические и теоретические частоты распределения; п – число интервалов (разрядов).

Критерий ^2 является наиболее состоятельным при большом числе наблюдений. Его состоятельность заключается в том, что он почти всегда отвергает неверную гипотезу, т. е. обеспечивает минимальную ошибку в принятии неверной гипотезы по сравнению с другими критериями.

Таблица 4.3

Результаты расчетов

Среднее значение прочности в интер-вале хi, МПа	Число значений прочности в интервале mi (эмпир)	 =	mi	mi2	xi – x0	u =	(u)	Число значений прочности в интер-вале (теорет.)	Округленное значение
13 15 17 19 21 23 25 27 29	3 13 30 40 41 31 16 5 1	–4 –3 –2 –1 0 1 2 3 4	–12 –39 –60 –40 0 31 32 15 4	48 117 120 40 0 31 64 45 16	–7,2 –5,2 –3,2 –1,2 0,8 2,8 4,8 6,8 8,8	–2,25 –1,63 –1,00 –0,38 0,25 0,88 1,50 2,13 2,75	0,031 0,106 0,242 0,371 0,387 0,271 0,130 0,041 0,009	3,57 11,9 27,2 41,7 43,5 30,5 14,6 5,7 1	3 12 27 42 44 30 15 6 1
–	180	–	 mi= = –69	 mi= =481	–	–	–	–	= 180

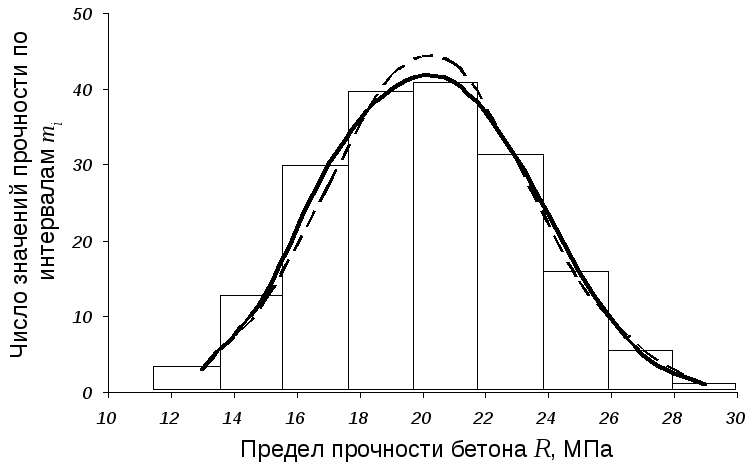
Рис. 4.21. Экспериментальная и теоретическая

кривые распределения плотности и вероятности

Критерий ^2 применим и тогда, когда теоретические значения параметров функции распределения неизвестны.

.

Пользуясь табл. 3 прил. 2 в зависимости от числа степеней свободы и уровня значимости 0,05 находим ^2. Если ^2_кр  ^2_набл,то расхождение между эмпирической и теоретической кривыми распределения можно признать случайным и незначимым.

Число степеней свободы f = к – r – 1 (к – число разрядов, r – число параметров для нормального распределения 2: х₀ и _х)

f = 9 – 2 – 1 = 6.

По табл. 3 прил. 2 находим, что при уровне значимости 0,05 и f = 6, ^2_кр = 12,6, т. е. ^2_кр  ^2_набл.

Следовательно, данные наблюдений согласуются с гипотезой о нор­мальном распределении генеральной совокупности.

При отсутствии таблиц ^2 можно воспользоваться формулой Рома­новского. Если выполняется соотношение

, (4.41)

то эмпирическое распределение согласуется с нормальным:

.

Этот критерий также подтверждает вывод о согласовании с нормаль­ным эмпирического распределения результатов испытаний бетона.

Наконец, оценку степени близости наблюдаемого распределения к нормальному можно оценить с помощью -критерия (по теореме А.Н. Колмогорова, табл. 4.4). Критерий  определяют по выражениям:

, (4.42)

где D_mах – максимальное отклонение теоретической интегральной функции типа Ф(и) от эмпирической функции; N – накопленные эмпи­рические частоты, которые определяют последовательным сложением частот; – накопленные теоретические частоты; п – число измерений.

При известном значении  по табл. 2 прил. 2 находят вероятность P(). Исходя из практического опыта можно считать расхождение ме­жду эмпирическим и теоретическим нормальными распределениями не­значительным уже при P()  0,6.

Только при значении P() < 0,05 расхождение признают неслучай­ным, т. е. распределение не соответствует нормальному закону.

Таблица 4.4

Определение максимальной разности накопленных частот

Границы интервалов прочно­сти бетона, МПа	Частота (число зна­чений прочности) в каждом интервале		Накопленная частота		Разность накопленных частот
	эмпирическая т	теорети­ческая	эмпири­ческая N	теорети­ческая N
12,1–14,0	3	2,7	3	2,7	0,3
14,1–16,0	13	11,9	16	14,6	1,4
16,1–18,0	30	27,2	46	41,8	4,2(mах)
18,1–20,0	40	41,7	86	83,5	2,5
20,1–22.0	41	43,5	127	127,0	0,0
22,1–24,0	31	30,5	158	157,5	0,5
24,1–26,0	16	14,6	174	172,1	1,9
26,1–28,0	5	5,7	179	177,8	1,2
28,1–30,0	1	1	180	178,8	1,2

По формуле (4.42)

,

.

Ближайшее табличное значение  = 0,3 (табл. 2 прил. 2), а вероят­ность P() = 1. Это значит, что расхождение между эмпирическим и тео­ретическим распределениями практически отсутствует.