4.3. Критерий близости распределения к нормальному

Иногда для оперативной оценки характера распределения результатов наблюдений можно обойтись без построения кривой и необходимых при этом расчетов. Отклонение от нормального распределения может быть случайным и неслучайным. Если оно неслучайно, то возникает необходимость изменения методики определения. Если отклонение случайно, то необходимо определить степень отклонения от нормального распределения или выяснить, какому другому оно подчиняется (t- илиF-распределению).

В статистике разработан ряд критериев для оценки степени близости наблюдаемого распределения к нормальному (, ^2и др.).

Оценка с помощью -критерия производится на основании теоремы академика А.И. Колмогорова о распределении максимума отклонений теоретической интегральной функции распределения от соответствующей эмпирической функции

; (4.19)

, (4.20)

где – максимальное отклонение теоретической интегральной функции типаот эмпирической функции;– накопленные эмпирические частоты, которые определяют последовательным сложением частот;– накопленные теоретические частоты;n– число измерений.

При установленном в табл. 2 прил. 2 находят вероятность. Из практического опыта можно считать расхождение между эмпирическим и теоретическим нормальными распределениями незначительным уже при0,6. Лишь при0,05 расхождение в распределениях признают неслучайным, а это значит, что распределение не соответствует нормальному.

Пригодность нормального распределения может быть проверена по результатам асимметрии и эксцесса. Если характеристики асимметрии и эксцессаЕблизки к 3, то нормальное распределение пригодно для описания явления

; (4.21)

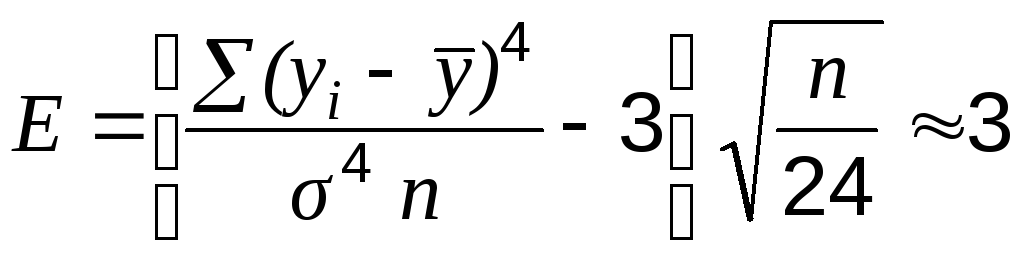. (4.22)

Пригодность нормального распределения может быть проверена с использованием чисел Вестергарда: если в область входит 25 %,– 50 %,– 75 % и– 99,8 % всей совокупности, применение Гауссова распределения оправдано.

4.4. Закон распределения при малом числе испытаний

В случае малых выборок, с чем чаще встречаются на практике, вероятность появления больших отклонений значительно уменьшается. Даже в случае 20 наблюдений вероятность появления отклонения, превышающего 2 , равна 5 %. Поэтому классическая теория, основанная на нормальном распределении, при малых выборках неприменима. Обработки данных в этом случае принимают другие законы, разрабатываемые микростатистикой.

Распределение Стьюдента (t-распределение).Величинаимеет распределение, кривые плотности вероятности которого напоминают кривые нормального распределения, значительно медленнее сближающиеся с осью абсцисс. Распределениезависит только от числа степеней свободы, по которому определяют выборочную дисперсию. Значениеприведено в табл. 4 прил. 2.

Число степеней свободы принимается каждый раз равнымn – 1.

Как уже отмечалось, при n=20 -распределение ещё хорошо аппроксимируется нормальным распределением. Большая разница в величине возникает при 10.

Если – вероятность того, что случайная величина находится за пределами интервала , то вероятность попадания в этот интервал определяется выражением

. (4.23)