
BiometriaKnuga
.pdfРозділ 3.8 ЕкологіяОсновні особливості розподілу імовірностей |
|
151 |
|
||
|
|
|
У останньому прикладі, коли n = 10, ця крива буде мати вигляд, що представлений на рис. 9. Слід звернути увагу на те, що при будь-якому степеню біному (n), число коефіцієнтів буде дорівнювати: n + 1, так, при n = 2 воно равно 3, при 6 − 7, при 10 − 11, а сума біномінальних коефіцієнтів равна 2n (при N = 2 це буде 22, при N = 6 − це 62, при N = 10 − це 102, в наведених прикладах − 4, 8, 64, 1024.
Наведені вище приклади відносяться до ситуацій, коли p i q мають однакові значення. Але коли p i q не рівні (p ≠ q), то розподіл буде асиметричним. Причому асиметричність буде в більшому ступеню, чим менше значення (n). Якщо кількість випробувань (n) досягає 30 і більше, розподіл приймає симетричний характер, і тоді діє наступна закономірність.
Якщо подія (А) зустрічається в (n) випробуваннях, то протилежна подія
(A) буде зустрічатись (n − m) разів, і імовірність будь-якого результату буде дорівнювати pmхqn-m, тому імовірність Рn(m) події (А) з’явиться (m) разів в (n) незалежних випробуваннях, що апроксимуються формулою Якоба Бернуллі:
Висновок. Закон біномінального розподілу описується двочленною формулою бінома Ньютона і аналогічною формулою Бернуллі.
Біномінальний закон діє в біологічних сукупностях: за цим законом розподіляються альтернативні ознаки.
У випадках значної кількості випробувань застосування формули Бернуллі стає важким, і тоді використовується формула Лапласа.
Розділ 3.8 ЕкологіяОсновні особливості розподілу імовірностей |
|
151 |
|
||
|
|
|
8.3. Нормальний розподіл
Нормальний розподіл нерозривно повўязаний з особливістю функції. Нагадаємо, що функція є значення однієї змінної ознаки щодо другої також змінної ознаки, яка умовно вважається аргументом. Тобто, якщо відповідному значенню незалежної змінної величини Х, яка зветься аргумент,

152 |
|
Біометрія |
|
відповідає одне значення другої змінної величини Y, яка зветься функція, то кажуть "Y є функція від Х":
у = f (x).
Приклад: у = 2х; у = 0,1х.
Для того, щоб знайти закон розподілу змінної випадкової величини, необхідно знайти функціональну залежність між числовими значеннями, які вона може приймати і імовірностями цих значень.
Для випадків альтернативного варіювання ця залежність визначається наведеною вище формулою:
|
|
1 |
− |
(mnp)2 |
|
|
|
|
|
||
P (m) = |
|
|
e 2npq . |
||
|
|
||||
n |
2πnpq |
|
|
|
|
|
|
|
|
|
|
Але для безперервної випадкової величини визначити за таким принципом імовірність її значення неможливо. Тому враховуються лише ті значення, які випадкова безперервна величина може прийняти із тією або іншою імовірністю в певному інтервалі: від − до, наприклад від (х) до (х + dx) (тут dx − ширина інтервалу).
Математики Муавр (1733), Лаплас (1780) і Гаусс (1809), незалежно один від одного, довели теорему про те, що імовірність (Р) будь-якого значення (х) безперервної випадкової величини, що знаходиться в інтервалі від (х) до (dx), описується наступною формулою:
|
|
1 |
|
− |
(x−M )2 |
||
|
|
|
|
|
|||
P(x) = |
|
|
e 2σ2 dx, |
||||
|
|
|
|
||||
σ |
|
2π |
|||||
|
|
|
|
|
|
||
де π − 3,1415...; е − 2,7183...; σ − стандартне або середньоквадратичне відхилення, яке
характеризує розмір варіації випадкової величини; М − середня величина або математичне очікування.
Формула Гауса–Лапласа описує закон нормального розподілу випадкової величини.
Розділ 3.8 ЕкологіяОсновні особливості розподілу імовірностей |
|
153 |
||||||
|
||||||||
|
|
|
||||||
Значення (x – M) / σ є нормоване відхилення, тобто − t. Тоді |
|
|||||||
1 |
|
− |
1 |
t2 |
|
|||
|
|
|
||||||
f (t) = |
|
|
|
e 2 . |
|
|||
|
|
|
|
|||||
2π |
|
|||||||
|
|
|
|
|
|
|
|
|
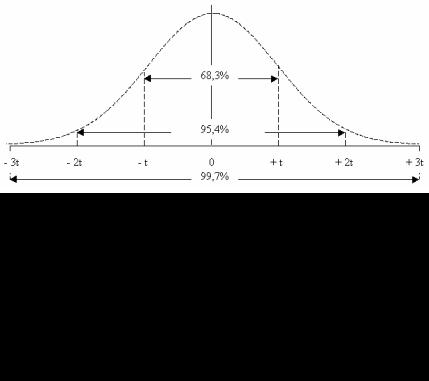
Нам вже відомо, що t − випадкова величина, для якої середньоквадратичне відхилення дорівнює 1, а математичне очікування = 0. Отже, чим більше значення окремої ознаки відхиляється від 0, тим менша буде кількість таких ознак. Крива, що описується цим рівнянням зветься кривою нормального розподілу. Особливістю нормального розподілу є те, що від 0 в межах від − t до + t розміщується 68,3 % від числа всіх членів сукупності, в межах − 2t до +2t − 95,4, а в межах від −3t до +3t − 99,7 % всіх членів сукупності (рис. 10).
Рис. 10. Крива нормального розподілу:
t − нормоване відхилення; P −імовірність знаходження середнього значення в межах відповідного нормованого відхилення
P1{–t < x – x < +t}=0,683, P2{–2t < x – x < +2t}=0,954, P3{–3t < x – x < +3t}=0,997
Часто для полегшення розрахунків (усувається необхідність обчислення t) замість t в апроксимації розподілу вживають значення σ (середнє квадратичне відхилення). Тоді графічний вираз кривої нормального розподілу буде таким, як на рис. 11.

154 |
|
Біометрія |
|
Межі, в яких з тією чи іншою імовірністю знаходиться параметр генеральної сукупності, що вивчається, звуться довірчими, а інтервал, що знаходиться в цих межах, зветься довірчим інтервалом.
Отже, довірчий інтервал в загальній формі можна визначити як
−t ≤ x − x ≤ +t,
σ
де t − нормоване відхилення, яке визначається межою довірчої імовірності за критерієм Стьюдента.
У перетвореному вигляді наведена залежність може бути представлена
як
x − tσ ≤ x ≤ x + tσ.
Якщо візьмемо довірчу імовірність Р = 0,95, який відповідає t = 1,96, невідомий генеральний параметр x в нормально розподіленій сукупності
знаходиться в інтервалі
x−1,96σ ≤ x ≤ x +1,96σ.
На рис. 11 графічно представлені довірчі межі, що відповідають трьом
Рис. 11. Довірчі інтервали при довірчій імовірності: Р1 = 0,95; Р2 = 0,99; Р3 = 0,999
Розділ 3.8 ЕкологіяОсновні особливості розподілу імовірностей |
|
155 |
|
||
|
|
|
рівням довірчої імовірності: Р = 0,95; 0,99; 0,999.
В біології нормальний розподіл ознак є найбільш поширеним. Він застосовується для вивчення екологічних (біотичних і абіотичних), антропогенних, кліматичних факторів і ситуацій на відповідний біологічний об'єкт, представлений сукупністю індивідуумів, ознак, явищ. Зміна особливостей нормального розподілу дає можливість оцінювати вплив даного фактору на структуру генеральної сукупності в межах ознаки, що вивчається. Порівняння нормального розподілу відповідних ознак різних генеральних сукупностей може дати оригінальне рішення прикладного значення.
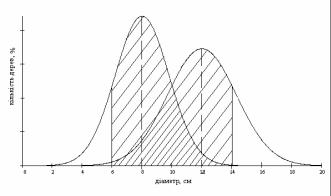
Наприклад. Співставлення двох кліматипів сосни звичайної показало, що інорайонний кліматип (К1) в порівнянні з місцевим кліматипом (К2) мають менші середні діаметри і середні висоти. Але розподіл діаметрів і висот дерев цих кліматипів засвідчив, що частини дерев інорайонного кліматипу мають більші висоти і діаметри, ніж половина дерев місцевого кліматипу. Це дало можливість теоретичного обгрунтування і практичного використання способу вирощування лісових культур із застосуванням сіянців − потомків дерев цих кліматипів. Спосіб був
Рис. 12. Особливості розподілу за висотою двох кліматипів сосни звичайної звичайної
156 |
|
Біометрія |
|
визнаний оригінальним і захищений авторським свідоцтвом [4] (рис. 12).
Слід відмітити, що ідеального в математичному відношенні нормального розподілу ознак в біометричних дослідженнях не зустрічається. Як відзначалось вище, завжди крива розподілу має відповідні відхилення від ідеальної за математичними розрахунками кривої, в якої в більшому або меншому степеню мають місце ексцеси і асиметрія. Вони завжди характеризують відповідні особливості об'єкту досліджень. Крім ексцесів і асиметрії, зустрічаються випадки, коли розподіл ознак описується на кривій, що має два або декілька вершин. Така особливість розподілу, як правило, є ознакою того, що у виборці присутні групи предметів, які біологічно дещо відрізняються за даною ознакою. Це буває, наприклад, коли в досліджуванй сукупності рослин одного виду присутні групи рослин різних добре визначених популяцій, біотипів або кліматипів.
156 |
|
Біометрія |
|
8.4. Розподіл Пуассона
Істотно змінюється характер нормального розподілу тоді, коли досліджується розподіл випадків, імовірність прояву яких дуже незначна і навіть наближується до 0. Тобто, коли n = p + q, але p ≠ q i p > q0,3−0,0. Це має місце, коли подія, що очікується, відбувається 0, 1, 2, 3 і т.д. разів на 1000 і більшу кількість випробувань. Тоді в n випробуваннях більша їх кількість буде мати зовсім незначні значення їх прояву. Отже, на відміну від нормального розподілу більша кількість випадків буде концентруватись не в зоні середнього значення показника частотності прояву ознаки (х), а на відрізку зменшення цього показника, тобто в межах від 0,0 до 0,5 частки значення (х). Причому, чим менша імовірність прояву очікуваних випадків, тим ближче до нульового значення (х) буде розміщуватись кількість випробувань (n) (рис. 13). Особливості такого розподілу були досліджені видатним математиком Пуассоном і представлені нижче.
Коли імовірності альтернатив істотньо не рівні, тобто p ≠ q, біномінальний розподіл стає асиметричним. Коли імовірність р очікуваної події дуже мала (соті і тисячні долі відсотку одиниці в порівнянні з протилежною імовірністю q події) розподіл його частоти в n незалежних

Розділ 3.8 ЕкологіяОсновні особливості розподілу імовірностей |
|
|
|
|
157 |
|
|
|
|
||
|
|
|
|||
Рис. 13. Розподіл Пуассона. |
|||||
Графік функцій |
|
|
|||
P (m) = |
am |
|
e−a |
||
|
|||||
|
n |
m! |
|
|
|
|
|
|
|
||
при а = 0,1 (1); 0,5 (2); 1,0 (3);
випробуваннях стає надто асиметричною.
В таких випадках частоти подій (m) описуються формулою Пуассона
(1837):
Pn (m) = am e−a , m!
де а − найбільш імовірна частота або математичне очікування рідкої події в серії незалежних випробувань (а np); m − частота очікуваної події в n незалежних випробуванях; n − кількість незалежних випробувань; е − 2,7183... − основа натуральних логарифмів; m! − факторіал частоти: 1 2 3 ... m.
або
am Pn (m) = m!ea .
Приклад: При а = 2 імовірність, що подія А не відбудеться

158 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Біометрія |
|
|
(m = 0), дорівнює: |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
20 |
1 |
|
|
|
|
1 |
|
|
|
||||||
|
Pn |
(0) = |
|
|
= |
|
|
|
|
= |
|
|
= 0,1353; |
|
||||
|
0!e2 |
|
|
2 |
7,389 |
|
||||||||||||
|
|
|
|
(2,7183) |
|
|
|
|
|
|||||||||
|
|
|
− імовірність одиничного здійснення події А (m = 1) буде |
|||||||||||||||
|
|
|
21 |
2 |
|
|
|
|
2 |
|
|
|
||||||
|
Pn |
(1) = |
|
|
= |
|
|
|
|
|
= |
|
|
= 0,2707; |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1!e2 |
(2,7183) |
2 |
|
|
7,389 |
|
|
|||||||
− імовірність 3-х випадків Pn(3)= 0,1805 і т.д.
Очікувані частоти m різних подій (представлені в додатку 6) вирахуванi за перетвореною формулою:
P'= xm e−x , m!
де Р’− теоретичні ординати кривої розподілу Пуассона, тобто очікуване число випадків рідкісних подій в кожному випробуванні: 0, 1, 2, 3,...; − середнє число фактично спостережуваних випадків.
Розподіл Пуассона є окремим випадком біномінального розподілу, його особливість − із збільшенням середньої а = np він наближається до кривої нормального розподілу (див. рис. 13).
