
- •1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- •2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
- •2.Однородные ду
- •5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
- •8.Линейная зависимость,независимость ф-ий. Определитель вронского.
- •9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
- •12Линейные однородные системы ду высших порядков с постоянными коэффициентами
- •13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
- •15 Устойчивость по Ляпунову
- •16 Устойчивость по первому приближению
- •19.Предел и непрерывность функций комплексной переменной.
- •22.Элеменарные функции комплексной переменной.
- •25.Теорема Коши и интегральная формула Коши.
- •26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
- •27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
- •28. Нули аналитических функций. И их классификация.
- •29. Ряд Лорана. Изолированные особые точки и их классификация.
- •32. Вычет аналитических функций.
- •35.Классификац.Ур. Матфизики.
- •42. Оригинал и изображение. Св-ва преобразования Лапласа: линейность, подобие.
- •44. Формулы обращения преобразования Лапласа.
- •45. Применение преобразования Лапласа: теоремы обращения.
- •46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
- •47. Применение преобразования Лапласа к решению физических задач.
- •48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
29. Ряд Лорана. Изолированные особые точки и их классификация.
Выражение
вида
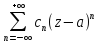 =
=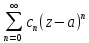 +
+ (1);
(1);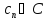 ;
;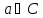 -
фиксирован.тчк- ряд Лорана. Область
сходим ряда(1)- общая часть областей
сходим.рядов, стоящих в правой части
рав-ва(1).
-
фиксирован.тчк- ряд Лорана. Область
сходим ряда(1)- общая часть областей
сходим.рядов, стоящих в правой части
рав-ва(1).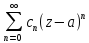 сход в некотором круге
сход в некотором круге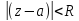 ;
;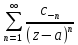 =
= =
=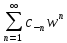 (*)-сход
в некотором круге
(*)-сход
в некотором круге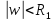 ,откуда
,откуда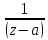 <
<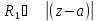 >
>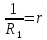 ,
след-но (*) сход в область
,
след-но (*) сход в область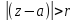 (
внешность круга радиусомr
с центром в тчк a).
Если 0<r<R,
то р.Лорана (1) схо в кольцевой обл r<
(
внешность круга радиусомr
с центром в тчк a).
Если 0<r<R,
то р.Лорана (1) схо в кольцевой обл r<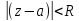 ;
еслиr
;
еслиr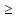 R,
то р.Лорана (1) не сход ни в одной тчк
комплексной обл. Теорема
Лорана. Функция
f(z)
аналитична внутри кольцевой обл K:
r<
R,
то р.Лорана (1) не сход ни в одной тчк
комплексной обл. Теорема
Лорана. Функция
f(z)
аналитична внутри кольцевой обл K:
r<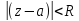 может быть представлена сходящейся в
р.Лорана, коэффиц.которого (2)
может быть представлена сходящейся в
р.Лорана, коэффиц.которого (2)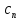 :
: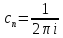
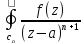 dz;
где
n
dz;
где
n ;
;
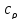 -окружность:
-окружность: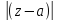 =
=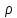 ;Док-во.
Рассмотрим
произвольную тчк z
кольца
К,
удовлетвор.услов:
;Док-во.
Рассмотрим
произвольную тчк z
кольца
К,
удовлетвор.услов:
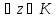 :
: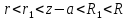 .
Внутри выбранная облf(z),
след-но представлена формулой Коши
f(z)=
.
Внутри выбранная облf(z),
след-но представлена формулой Коши
f(z)=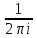
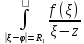 d
d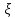 +
+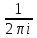
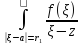 d
d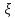 (3);
(3);
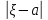 =
= >
>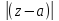 ,
след-но
,
след-но
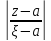 <1;
<1;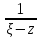 =
=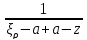 =
= *
*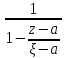 =
=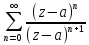 подставив это в (3):f(z)=
подставив это в (3):f(z)=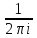
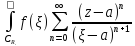 d
d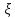 +
+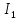 =
=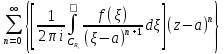 +
+ =
=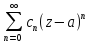 +
+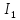 =
=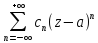 ,
где
,
где
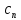 вычисляется по (2); 1-е слагаемое
(1)-Правильная(регулярная) часть р.Лорана,
2-е слааемое(1)- главная часть р.Лорана
вычисляется по (2); 1-е слагаемое
(1)-Правильная(регулярная) часть р.Лорана,
2-е слааемое(1)- главная часть р.Лорана
30.ИОТ:устранимыеОТ,
полюсы и их связь с нулями.f(z)
=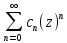 +
+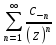 ;
1-е слагаемое-главная часть р.Лорана,
2-е слагаемое- правильная часть р.Лорана.
Тчкz=а
изолированная
особоя тчк f(z),
если:
1.
f(z)
не
определена в тчк
a;
2.
f(z)
является
аналитической в любом кольце вида:0<
;
1-е слагаемое-главная часть р.Лорана,
2-е слагаемое- правильная часть р.Лорана.
Тчкz=а
изолированная
особоя тчк f(z),
если:
1.
f(z)
не
определена в тчк
a;
2.
f(z)
является
аналитической в любом кольце вида:0<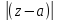 <
<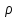 .
Кольцо 0<
.
Кольцо 0<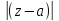 <
<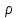 -
проколотая окрестность тчкz=a;
z=a
-
ИОТ f(z)
(изолированная
особая тчк): 1)z=a
устранимая
особая тчк, если существует канонический
предел
-
проколотая окрестность тчкz=a;
z=a
-
ИОТ f(z)
(изолированная
особая тчк): 1)z=a
устранимая
особая тчк, если существует канонический
предел
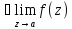 =A
=A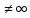 ;
2) z=a
полюс,
если
;
2) z=a
полюс,
если
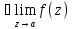 =
=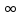 ;
Характер ИОТz=a
;
Характер ИОТz=a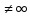 ф-ии
f(z)
может быть установлен по виду р.Лорана
этой ф-ии для кольца
r<
ф-ии
f(z)
может быть установлен по виду р.Лорана
этой ф-ии для кольца
r<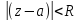 .
ИОТ является:1)устранимой, если главная
часть разложения отсутствует.2)поюсом,
если главная часть содержит конечное
число членов. При этом, если главная
часть р.Лорана имеет вид
.
ИОТ является:1)устранимой, если главная
часть разложения отсутствует.2)поюсом,
если главная часть содержит конечное
число членов. При этом, если главная
часть р.Лорана имеет вид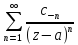
(cm ),число
m
–
порядок полюса z=a(если
m=1,
полюс
назыв. простым). В этом случае
f(z)
может
быть представлена в виде .
f(z)=
),число
m
–
порядок полюса z=a(если
m=1,
полюс
назыв. простым). В этом случае
f(z)
может
быть представлена в виде .
f(z)=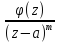 ,где
,где
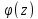 -ф-я,
аналитич. в тчкz=a
и
-ф-я,
аналитич. в тчкz=a
и
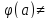 0.
Если для аналитич. ф-и
0.
Если для аналитич. ф-и
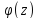 числоz=a
есть
нуль порядка m
,
то для f(z)=
числоz=a
есть
нуль порядка m
,
то для f(z)=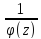 это
число явл. полюсом порядка m.
это
число явл. полюсом порядка m.
31.
СОТ. Р.Лорана для в окрестн.бесконечно
удален.тчк.
z=a
существенно
особая тчк, если не существует предела
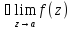 .
Тчкz=a
явл.
СОТ ф-и f(z)
тогда
и только тогда, когда главная часть ее
Лорановского разложения в окрестн.тчк
z=a
содержит
бесконечное множество членов.
.
Тчкz=a
явл.
СОТ ф-и f(z)
тогда
и только тогда, когда главная часть ее
Лорановского разложения в окрестн.тчк
z=a
содержит
бесконечное множество членов.
Если
f(z)-
однозначная аналитическая функция в
области |z| > R,понятие
особой точки можно распространить и на
бесконечно
удаленную точку z=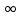 .Она
является устранимой,
если
.Она
является устранимой,
если
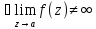 ;
полюсом,
если
;
полюсом,
если
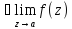 =
=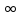 ,существенно
особой, если
,существенно
особой, если
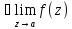 Р.Лорана
f(z)в
окрестн. бесконечно удален.тчк: f(z)=
Р.Лорана
f(z)в
окрестн. бесконечно удален.тчк: f(z)=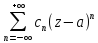 ;
; .Главная
часть-часть, состоящ. из членов с положит.
степенями z,
правильная- часть, содержащ. нулевую и
отрицательн. степени z.
.Главная
часть-часть, состоящ. из членов с положит.
степенями z,
правильная- часть, содержащ. нулевую и
отрицательн. степени z.
32. Вычет аналитических функций.
Пусть
f(z)
аналитична в кольце К:
0<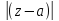 <
<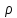 ;
;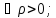 Тогдаz=a
либо ИОТ f(z),
либо
правильная тчк f(z),
след-но в окрестности тчк z=a
f(z)
раскладывается
в сходящийся р.Лорана: f(z)=
Тогдаz=a
либо ИОТ f(z),
либо
правильная тчк f(z),
след-но в окрестности тчк z=a
f(z)
раскладывается
в сходящийся р.Лорана: f(z)=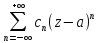 .
Вычет f(z)
в тчк z=a
-
комплексное число, равное коэффициенту
при -1 степени тчк
.
Вычет f(z)
в тчк z=a
-
комплексное число, равное коэффициенту
при -1 степени тчк
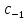 -разложение
функции f(z)
в
р.Лорана в окрестности тчк z=a.
-разложение
функции f(z)
в
р.Лорана в окрестности тчк z=a.
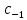 -вычет.
Обозначение:
-вычет.
Обозначение:
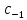 =
=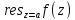 (1).
Т.к. коэффициент р.Лорана:
(1).
Т.к. коэффициент р.Лорана:
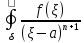 d
d ,
то
,
то
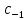 =
=
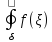 d
d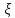 ;
откуда
z=
;
откуда
z=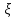 -
-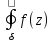 dz=2
dz=2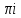 *
*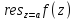 (2);
(2);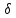 -любой
замкнутый контур, ограничен. тчк a;
-любой
замкнутый контур, ограничен. тчк a;
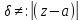 =
=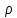 ;
;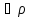 >0.
Из (2) следует, чтоz=a
- правильная
тчк
f(z),
то
>0.
Из (2) следует, чтоz=a
- правильная
тчк
f(z),
то
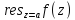 =0.Пусть
z=a
полюс
1-го порядка.Тогда
в окрестн тчк z=a,
f(z)
представлена
р.Лорана: f(z)=
=0.Пусть
z=a
полюс
1-го порядка.Тогда
в окрестн тчк z=a,
f(z)
представлена
р.Лорана: f(z)=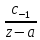 +
+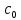 +
+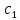 (z-a)+
(z-a)+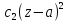 +…(3)Умножим(3)
на
z=a:
(z-a)
*f(z)=
+…(3)Умножим(3)
на
z=a:
(z-a)
*f(z)=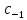 +
+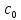 (z-a)+
(z-a)+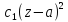 +...;
+...;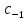 =
=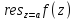 =
= (z-a).Если
f(z)=
(z-a).Если
f(z)=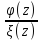 ,
где
,
где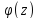 ,
,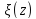 -
функции аналитические.
-
функции аналитические.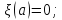
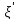 (a)
(a)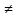 0,
0,
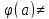 0,тогда
0,тогда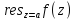 =
=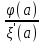 ;Пусть
z=a
полюс
m-го
порядка.
След-но р.Лорана имеет вид: f(z)=
;Пусть
z=a
полюс
m-го
порядка.
След-но р.Лорана имеет вид: f(z)=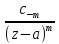 +
+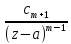 +…+
+…+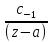 +
+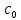 +
+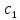 (z-a)+…;умножим
на
(z-a)+…;умножим
на
 :
: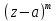 f(z)=
f(z)=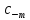 +
+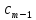 (z-a)+…+
(z-a)+…+ +
+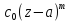 .Дифференцируя
последнее рав-во m-1
раз, получим:
.Дифференцируя
последнее рав-во m-1
раз, получим:
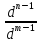 (
(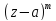 f(z))=(m-1)!
f(z))=(m-1)!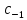 +(m-1)!
+(m-1)!
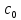 (z-a)+…;
(z-a)+…;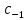 =
=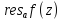 =
=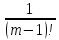
 .
Пусть
z=a
СОТ
.
Пусть
z=a
СОТ
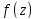 .
Тогда вычет
.
Тогда вычет

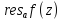 =
=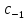 ;Если
z=
;Если
z=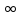 .Вычетом
функции
.Вычетом
функции
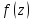 в тчкz=
в тчкz=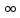 называется
комплексн.число равное коэфф. при -1
степенного разложения в р.Лорана
называется
комплексн.число равное коэфф. при -1
степенного разложения в р.Лорана
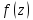 вz=
вz=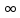 ,
взятый с противоположным знаком:
,
взятый с противоположным знаком:
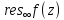 =-
=-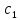 ;
; =
=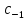 =
-1
=
-1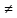 0.
0.
33.
Основная теорема о вычетах. Приложения
вычетов к вычислению комплексных
интегралов. Теорема(осн.
теорема о вычетах). Пусть
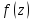 аналитич. в обл D
за исключен. конечного числа z1
,z2
…zn
ИОТ. Кривая
аналитич. в обл D
за исключен. конечного числа z1
,z2
…zn
ИОТ. Кривая
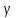 -
простой замкнут.контур, целиком лежащий
в обл.D
и
включающ. в себя все тчк zk
;k=
-
простой замкнут.контур, целиком лежащий
в обл.D
и
включающ. в себя все тчк zk
;k=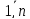 ;Тогда
;Тогда
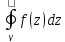 =
=
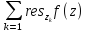
Док-во.
Окружим каждую особую точку zk
окружностью
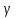 k
столь малого радиуса, чтобы все окружности
k
столь малого радиуса, чтобы все окружности
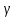 k
лежали
внутри контура
k
лежали
внутри контура
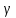 и
не пересекались между собой. Согласно
следствию интегральной теоремы Коши,
имеем
и
не пересекались между собой. Согласно
следствию интегральной теоремы Коши,
имеем
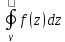 =
=
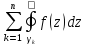 ,
но т.к. внутри окружн.
,
но т.к. внутри окружн.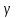 k
, нет
др. ОТ, кроме zk,
,то
k
, нет
др. ОТ, кроме zk,
,то
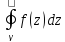 =
=
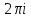
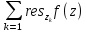 .Следствие:
Пуст
выполняются все условия теоремы. Тогда
сумма вычетов
.Следствие:
Пуст
выполняются все условия теоремы. Тогда
сумма вычетов
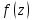 во всех ее ИОТ включаяz=
во всех ее ИОТ включаяz= равна
нулю.
равна
нулю.
 +
+ =0;
Если
=0;
Если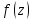 :z1-полюс
1-го порядка;
z2-полюс
4-го порядка; z=
:z1-полюс
1-го порядка;
z2-полюс
4-го порядка; z=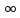 -
правильная тчк, то
-
правильная тчк, то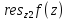 = -
= -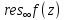 -
- .
1) Если
.
1) Если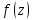 - дробно-рациональная ф-я, аналитич. на
действительной оси и в верхней
полуплоскости (Im
z>0),
за исключением конечного числа ОТ z1
,
…zn,
лежащих в верхней полуплоскости (Im
zk
>0, k=
- дробно-рациональная ф-я, аналитич. на
действительной оси и в верхней
полуплоскости (Im
z>0),
за исключением конечного числа ОТ z1
,
…zn,
лежащих в верхней полуплоскости (Im
zk
>0, k=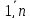 )
и если
)
и если
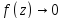 при
при ,
то
,
то =
=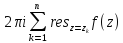 .
2) Если
.
2) Если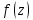 - дробно-рациональная ф-я, аналитич. на
действит. оси и в верхней полуплоскости,
за исключ. конечного числа тчкz1
,
…zn
, лежащих в верхней полуплоскости, и
если
- дробно-рациональная ф-я, аналитич. на
действит. оси и в верхней полуплоскости,
за исключ. конечного числа тчкz1
,
…zn
, лежащих в верхней полуплоскости, и
если
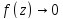 при
при
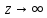 ,
то для любого
,
то для любого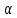 >0:
>0: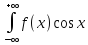 dx=
dx=
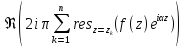 ;
;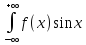 dx=
Im
dx=
Im
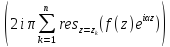 .
.
34.Приложения
вычетов к вычислению определенных
интегралов.
Если
 – рациональн.ф-я от
– рациональн.ф-я от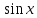 ,
,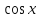 ,
непрерывная при 0<x<2
,
непрерывная при 0<x<2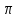 ,
то сделав подстановку
,
то сделав подстановку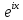 =z,
получим:
=z,
получим:
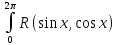 dx
=
dx
=
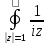 R
R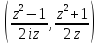 dz.
Значение интеграла в правой части равно
сумме вычетов подынтегральной ф-ии
относит.полюсов, лежащих внутри окружности
dz.
Значение интеграла в правой части равно
сумме вычетов подынтегральной ф-ии
относит.полюсов, лежащих внутри окружности
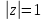 ,
умноженной на
,
умноженной на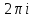 .
.
