
- •1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- •2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
- •2.Однородные ду
- •5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
- •8.Линейная зависимость,независимость ф-ий. Определитель вронского.
- •9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
- •12Линейные однородные системы ду высших порядков с постоянными коэффициентами
- •13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
- •15 Устойчивость по Ляпунову
- •16 Устойчивость по первому приближению
- •19.Предел и непрерывность функций комплексной переменной.
- •22.Элеменарные функции комплексной переменной.
- •25.Теорема Коши и интегральная формула Коши.
- •26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
- •27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
- •28. Нули аналитических функций. И их классификация.
- •29. Ряд Лорана. Изолированные особые точки и их классификация.
- •32. Вычет аналитических функций.
- •35.Классификац.Ур. Матфизики.
- •42. Оригинал и изображение. Св-ва преобразования Лапласа: линейность, подобие.
- •44. Формулы обращения преобразования Лапласа.
- •45. Применение преобразования Лапласа: теоремы обращения.
- •46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
- •47. Применение преобразования Лапласа к решению физических задач.
- •48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
8.Линейная зависимость,независимость ф-ий. Определитель вронского.
Систему
функций
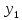 (x),
(x),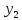 (x),…,
(x),…,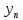 (x)
наз. линейно зависимой на I,
если сущ-ют постоянные числа
(x)
наз. линейно зависимой на I,
если сущ-ют постоянные числа
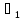 ,
,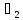 ,…,
,…,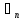 хотябы одно из которых отлично от нуля,
что выполняется :
хотябы одно из которых отлично от нуля,
что выполняется :
 (x)+
(x)+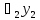 (x)+…+
(x)+…+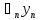 (x)=0,
(x)=0,
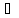 x
x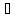 (a,b)-----(1);
Если (1) имеет место только при
(a,b)-----(1);
Если (1) имеет место только при
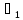 =
=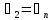 =0,
то система ф-й
=0,
то система ф-й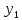 (x),
(x),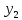 (x),…,
(x),…, (x)
наз.линейно независимой на I.
(x)
наз.линейно независимой на I.
Рассмотрим
систему n
ф-й
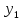 (x),
(x),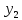 (x),
(x),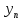 (x)
непрерывных вместе со своими производными
до порядка (n-1)включительно
на I.
Определитель Вронского W
(x)
непрерывных вместе со своими производными
до порядка (n-1)включительно
на I.
Определитель Вронского W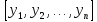 этой системы ф-й называется определитель:
этой системы ф-й называется определитель:
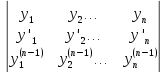 ;1)
Если
ф-и
;1)
Если
ф-и
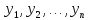 лин.зависимые на интервалеI,
то опред.вронского W
равен нулю на этом I.
лин.зависимые на интервалеI,
то опред.вронского W
равен нулю на этом I.
2)Если
опред.вронского составленный для решений
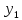 и
и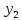 ДУy
‘’+py
‘+qy=0,
не равен нулю при x=
ДУy
‘’+py
‘+qy=0,
не равен нулю при x= ,
то он не обращается в ноль ни при одном
значенииx
из этого интервала.
,
то он не обращается в ноль ни при одном
значенииx
из этого интервала.
3)Если
 и
и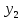 решения ур-яy
‘’+py
‘+qy=0,
линейно независимые на интервале I,
то W,
составленный из этих решений,не обращается
в нуль ни в одной точке этого интервала
решения ур-яy
‘’+py
‘+qy=0,
линейно независимые на интервале I,
то W,
составленный из этих решений,не обращается
в нуль ни в одной точке этого интервала
9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
Систему
ф-ий
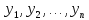 ,
являющихся линейно независимыми
решениями у-я
,
являющихся линейно независимыми
решениями у-я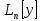 =0,
называют фундамент.системой решений
этого у-я. Для такой системы вронскиан:
=0,
называют фундамент.системой решений
этого у-я. Для такой системы вронскиан:
W(x)=W 0;
0;
Теорема
1. Если
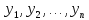 —фунд.
сист. реш.однор.ДУ
—фунд.
сист. реш.однор.ДУ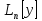 =0,
то его общее решение имеет вид (1):y=
=0,
то его общее решение имеет вид (1):y=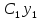 +
+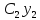 +…+
+…+ ,
где
,
где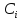 --
произвольные постоянные,i=
--
произвольные постоянные,i= .
.
Док-во:
выражение (1) является решением у-я
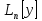 =0
на основании свойств лин.диф-ного
оператора. Докажем, что еслиy=
=0
на основании свойств лин.диф-ного
оператора. Докажем, что еслиy=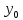 ,y’=
,y’=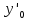 ,…,
,…,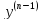 =
=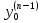 ---(2),
приx=
---(2),
приx=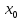 ,
то
,
то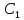 ,
,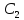 ,…,
,…,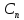 можно подобрать таким образом, что (1)
будет удовл. усл. (2). Подставляя в (1)x=
можно подобрать таким образом, что (1)
будет удовл. усл. (2). Подставляя в (1)x=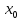 и обозначая
и обозначая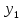 (
(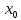 )=
)=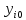 ,i=
,i=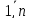 получим систему лин. алгебр.у-й:
получим систему лин. алгебр.у-й:
 ;
Эта система имеет единств.решение относ.
неизв.
;
Эта система имеет единств.решение относ.
неизв.
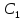 ,
,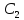 ,…,
,…, при котором (1) удовл. (2)
при котором (1) удовл. (2)
10 . Линейные неоднородные ур-я с постоянными коэф-ми. Ур-ия со спец правой частью. Уравнение вида:
y(n)+a1y(n-1)+…+an-1y’+any=f(x) (1)
называется
линейн. не однородным ур-ем n-го
порядка с постоянными коэффициентами,
где a1,а2,…аn-постоянные
вещественные коэффициенты. Общее решение
ур-я (1) равно сумме какого-либо его
частного решения и общего решения
соответствующего ему однородного ур-я.
Решение ур-я (1) следует искать в виде:
y(x)=y*
+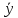 , где y*-
частное решение ур-я (1);
, где y*-
частное решение ур-я (1);
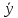 -
общее;В некоторых случаях, для определения
y*
используют метод неопределенных
коэффициентов(метод подбора):
-
общее;В некоторых случаях, для определения
y*
используют метод неопределенных
коэффициентов(метод подбора):
Пусть правая часть ур-я (1) имеет вид:
f(x)=eαx[Pl(x)cosβx+Qm(x)sinβx], (2)
где
Pl(x)
и Qm(x)
– многочлены степени l
и
m
соответственно, тогда y*
ур-я (1) примет вид: y*(x)=xs
eαx[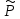 k(x)cosβx+
k(x)cosβx+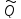 k(x)
sinβx],
(3)
k(x)
sinβx],
(3)
где
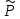 k(x),
k(x),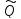 k(x),
k=max(l,m)-многочлены
k-ой
степени от x
с неопределенными коэф-ми, а s-кратность
корня λ=α+iβ
характеристического уравнения, причем,
если α+iβ
не явл. Корнем характер-го ур-я, то s=0.
Таблица:
1-й столбец «Правая частьДУ»; 2-й «Корни
характеристического ур-ия»; 3-й «Виды
частного решения» соответственно:
k(x),
k=max(l,m)-многочлены
k-ой
степени от x
с неопределенными коэф-ми, а s-кратность
корня λ=α+iβ
характеристического уравнения, причем,
если α+iβ
не явл. Корнем характер-го ур-я, то s=0.
Таблица:
1-й столбец «Правая частьДУ»; 2-й «Корни
характеристического ур-ия»; 3-й «Виды
частного решения» соответственно:
I.
Pm(x)
=> 1.Число 0 не является корнем харак-го
ур-я =>
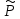 m(x)
m(x)
I.
2. Число 0 – корень харак-го ур-я кратности
s
=> xs m(x)
m(x)
II.
Pm(x)eαx
=> 1.Число α не явл. Корне хар-го ур-я =>
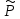 m(x)
eαx
m(x)
eαx
II.
2.
Число α – корень харак-го ур-я кратности
s
=>xs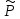 m(x)
eαx
m(x)
eαx
III.
Pl(x)cosβx+Qm(x)sinβx
=> 1.Число +iβ
не является корнем харак-го ур-я =>
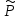 k(x)cosβx+
k(x)cosβx+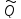 k(x)
sinβx,
k=
max(l,m)
k(x)
sinβx,
k=
max(l,m)
III.
2. Число +iβ
– корень харак-го ур-я кратности s
=> xs(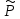 k(x)cosβx+
k(x)cosβx+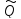 k(x)
sinβx)
k(x)
sinβx)
IV.
eαx(Pl(x)cosβx+Qm(x)sinβx)=>
1.Число
α+iβ
не является корнем харак-го ур-я =>
(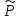 k(x)cosβx+
k(x)cosβx+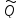 k(x)
sinβx)eαx
k(x)
sinβx)eαx
IV.
2.Число
α+iβ
– корень харак-го ур-я кратности s
=> xs(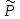 k(x)cosβx+
k(x)cosβx+ k(x)
sinβx)eαx
k(x)
sinβx)eαx
