
- •1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- •2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
- •2.Однородные ду
- •5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
- •8.Линейная зависимость,независимость ф-ий. Определитель вронского.
- •9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
- •12Линейные однородные системы ду высших порядков с постоянными коэффициентами
- •13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
- •15 Устойчивость по Ляпунову
- •16 Устойчивость по первому приближению
- •19.Предел и непрерывность функций комплексной переменной.
- •22.Элеменарные функции комплексной переменной.
- •25.Теорема Коши и интегральная формула Коши.
- •26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
- •27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
- •28. Нули аналитических функций. И их классификация.
- •29. Ряд Лорана. Изолированные особые точки и их классификация.
- •32. Вычет аналитических функций.
- •35.Классификац.Ур. Матфизики.
- •42. Оригинал и изображение. Св-ва преобразования Лапласа: линейность, подобие.
- •44. Формулы обращения преобразования Лапласа.
- •45. Применение преобразования Лапласа: теоремы обращения.
- •46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
- •47. Применение преобразования Лапласа к решению физических задач.
- •48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
22.Элеменарные функции комплексной переменной.
Следующие функции (как однозначные, так и многозначные) называются основными элементарными:
1.
Дробно-рациональная функция (a0zn
+ a1zn-1
+…+ an)/(b0zm
+ b1zm-1
+…+ bm),
n,m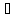 N.
Частными случаями этой функции являются:
N.
Частными случаями этой функции являются:
а)
линейная функция az
+ b,
a,b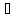 C,
а≠0;
C,
а≠0;
б)
степенная функция zn,
п
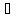 N ;
N ;
в)
дробно-линейная функция (az+b)/cz+d)
a,b,c,d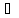 C,
с≠0,
ad
- bc
≠ 0;
C,
с≠0,
ad
- bc
≠ 0;
г) функция Жуковского (z + 1/z )/2.
2. Показательная функция ez =ех+iу = ex(cosy + isiny). Функция ez обладает свойствами:
1) eZ1+Z2 = ez1eZ2, для любых чисел z1, z2;
2) еz - периодическая с периодом 2πi, т.е. еz = еz+2лi;
3)
ez
непрерывна
на всей комплексной плоскости
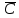 ;
;
4) для любого комплексного z = x + iy справедливы равенства:
│е2│= ех; arg ez = у.
3. Тригонометрические функции: cosz= (eiz + e-iz)/2; sinz= (eiz - e-iz)/2i; tgz = sinz/cosz; ctgz = cosz/sinz;
4. Гиперболические функции: sh z = (ez – e-z)/2; chz= (ez + e-z)/2; thz = shz/chz; cthz=chz/shz;
5.
Логарифмическая функция Ln
z
= In
│z│
+
i(arg
z
+ 2πk),
к Z.
Функция
Ln
z
является
многозначной. В каждой точке z,
отличной от 0 и
Z.
Функция
Ln
z
является
многозначной. В каждой точке z,
отличной от 0 и
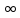 ,
она принимает бесконечно много значений.
Выражениеln|z|
+ iargz
называется главным
значением логарифмической функции и
обозначается через ln
z.
Таким образом, Ln
z
= In
z
+ 2πk
i,
k
,
она принимает бесконечно много значений.
Выражениеln|z|
+ iargz
называется главным
значением логарифмической функции и
обозначается через ln
z.
Таким образом, Ln
z
= In
z
+ 2πk
i,
k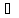 Z
.
Z
.
6.
Общая степенная функция za=
eaLnz,
a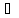 C
. Эта
функция многозначная, ее главное значение
равно ealnz.
C
. Эта
функция многозначная, ее главное значение
равно ealnz.
Если
а=1/n,
n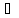 N,
то получаем многозначную функцию -
корень n-ой
степени из комплексного числа:Z1/n=
N,
то получаем многозначную функцию -
корень n-ой
степени из комплексного числа:Z1/n=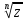 =e(ln│z│
+ i(argz
+ 2πk))/n
=
=e(ln│z│
+ i(argz
+ 2πk))/n
=
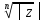 e
i(argz
+ 2πk)/n,
k
e
i(argz
+ 2πk)/n,
k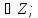
7.
Общая показательная функция аz
=ezLna,
а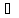 С.
С.
Главное значение этой многозначной функции равно ezlna. В дальнейшем при а > 0 полагаем az = ezlnа.
8.
Обратные тригонометрические функции:
Arcsin
z
= -iLn(iz
+ (l-z2)1/2),
Arccosz
= -iLn(
z
+ (z2-1)1/2);
Arctgz
= -i(Ln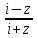 )/2
где (z≠
)/2
где (z≠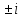 );Arcctgz
= i(Ln
);Arcctgz
= i(Ln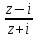 )/2
где (z≠
)/2
где (z≠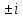 );
и обратные гиперболические функции:Arcshz
= Ln(
z
+ (z2+1)1/2);
Arcchz
= Ln(
z
+ (z2-1)1/2);
Arcth
z
= (Ln
);
и обратные гиперболические функции:Arcshz
= Ln(
z
+ (z2+1)1/2);
Arcchz
= Ln(
z
+ (z2-1)1/2);
Arcth
z
= (Ln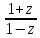 )/2;
Arccth
z
= (Ln
)/2;
Arccth
z
= (Ln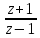 )/2;Все
эти функции многозначны.
)/2;Все
эти функции многозначны.
24.Интеграл
от функции комплексной переменной.Прмиеры.Пусть
функция f (z) – определена и непрерывна
в области G,
а Г – кусочно-гладкая кривая, лежащая
в области G;z=x+iy,
f(z)=u+iv, где u=u(x,y), v=v(x,y) – действительные
функции переменных x и y. Вычисление
интеграла от функции w=f(z) сводится к
вычислению криволинейных интегралов
второго рода
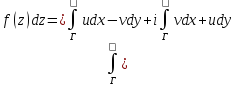 Если
кривая задана параметрическими
уравнениями x=x(t), y=y(t), а начальная
и конечная точки дуги соответствуют
значениям t=a, t=b, то
Если
кривая задана параметрическими
уравнениями x=x(t), y=y(t), а начальная
и конечная точки дуги соответствуют
значениям t=a, t=b, то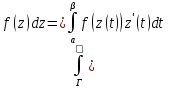 где z(t)=x(t)+iy(t).
где z(t)=x(t)+iy(t).
Пусть
Г – кусочно-гладкая кривая, состоящая
из гладких частей Г1, Г2...Гn. Тогда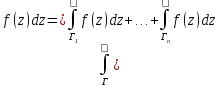
Пример:Вычислить
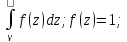
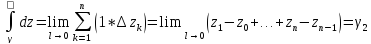 =>
=> Следовательно
- решеню интеграла не зависит от пути
интегрированияи равен 0 вдоль любой
замкнутой прямой.
Следовательно
- решеню интеграла не зависит от пути
интегрированияи равен 0 вдоль любой
замкнутой прямой.
25.Теорема Коши и интегральная формула Коши.
Пусть функция f (z) – определена и непрерывна в области G, а Г – кусочно-гладкая кривая, лежащая в области G;z=x+iy, f(z)=u+iv, где u=u(x,y), v=v(x,y) – действительные функции переменных x и y.
Теорема: Если
f(z) является аналитической функцией в
некоторой односвязной области G,
ограниченной кусочно-гладкой кривой
Г, и на самой кривой, то
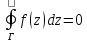 (теорема
Коши),и для любой внутренней точки
(теорема
Коши),и для любой внутренней точки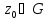 имеем
имеем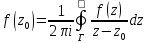 (интегральная
формула Коши).
(интегральная
формула Коши).
Доказательство:
Согласно
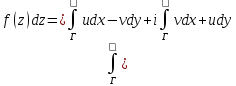 имеем
интеграл по контуру
имеем
интеграл по контуру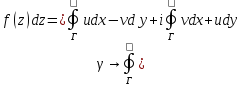 т.кf(z)
аналитична в G
то ее дейст.часть u(x,y)
и мнимая v(x,y)
являются функц. Непрерывными в G
и в G
существ. Непрерывные частные производные
т.кf(z)
аналитична в G
то ее дейст.часть u(x,y)
и мнимая v(x,y)
являются функц. Непрерывными в G
и в G
существ. Непрерывные частные производные
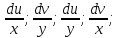 -> дляинегр. Стоящив в прав. части
равенства имеет место формула Грина:
-> дляинегр. Стоящив в прав. части
равенства имеет место формула Грина: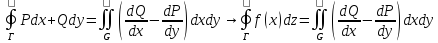 ;
;
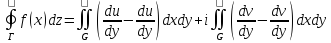 =
0. То что треб. доказ.
=
0. То что треб. доказ.
Кроме
того, справедлива формула
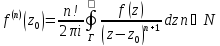
Из
теоремы Коши следует, что если w=f(z) –
аналитическая функция в односвязной
области G, то интеграл 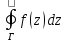 не
зависит от пути интегрирования Г (зависит
только от начальной и конечной точек).
В этом случае для вычисления интеграла
применяется формула Ньютона-Лейбница:
не
зависит от пути интегрирования Г (зависит
только от начальной и конечной точек).
В этом случае для вычисления интеграла
применяется формула Ньютона-Лейбница:
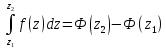 гдеF(z)
– какая-либо первообразная функции
f(z), т. е. F'(z)=f(z).
гдеF(z)
– какая-либо первообразная функции
f(z), т. е. F'(z)=f(z).
