- •1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- •2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
- •2.Однородные ду
- •5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
- •8.Линейная зависимость,независимость ф-ий. Определитель вронского.
- •9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
- •12Линейные однородные системы ду высших порядков с постоянными коэффициентами
- •13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
- •15 Устойчивость по Ляпунову
- •16 Устойчивость по первому приближению
- •19.Предел и непрерывность функций комплексной переменной.
- •22.Элеменарные функции комплексной переменной.
- •25.Теорема Коши и интегральная формула Коши.
- •26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
- •27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
- •28. Нули аналитических функций. И их классификация.
- •29. Ряд Лорана. Изолированные особые точки и их классификация.
- •32. Вычет аналитических функций.
- •35.Классификац.Ур. Матфизики.
- •42. Оригинал и изображение. Св-ва преобразования Лапласа: линейность, подобие.
- •44. Формулы обращения преобразования Лапласа.
- •45. Применение преобразования Лапласа: теоремы обращения.
- •46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
- •47. Применение преобразования Лапласа к решению физических задач.
- •48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
12Линейные однородные системы ду высших порядков с постоянными коэффициентами
Нормальной
системой ДУ n-го
порядка наз систему вида:
 1=f1(t,x1,…,xn),
1=f1(t,x1,…,xn),
………………………,
(1)
 n=fn(t,x1,…,xn)
n=fn(t,x1,…,xn)
Или
в векторной форме:
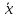 =f(t,x)
=f(t,x)
Порядком
нормальной системы называется число
входящих в нее уравнений. Линейной
системой ДУ наз. система:
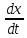 i=
i= ij(t)xj+fi(t),
i=
ij(t)xj+fi(t),
i=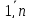 ,i=
,i=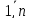 ,
,
 =Ax+f(t)
(2)
=Ax+f(t)
(2)
a11(t) a12(t) … a1n(t)
A= a21(t) a22(t) … a2n(t) (2)
…………………………....
am1(t) am2(t) … amn(t)
Если в (2) f(t)=0, то соотв. Система наз. однородной.
Совокупность n-функций
X1=ф1(t), x2=ф2 (t),…,xn=фn(t) определенных и непрерывно диф-мых на (a;b), наз. решением системы (1) если она обращает в тождество каждое ур-е этой системы.
Рассмотрим систему:
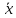 =Ax
a11(t)
a12(t)
… a1n(t)
=Ax
a11(t)
a12(t)
… a1n(t)
x1 A a21(t) a22(t) … a2n(t) (3)
x= x2 …………………………....
… am1(t) am2(t) … amn(t)
xn
aijЄR
; i=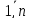 ;
j=
;
j=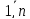
(3) – линейная однородная система с постоянными коэффициентами.
13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
Линейной
yнеоднородной
системой ДУ называется система вида:
dxi/dt=
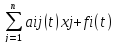
 ,
гдеi=1,2,…,n,
j
= 1, 2, …,n.
Или в матричной форме
,
гдеi=1,2,…,n,
j
= 1, 2, …,n.
Или в матричной форме
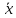 =Ax
+ f(t),
где A
=
=Ax
+ f(t),
где A
=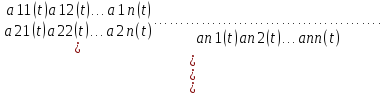 .
Если f(t) равно 0, то соответствующая
система называется однородной.
Совокупность n-функций x1=
φ1(t),
x2=
φ2(t),
…, xn=
φn(t)
определённых и непрерывно дифференцируемых
на интервале (a,b) называется решением
системы
.
Если f(t) равно 0, то соответствующая
система называется однородной.
Совокупность n-функций x1=
φ1(t),
x2=
φ2(t),
…, xn=
φn(t)
определённых и непрерывно дифференцируемых
на интервале (a,b) называется решением
системы
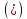 ,
если она обращает в тождество каждое
уравнение данной системы. Задача Коши
для системы
,
если она обращает в тождество каждое
уравнение данной системы. Задача Коши
для системы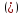 :
необходимо найти решения x1=
х1(t),
x2=
х2(t),
…, xn=
хn(t)
системы
:
необходимо найти решения x1=
х1(t),
x2=
х2(t),
…, xn=
хn(t)
системы
 удовлетворяющее условиям x1=
х10(t),
x2=
х20(t),
…, xn=
хn0(t),
при t→t0.
удовлетворяющее условиям x1=
х10(t),
x2=
х20(t),
…, xn=
хn0(t),
при t→t0.
Рассмотрим
систему
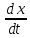 =Ax
+ f(t)
(1),
где A
-
постоянная матрица.Для нахождения
общего решения системы (1), кроме общего
решения соответствующей ей однородной
системы, нужно знать какое-либо частное
решение неоднородной системы (1). Одним
из методов нахождения частного решения
является метод подбора или, иначе, метод
неопределенных коэффициентов. Применение
этого метода возможно в том случае,
когда входящая в систему вектор-функция
f(t)
является
функцией специального вида. Имеет место
следующее правило. Пусть вектор-функция
f(t)
имеет вид f(t)
= eαt[Pl(t)cosβt
+ Qm(t)sinβt],
где
α,β-
заданные действительные числа, Pl(t),
Qm(t)
–
вектор функции, с компонентами в виде
многочленов переменной t,
степени которых равны или меньше,
соответственно, l
и т.
Частное
решение неоднородной системы (1) в этом
случае ищется в виде: x*(t)=
eαt[Rq+s(t)cosβt
+ Tq+s(t)sinβt],
=Ax
+ f(t)
(1),
где A
-
постоянная матрица.Для нахождения
общего решения системы (1), кроме общего
решения соответствующей ей однородной
системы, нужно знать какое-либо частное
решение неоднородной системы (1). Одним
из методов нахождения частного решения
является метод подбора или, иначе, метод
неопределенных коэффициентов. Применение
этого метода возможно в том случае,
когда входящая в систему вектор-функция
f(t)
является
функцией специального вида. Имеет место
следующее правило. Пусть вектор-функция
f(t)
имеет вид f(t)
= eαt[Pl(t)cosβt
+ Qm(t)sinβt],
где
α,β-
заданные действительные числа, Pl(t),
Qm(t)
–
вектор функции, с компонентами в виде
многочленов переменной t,
степени которых равны или меньше,
соответственно, l
и т.
Частное
решение неоднородной системы (1) в этом
случае ищется в виде: x*(t)=
eαt[Rq+s(t)cosβt
+ Tq+s(t)sinβt],
где
q=max (l,m), s =

Rq+s, Tq+s _ вектор функции, компонентами которых являются многочлены степени q + s с неопределенными коэффициентами.
15 Устойчивость по Ляпунову
Рассмотрим
систему ДУ
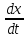 =f(x,y)
(1)
=f(x,y)
(1)
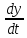 =g(x,y)
=g(x,y)
где f(x,y) и g(x,y)непрерывно диф-ые ф-ии в некоторой области D плоскости Оху. (Оху- будет фазовой плоскостью).
Точками покоя (или положениями равновесия) системы (1) будут точки (х;у), в которых выполняются соотношения: f(x,y)=0, п(x,y)=0.
Пусть g(0,0)=f(0,0)=0, т.е. О(0;0) явл. Точкой покоя системы (1).
Точка покоя х=у=0 системы (1) устойчива по Ляпунову, если каково бы ни было ε>0, можно найти такое δ=δ(ε)>0, что для любого решения (x(t);y(t)), начальные данные которого х(0)=х0, у(0)=у0 удовлетворяют условию
Iх0I<δ, Iу0I<δ, (2)
выполняются неравенства
Ix(t)I<ε,
Iy(t)I<ε
для всех t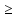 0.
(3)
0.
(3)
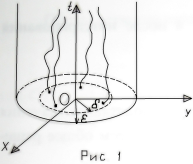
Каким
бы узким ни был цилиндр радиуса ε и осью
Оt,
в плоскости t=0
найдется δ окрестность точки О(0;0;0)
такая, что все интегральные кривые
x=x(t),
y=y(t),
выходящие из этой окрестности, для всех
t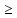 0
будут оставаться внутри этого
цилиндра(рис1). Если, кроме выполнения
неравенств (3), выполняется также условие
0
будут оставаться внутри этого
цилиндра(рис1). Если, кроме выполнения
неравенств (3), выполняется также условие
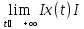 =
=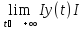 =0,
то говорят, что точка покоя асимптотически
устойчива.
=0,
то говорят, что точка покоя асимптотически
устойчива.
Точка покоя х=у=0 неустойчивая, если при сколь угодно малом δ>0 хотя бы для одного решения (x(t); y(t)) условие (3) выполняется.