
- •1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- •2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
- •2.Однородные ду
- •5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
- •8.Линейная зависимость,независимость ф-ий. Определитель вронского.
- •9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
- •12Линейные однородные системы ду высших порядков с постоянными коэффициентами
- •13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
- •15 Устойчивость по Ляпунову
- •16 Устойчивость по первому приближению
- •19.Предел и непрерывность функций комплексной переменной.
- •22.Элеменарные функции комплексной переменной.
- •25.Теорема Коши и интегральная формула Коши.
- •26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
- •27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
- •28. Нули аналитических функций. И их классификация.
- •29. Ряд Лорана. Изолированные особые точки и их классификация.
- •32. Вычет аналитических функций.
- •35.Классификац.Ур. Матфизики.
- •42. Оригинал и изображение. Св-ва преобразования Лапласа: линейность, подобие.
- •44. Формулы обращения преобразования Лапласа.
- •45. Применение преобразования Лапласа: теоремы обращения.
- •46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
- •47. Применение преобразования Лапласа к решению физических задач.
- •48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
35.Классификац.Ур. Матфизики.
F(x1,…xn,u,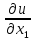 …
… …
…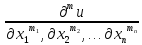 )=0(1);m1+m2+…+mn=m;
Ур(1)
связывающее
искомую функцию и,
независимые
переменные х1...хп
и
частные производные искомой функции
по этим независимым
переменным, называется дифференциальным
уравнением в частных производных.
Здесь
F—
известная
функция своих аргументов.
Наивысший
порядок частных производных, входящих
в уравнение
(1),
называется
порядком
этого
уравнения.
Решением
уравнения (1) в некоторой области D
называется любая функция u=u(x1…xn),
необходимое число раз дифференцируемая
и обращающая его в тождество. (1)—линейное,
если
неизвестн. ф-я и ее частные производные
входят в него линейным образом. Линейн.
ур. 2-го порядка с постоянн.коэффиц. имеет
вид:
)=0(1);m1+m2+…+mn=m;
Ур(1)
связывающее
искомую функцию и,
независимые
переменные х1...хп
и
частные производные искомой функции
по этим независимым
переменным, называется дифференциальным
уравнением в частных производных.
Здесь
F—
известная
функция своих аргументов.
Наивысший
порядок частных производных, входящих
в уравнение
(1),
называется
порядком
этого
уравнения.
Решением
уравнения (1) в некоторой области D
называется любая функция u=u(x1…xn),
необходимое число раз дифференцируемая
и обращающая его в тождество. (1)—линейное,
если
неизвестн. ф-я и ее частные производные
входят в него линейным образом. Линейн.
ур. 2-го порядка с постоянн.коэффиц. имеет
вид:
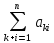
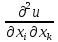 +
+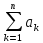
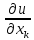 +a0u=f(2),aki,
ak
,a0
+a0u=f(2),aki,
ak
,a0 R;
R;
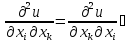 aki=aik;
Рассмотрим (2) u=u(x,y);
a11
aki=aik;
Рассмотрим (2) u=u(x,y);
a11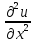 +2a12
+2a12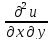 +a22
+a22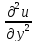 +a1
+a1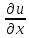 +a2
+a2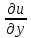 +a0u=f(x,y)(3)
; a11
, a12,
a22,
a2,
a1,
a0
+a0u=f(x,y)(3)
; a11
, a12,
a22,
a2,
a1,
a0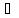 R,
f(x,y)-заданная
ф-я, ур(3) соответсвует квадратичн. форма:
(z1,z2)=a11
(z1)2+
2a12z1z2+a22(z2)2(4)
R,
f(x,y)-заданная
ф-я, ур(3) соответсвует квадратичн. форма:
(z1,z2)=a11
(z1)2+
2a12z1z2+a22(z2)2(4) где
a12=a21
ур
(3)класисифицир.
от собственн. значений
где
a12=a21
ур
(3)класисифицир.
от собственн. значений
 ,
,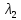 матрицы А. Классификация:1)ур (3)-ур
эллиптического типа, если
матрицы А. Классификация:1)ур (3)-ур
эллиптического типа, если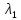 *
*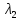 >0.
2)ур(3)- ур гиперболического типа, если
>0.
2)ур(3)- ур гиперболического типа, если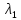 *
*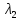 <0.
3)ур(3)- ур параболического типа. если
<0.
3)ур(3)- ур параболического типа. если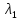 *
*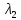 =0.
=0.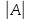 =
a11
* a22
–(a12)2=
=
a11
* a22
–(a12)2=
 *
*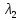 ,то:
1)
,то:
1) *
*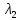 =
a11
* a22
–(a12)2>0
(3)элептический
вид, применим линейную замену переменных
=
a11
* a22
–(a12)2>0
(3)элептический
вид, применим линейную замену переменных
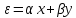 ;
;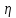 =
=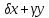 ,получим:
,получим: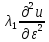 +
+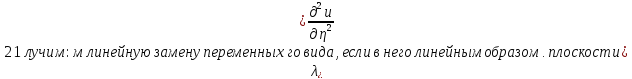 =f(
=f(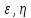 ,
,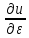 ,
,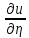 )2)Если
)2)Если
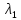 *
*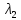 =
a11
* a22
–(a12)2<0
(3)сводится
к
=
a11
* a22
–(a12)2<0
(3)сводится
к
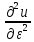 -a
-a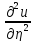 =
f(
=
f(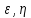 ,
,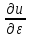 ,
, );a2=-
);a2=-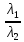 >0
3)a11
* a22
–(a12)2=0,
>0
3)a11
* a22
–(a12)2=0,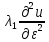 =f(
=f(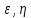 ,
, ,
,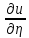 );
);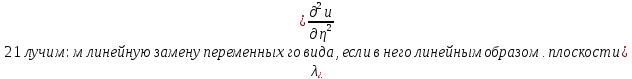 =f(
=f(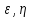 ,
,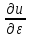 ,
,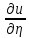 ).При
этом ур.
).При
этом ур.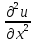 -
-
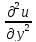 =f(
=f(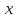 ,y,u,
,y,u,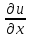 ,
,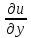 )либо
)либо
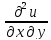 =
f(
=
f( ,y,u,
,y,u,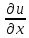 ,
, )-канонич.ур.
гиперболич.типа.
)-канонич.ур.
гиперболич.типа.
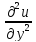 =
f(
=
f(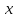 ,y,u,
,y,u, ,
,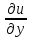 )-канонич.ур.
гиперболич.типа.
)-канонич.ур.
гиперболич.типа.
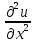 +
+
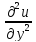 =f(
=f(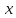 ,y,u,
,y,u,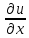 ,
,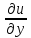 )-канонич.ур.
элиптич.типа.
)-канонич.ур.
элиптич.типа.
36.Приведение
ур. к кононическому виду
можно осуществить либо при помощи
преобраз. Квадрат. Формы Q( )=
)=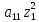 +2
+2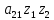 +
+ (1) к ортогональн. виду, либо при помощи
нелинейной замены переменных с помощью
характеристик. Для этого сост. харак.
ур.
(1) к ортогональн. виду, либо при помощи
нелинейной замены переменных с помощью
характеристик. Для этого сост. харак.
ур.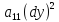 -2
-2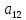 dxdy+
dxdy+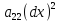 (2)-ур.
Характеристик,распадается на 2 ур.
(2)-ур.
Характеристик,распадается на 2 ур.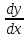 =
=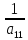 (
(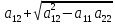 )
(3),
)
(3),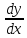 =
=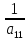 (
(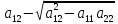 )
(4). Пусть
)
(4). Пусть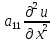 +2
+2 +
+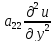 +
+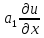 +
+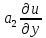 (5)-ур.
гиперболич. типа
(5)-ур.
гиперболич. типа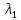
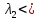 0;
0;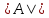 0A=
0A=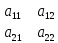 ,
где
,
где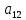 =
=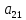
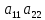 -
-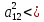 0
0 Д>0
и (2) имеет 2 действит. корня ур. харак.
зад. 2-мя интегралами:u(x,y)=
Д>0
и (2) имеет 2 действит. корня ур. харак.
зад. 2-мя интегралами:u(x,y)=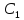 ;
;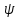 (x,y)=
(x,y)=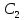 ,
в этом случае в (5) делают замену переем.
ξ=
,
в этом случае в (5) делают замену переем.
ξ=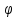 (x,y);
η=
(x,y);
η=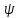 (x,y)
котор. приводит (5) к кононич. виду. Если
(5) –параболического типа
(x,y)
котор. приводит (5) к кононич. виду. Если
(5) –параболического типа
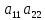 -
-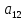 =0,
Д=0, ур. характ.
=0,
Д=0, ур. характ. F(
F(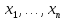 ,u,
,u,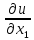 …
…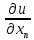 …
…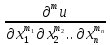 интегр.u(x,y)=C.
интегр.u(x,y)=C.
Замена:
ξ=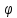 (x,y);
η=
(x,y);
η=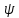 (x,y),
где
(x,y),
где
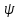 (x,y)-
некот. произв. ф-ция,для которой
(x,y)-
некот. произв. ф-ция,для которой
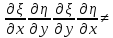 0,
затем (5) прив. к конон. виду , если
(5)-элиптич. типа
0,
затем (5) прив. к конон. виду , если
(5)-элиптич. типа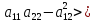 0⇒Д
0⇒Д 0
(2)имеет комплекс. ур. характер.
0
(2)имеет комплекс. ур. характер.
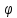 (x,y)
(x,y)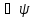 (x,y)=
(x,y)=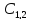 ,
,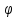 ,
,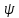 -действит.
ф-ции.
-действит.
ф-ции.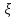 =
=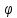 (x,y);
η=
(x,y);
η=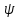 (x,y)
(5) прив. к канон. виду. Дополнит. условия:
1. начальные u(x,t)
(x,y)
(5) прив. к канон. виду. Дополнит. условия:
1. начальные u(x,t)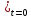 =0, (f(x));
=0, (f(x));
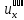 (x,t)
(x,t)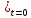 =0(g(x));2.граничные(краевые)
u(x,t)
=0(g(x));2.граничные(краевые)
u(x,t) ,s=
,s=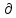 Д
Д
37-1.Ур-ние
колебания струны,теплопроводности.Струна
длиной
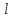 натянута с силой
натянута с силой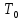 и находиться в прямолин. положении
равновесия в момент врем.t=0.Точкам
струны сообщ. начальн. скорость и
отклонение. Выведем ур-ние малых
поперечных колебаний струны при t>0,если
концы струны:a)закреплены
жёстка,б)свободно, в)закреплены
упруго,г)двигаються в поперечном
направлении по заданным законам .Пусть
Ох совпадает с направл. струны в положении
равновесия. Силы натяжения и силы
инерции направлены по оси Оу.
и находиться в прямолин. положении
равновесия в момент врем.t=0.Точкам
струны сообщ. начальн. скорость и
отклонение. Выведем ур-ние малых
поперечных колебаний струны при t>0,если
концы струны:a)закреплены
жёстка,б)свободно, в)закреплены
упруго,г)двигаються в поперечном
направлении по заданным законам .Пусть
Ох совпадает с направл. струны в положении
равновесия. Силы натяжения и силы
инерции направлены по оси Оу.
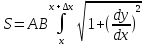 dx
dx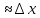 .Значит
удлинение участков струны не происходит,
след. по з.Гука сила натяжения
.Значит
удлинение участков струны не происходит,
след. по з.Гука сила натяжения
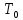 не зависит от времени ни отx.
не зависит от времени ни отx. =
=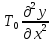 (x,t)
(x,t)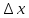 .
Пустьp(x,t)-непрерыв.
линейная плотность внешних сил, тогда
на участок АВ вдоль Оу действует сила
p(x,t)
.
Пустьp(x,t)-непрерыв.
линейная плотность внешних сил, тогда
на участок АВ вдоль Оу действует сила
p(x,t)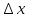 .Момент
инерции:-m
.Момент
инерции:-m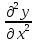 ,m-масса
участка;m=
,m-масса
участка;m=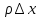 ,-
,-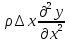 –проекция
всех сил на ось Оy.
–проекция
всех сил на ось Оy.
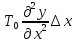 +p(x,t)-
+p(x,t)-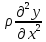 =0-ур-ние
вынужденных колебаний струны. Если
=0-ур-ние
вынужденных колебаний струны. Если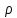 =соst,то
=соst,то
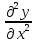 =
=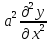 +f(x,t),где
+f(x,t),где
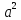 =
=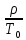 ,
,
f(x,t)=-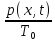 .
Кроме того ф-ция удовлетворяет начальн.
условиямa)y
.
Кроме того ф-ция удовлетворяет начальн.
условиямa)y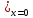 =0;y
=0;y =0;б)
=0;б)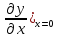 =0;
=0;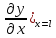 =0;
в)(
=0;
в)(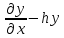 )
)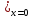 =0;
(
=0;
(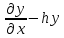 )
)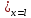 =0,h=
=0,h=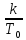 ,k-коэф.
упругости;г) y
,k-коэф.
упругости;г) y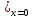 =
=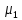 (t);
y
(t);
y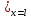 =
=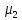 (t).
(t).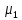 (t),
(t),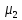 (t)-определяют
закон движения концов струны.
(t)-определяют
закон движения концов струны.
37-2.
Ур-ние
теплопроводности.Рассмотрим
в пространстве
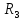 ,
декартов системы координат
,
декартов системы координат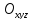 ,твёрдое телоV
и пусть температура этого тела в любой
точке этого тела в момент t
опред. U(x,y,z,t),тогда
производные
,твёрдое телоV
и пусть температура этого тела в любой
точке этого тела в момент t
опред. U(x,y,z,t),тогда
производные
 ,
,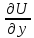 ,
,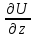 характер. скорость изменения температ.
в момент времениt
в направлении осей
характер. скорость изменения температ.
в момент времениt
в направлении осей
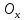 ,
,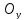 ,
,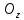 .Предпологаем,
что тепл.cв-ва
тела V
не зависят от направления.
.Предпологаем,
что тепл.cв-ва
тела V
не зависят от направления.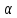 -коэф.
теплопроводности-const;C-удельная
теплоёмкость—const.
Кол-во теплоты проход. через переднюю
грань кубика в положении оси Оx
за время
-коэф.
теплопроводности-const;C-удельная
теплоёмкость—const.
Кол-во теплоты проход. через переднюю
грань кубика в положении оси Оx
за время
 равно
равно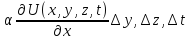 ,через
заднюю грань
,через
заднюю грань t
t
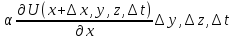 .
Тогда
.
Тогда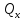 =
=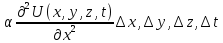 ;
;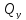 =
=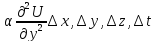 ;
;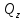 =
=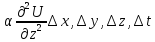 ;
тогда общее кол-во теплоты
;
тогда общее кол-во теплоты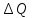 =
=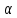 (
( )
)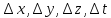 .C
другой стороны кол-во теплоты равно
произвед С и
.C
другой стороны кол-во теплоты равно
произвед С и
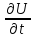 -скорость
измен. времени.
-скорость
измен. времени.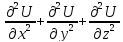 =
=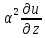 (2),
(2),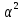 =
= ,
,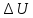 =
=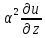 .Ур-ние
(2) получ. при условии,что внутри тела
отсутствуют тепловые источники.Если
плотность тепловых источников равнаF(x,y,z,t)
то ур-ние (2) примет вид
.Ур-ние
(2) получ. при условии,что внутри тела
отсутствуют тепловые источники.Если
плотность тепловых источников равнаF(x,y,z,t)
то ур-ние (2) примет вид
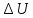 =
=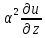 +f(x,y,z,t)(3).
Граничные условия для ур-ния (2-3) могут
быть заданы в виде: 1)U
+f(x,y,z,t)(3).
Граничные условия для ур-ния (2-3) могут
быть заданы в виде: 1)U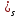 =f(s,t)
значение U
на границе s-области,
где f(s,t)
–неизвест. ф-ция своих аргументов
s-площадь
поверх. этого тела. ?2)
=f(s,t)
значение U
на границе s-области,
где f(s,t)
–неизвест. ф-ция своих аргументов
s-площадь
поверх. этого тела. ?2)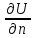
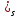 =F(s,t)
,u(x,y,z,t)
=F(s,t)
,u(x,y,z,t)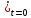 =
=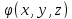 -некот.
извест. ф-ция.
-некот.
извест. ф-ция.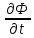 =
=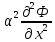 -ур-ние
диффузии ; Ф(x,t)-концентрация
раст-ра
-ур-ние
диффузии ; Ф(x,t)-концентрация
раст-ра
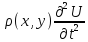 =T(
=T(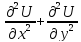 )+P(x,y,t)-ур-ние
поперечных колебаний мембраны,
)+P(x,y,t)-ур-ние
поперечных колебаний мембраны, -плотность,Т-сила
натяжения,P(x,y,t)-внешняя
сила.
-плотность,Т-сила
натяжения,P(x,y,t)-внешняя
сила.
38.Метод
реш. ур-ний мат. физики.Метод Д'Аламбера
для колебаний струны.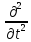 =
=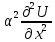 (1),-
(1),-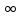 <x<
<x<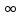 ,t>0
,t>0
начальн.условия
U(x,0)=f(x)
(2);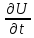 (x,0)=F(x)(3).
Найдём для (1) ур-ние характеристик
(x,0)=F(x)(3).
Найдём для (1) ур-ние характеристик
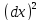 -
-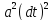 =0,dx
=0,dx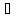 adt=0,
adt=0,
x+at=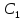 ,x-at=
,x-at=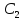 .В
(1) выполним замену
.В
(1) выполним замену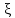 =x+at,η=x-at.
=x+at,η=x-at.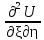 =0.Решением
этого ур-ния будет ф-цияu(
=0.Решением
этого ур-ния будет ф-цияu(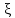 ,η)=
,η)= (
(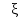 )+
)+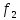 (η)
(η)
,
где
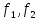 -производ.
Дважды непрерыв. диф ф-ции.Из начальн.
условийu(x,0)=f(x)=
-производ.
Дважды непрерыв. диф ф-ции.Из начальн.
условийu(x,0)=f(x)=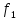 (
(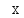 )+
)+ (x)
(*),
(x)
(*),
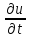 (x,0)=a
(x,0)=a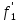 (x)-
a
(x)-
a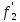 (x)
из (3) следует a
(x)
из (3) следует a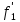 (x)-
a
(x)-
a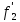 (x)=F(x).
Значит a
(x)=F(x).
Значит a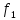 -
a
-
a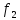 =
=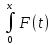 dt
(**).(*)и(**) относительно ф-ции
dt
(**).(*)и(**) относительно ф-ции
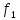 и
и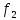 ,
получ. что
,
получ. что
Искомое
решение ур-ния (1) имеет вид u(x,t)= +
+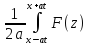 dz(4)
ф-ла Д’Аламбера для бесконечной струны.
dz(4)
ф-ла Д’Аламбера для бесконечной струны.
39.Метод
Фурье решение волнового ур-ния.Задача
Штурма-Лиувилля.Рассмотрим
задачу колеб. Конечной струны закреплённой
в точках x=0,x=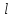 ,
состоящ. В решении ур-ния
,
состоящ. В решении ур-ния =
=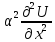 (1) -
(1) -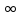 <x<
<x<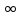 ,t>0
при начальных условиях u(x,0)=f(x);
,t>0
при начальных условиях u(x,0)=f(x);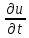 (x,0)=F(x)(2)
и граничных условиях u(0,t)=u(l,t)=0
(3). Решение (1) ищется в виде u(x,t)=X(x)T(t)
(4), где X(x)
(x,0)=F(x)(2)
и граничных условиях u(0,t)=u(l,t)=0
(3). Решение (1) ищется в виде u(x,t)=X(x)T(t)
(4), где X(x)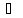 0,T(t)
0,T(t)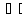 0
дважды диф. ф-ции. Подставим (4) в (1)X(x)
0
дважды диф. ф-ции. Подставим (4) в (1)X(x)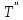 (t)=
(t)=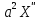 (x)T(t).
(x)T(t).
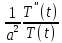 =
=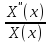 =-λ=const,зн.
Что
=-λ=const,зн.
Что
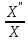 -constпри
x
-constпри
x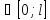 и
и
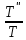 -constдля
-constдля
 t
t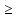 0.Получаем
сист. обыкн. диф. ур-ний
0.Получаем
сист. обыкн. диф. ур-ний
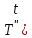 )+
)+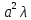 T(t)=0
и
T(t)=0
и
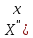 )+
)+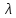 X(x)=0
(5).
X(x)=0
(5).
Из
(6) получаем X(0)T(t)=0;
X(𝑙)T(t)=0,T(t)≢0 X(0)=X(
X(0)=X(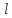 )=0,
тогда ф-цияX
явл. Решением задачи
)=0,
тогда ф-цияX
явл. Решением задачи
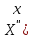 )+λX(x)=0,X(0)=X(𝑙)
(6)-(краевая задача)задача Штурма-Лиувилля,
λ-собственн. знач. этой ф-ции. X(x)-собст.
ф-ция.
)+λX(x)=0,X(0)=X(𝑙)
(6)-(краевая задача)задача Штурма-Лиувилля,
λ-собственн. знач. этой ф-ции. X(x)-собст.
ф-ция.
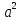 +λ=0,
+λ=0,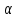 =
=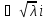 ,если
,если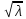 =
=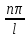 ,гдеn-натур.
число, то ненулев. решение (6) будут
,гдеn-натур.
число, то ненулев. решение (6) будут
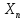 (x)=
(x)=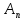 sin
sin x,
где n-натур.
число. (7) λ =
x,
где n-натур.
число. (7) λ =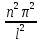 ,
тогда общее решение
,
тогда общее решение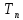 (t)=
(t)=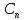 cos
cos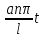 +
+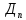 sin
sin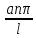 ;
;
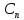 ,
, -
константы. Согласно (4)
-
константы. Согласно (4)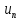 (x,t)=
(x,t)=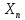 (x)
(x)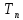 (t)
будет частичным решением ур-нием (1). А
общее решение u(x,t)=
(t)
будет частичным решением ур-нием (1). А
общее решение u(x,t)=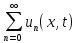 =
=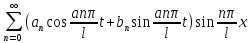 (8),
(8),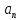 =
=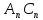 ,
,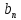 =
=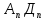 ;
из нач. условий (2) следует
;
из нач. условий (2) следует
u(x,0)=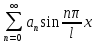 =f(x);
=f(x);
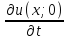 =
=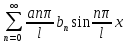 =F(x);
из (8)
=F(x);
из (8)
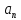 =
=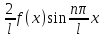 dx;
dx;
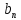 =
=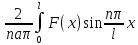 dx;
(9), Подставив (9) в (8), получим решение (1)
удовл. услов. (2) и (3)
dx;
(9), Подставив (9) в (8), получим решение (1)
удовл. услов. (2) и (3)
40.Решение
задачи Дирихре для ур-ния Лапласа в
круге методом Фурье.
Ур-ние теплопровод. в стационар. случае
имеет вид
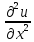 +
+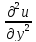 +
+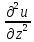 =0
(1 ) однород. ур-ние Лапласа;
=0
(1 ) однород. ур-ние Лапласа; u=0
–оператор. форма. Для задач относящихся
к плоским фигурам ур-ние имеет вид
u=0
–оператор. форма. Для задач относящихся
к плоским фигурам ур-ние имеет вид
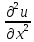 +
+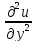 =0
(2); Задача Дирихле для ур. Лапласа состоит
в том, чтобы найти ф-циюu=u(x,y)
удовлет. (2) и гранич. услов.: u
=0
(2); Задача Дирихле для ур. Лапласа состоит
в том, чтобы найти ф-циюu=u(x,y)
удовлет. (2) и гранич. услов.: u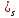 =f(x,y)
(3). Введём поляр. сист. координат:
x=
=f(x,y)
(3). Введём поляр. сист. координат:
x=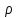 cos
cos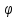 ,y=
,y=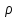 sin
sin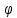 ,
0
,
0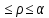 ,
0
,
0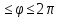 тогда (2) запишеться в виде
тогда (2) запишеться в виде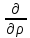 (
(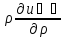 )+
)+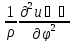 =0
(4) гдеũ(
=0
(4) гдеũ(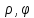 )=u(
)=u(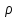 cos
cos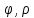 sin
sin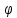 ).
Решение (4) ищем ũ(
).
Решение (4) ищем ũ( )=R(
)=R(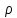 )Ф(
)Ф(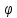 ).
Подставляем посл. равенство в (4) получим
).
Подставляем посл. равенство в (4) получим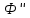 +λФ=0;
Ф≢0
и
+λФ=0;
Ф≢0
и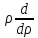 (
(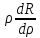 )-λR=0,R≢0
тогда ф-ция
)-λR=0,R≢0
тогда ф-ция
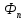 (
(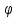 )=
)=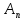 cos
cos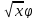 +
+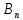 sin
sin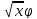 -
общее решение диф. ур-ния относит. Ф(
-
общее решение диф. ур-ния относит. Ф(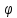 ),
где А и Вconst,
ф-ция ũ(
),
где А и Вconst,
ф-ция ũ(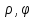 )
явл. ф-ция 2
)
явл. ф-ция 2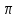 -период.
То
-период.
То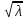 =n,
n=0,1,2…
следовательно
=n,
n=0,1,2…
следовательно
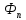 (
(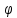 )=
)=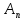 cos
cos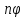 +
+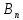 sin
sin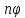 .
Диф ур-ния относ. ф-ции R(
.
Диф ур-ния относ. ф-ции R(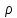 )
имеет общее решение вида
)
имеет общее решение вида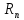 (
(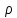 )=
)=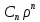 +
+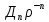 ,
где
,
где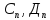 -const.
Так как ũ(
-const.
Так как ũ(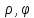 )
удовлет. ур. Лапласа следова. явл.
гармонич. и непрерыв. в круге 0
)
удовлет. ур. Лапласа следова. явл.
гармонич. и непрерыв. в круге 0 ,
0
,
0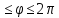 .
Согласно теореме Вейерштрасса эта
ф-ция ограничена в круге , зн. Необходимо
полож. Что
.
Согласно теореме Вейерштрасса эта
ф-ция ограничена в круге , зн. Необходимо
полож. Что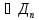 =0,
дляn=0,1,2….
Значит част. реш. ур-ния (4) задачи Дирихре
для круга явл. ф-ция
=0,
дляn=0,1,2….
Значит част. реш. ур-ния (4) задачи Дирихре
для круга явл. ф-ция
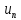 (
(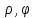 )=
)=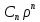 (
(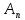 cos
cos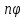 +
+ sin
sin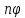 )=
)=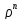 (
(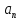 cos
cos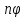 +
+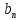 sin
sin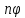 ).
ũ(
).
ũ(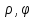 )=
)=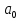 +
+ (5) –общее решение.Чтобы опред. коэф.
(5) –общее решение.Чтобы опред. коэф.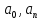 ,
, использ. нач. условиеũ
использ. нач. условиеũ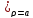 =f̃(
=f̃(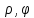 )
)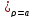 =f̃(
=f̃(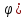 .Тогда
решение задачи Дирихле :ũ(
.Тогда
решение задачи Дирихле :ũ( )=
)=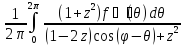 гдеz=
гдеz=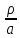
41.Метод
сеток для решения ур-ний математической
физики:
задача решения диф. ур-ния в частных
производных с непрерывной обл. изменению
аргументов и краевыми условиями подменяем
другой задачей, вместо непрер. обл.
изменения аргументов рассматривается
дискретная обл. Решен. ур. с двумя
переменными: будем считать x,y
декартов. ортогон. координ. точки на
плоскости.Покроем эту плоскость сеткой
x=mh,
y=nh;
m,n=0, , гдеh-заданное
положит. число. Узел-вершина каждого
квадрата полученной сетки, шаг-число
h.
В каждом узле (x,y)
при условии, что все шесть точек
(x,y),(x-h,y),(x+h,y),(x,y-h),(x,y+h),(x+h,y+h)
, гдеh-заданное
положит. число. Узел-вершина каждого
квадрата полученной сетки, шаг-число
h.
В каждом узле (x,y)
при условии, что все шесть точек
(x,y),(x-h,y),(x+h,y),(x,y-h),(x,y+h),(x+h,y+h) облD
ф-ции u(x,y),
дважды непрер. диф. в D.
облD
ф-ции u(x,y),
дважды непрер. диф. в D.
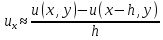 ,
,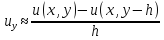 ,
,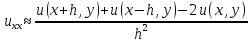 ;
;
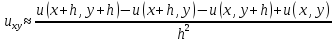 ;
;
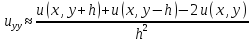 ;
a(x,y)
;
a(x,y)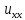 +2b(x,y)
+2b(x,y)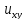 +
c(x,y)
+
c(x,y)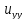 +d(x,y)
+d(x,y)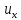 +l(x,y)
+l(x,y)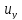 +f(x,y)u=g(x,y).Решение
ур. теплопров. методом сеток:
+f(x,y)u=g(x,y).Решение
ур. теплопров. методом сеток: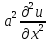 =
=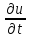 (1),u=u(x,y)-искомая
ф-ция определяет распределение температуры
в люб. точке x
стержня длиной l
в люб. момент времени t.
Начальн. условия u(x,0)=f(x),
краевые условия u(0,t)=
(1),u=u(x,y)-искомая
ф-ция определяет распределение температуры
в люб. точке x
стержня длиной l
в люб. момент времени t.
Начальн. условия u(x,0)=f(x),
краевые условия u(0,t)=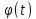 ,u(l,t)=
,u(l,t)= (t);
f(x),
(t);
f(x), -непрерыв.
ф-ции. Сист. координатOxt
и в области 0
-непрерыв.
ф-ции. Сист. координатOxt
и в области 0 x
x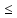 l,
t
l,
t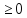 .
.
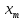 =mh,
=mh,
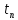 =n
=n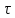 ,
,
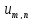 =u(
=u(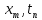 ).
Аппроксимируем ур. (1)L(u)=
).
Аппроксимируем ур. (1)L(u)=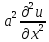 --
--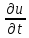 =0(2)
конечно-разностным
=0(2)
конечно-разностным =
=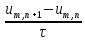 , преобазуем
, преобазуем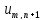 =
=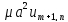 +(1-2
+(1-2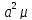 )
)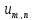 +
+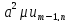 (3) , где
(3) , где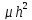 =
=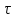 ,
,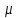 -положит.
числов. множитель.L(u)-
-положит.
числов. множитель.L(u)-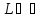 (u)=R(u)(4)-ошибка
аппроксимации ,выберем
(u)=R(u)(4)-ошибка
аппроксимации ,выберем
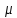 =
=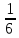 ,L͞(u)=
,L͞(u)=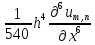 +O(
+O(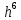 )
(5), подставим
)
(5), подставим в (3)
в (3)
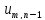 =
=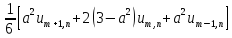 (6)
(6) (
(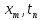 )=
)=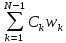 (
(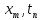 )=
)=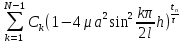 sin
sin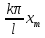
конечно-разностная
схема будет устойчивой при любых
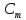 если ф-цияw(
если ф-цияw(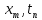 )
останетс ограниченной приt
)
останетс ограниченной приt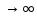 ,достаточно
, чтобы при всех k
выполн. Неравенство |1-4
,достаточно
, чтобы при всех k
выполн. Неравенство |1-4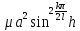 |
|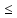 1,
0
1,
0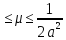 –определяет достаточное условие
устойчивости.
–определяет достаточное условие
устойчивости.
