- •1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- •2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
- •2.Однородные ду
- •5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
- •8.Линейная зависимость,независимость ф-ий. Определитель вронского.
- •9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
- •12Линейные однородные системы ду высших порядков с постоянными коэффициентами
- •13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
- •15 Устойчивость по Ляпунову
- •16 Устойчивость по первому приближению
- •19.Предел и непрерывность функций комплексной переменной.
- •22.Элеменарные функции комплексной переменной.
- •25.Теорема Коши и интегральная формула Коши.
- •26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
- •27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
- •28. Нули аналитических функций. И их классификация.
- •29. Ряд Лорана. Изолированные особые точки и их классификация.
- •32. Вычет аналитических функций.
- •35.Классификац.Ур. Матфизики.
- •42. Оригинал и изображение. Св-ва преобразования Лапласа: линейность, подобие.
- •44. Формулы обращения преобразования Лапласа.
- •45. Применение преобразования Лапласа: теоремы обращения.
- •46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
- •47. Применение преобразования Лапласа к решению физических задач.
- •48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
2.Однородные ду
Ф-я
P(xy)
наз. однородной ф-ей степени m,
если
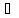 t
t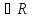 она удовлетворяет равенству:
P(tx,ty)=
она удовлетворяет равенству:
P(tx,ty)=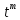 P(xy).
Ур-е вида(1) наз. однородным, если входящие
в него ф-ии P(xy),
Q(xy)-однородные
ф-ии одной степени.Ур-е (1) можно решить
при помощи замены y=ux,
u-неизвестная
ф-я, x-аргумент.
P(xy).
Ур-е вида(1) наз. однородным, если входящие
в него ф-ии P(xy),
Q(xy)-однородные
ф-ии одной степени.Ур-е (1) можно решить
при помощи замены y=ux,
u-неизвестная
ф-я, x-аргумент.
P(tx,ty)=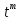 P(xy);
t=
P(xy);
t=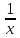 ;P(1,
;P(1,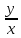 )=
)=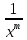 P(xy);
Q(1,
P(xy);
Q(1,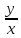 )=
)=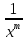 Q(xy);
Q(xy);
P(xy)=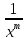 P(1,
P(1,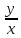 );
Q(xy)=
);
Q(xy)=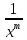 Q(1,
Q(1,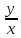 )
)
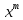 P(1,
P(1,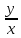 )dx+
)dx+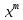 Q(1,
Q(1,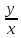 )dy=0;
)dy=0;
P(1,u)dx+Q(1,u)dy=0; dy=xdu+udx;
P(1,u)dx+Q(1,u)(xdu+udx)=0; (P(1,u)+uQ(1,u))dx+xQ(1,u)du=0
Ln(x)+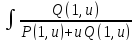 du=C;
u=
du=C;
u=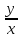 ;
;
К
однородным ур-ям приводятся также
уравнения вида: y’=f(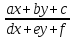 );Замена
переменной:
);Замена
переменной:
x=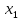 +
+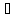 ;
y=
;
y=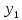 +
+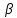 ;
y’(x)=
;
y’(x)=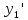 (x);
(x); (x)=f(
(x)=f(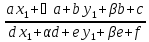 );
);
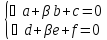 ;
Находим
;
Находим
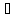 и
и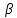 ,и
сводим к однородному.
,и
сводим к однородному.
4-1. ДУ 1-го порядка,интегрируемые в квадратурах.
1.
Линейные уравнения.
Ур-е вида(1): y’+p(x)y=q(x)
и (1’):x’+p(y)x=q(x),
гдеp
и q
непрерывны на некот. интервале(a,b),называются
линейными относительно y
и x.
Если q(x)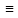 0
(q(y)
0
(q(y)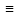 0),
то(1) ((1’)) называется однородным ,еслиq(x)
0),
то(1) ((1’)) называется однородным ,еслиq(x) 0
(q(y)
0
(q(y)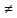 0),
то (1) ((1’)) наз.линейным неоднородным.
0),
то (1) ((1’)) наз.линейным неоднородным.
y’+p(x)y=0;
 +p(x)y=0;
+p(x)y=0;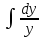 +
+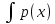 dx=
dx=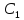 ;
;
ln(y)+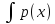 dx=lnC;
y=C
dx=lnC;
y=C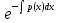 =C
=C (3);
(3);
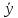 =
=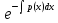 ;
Т.к.y=o
входит в решение (3),то формула(3) есть
общее решение ур-я (2).
;
Т.к.y=o
входит в решение (3),то формула(3) есть
общее решение ур-я (2).
Лин.неодн.у-е:
y’+p(x)y=q(x);
При этом решение у-я(1) будем искать в
виде(4): y=C(x)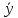 ,
где
,
где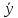 =
=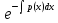 ;C(x)-некоторая
неизв.ф-я. Подставим (4) в (1):
;C(x)-некоторая
неизв.ф-я. Подставим (4) в (1):
(C(x)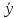 )’+p(x)(C(x)
)’+p(x)(C(x)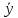 )=q(x)
)=q(x)
C’(x)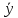 +C(x)
+C(x) ’+p(x)C(x)
’+p(x)C(x) =q(x);
=q(x);
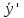 =
=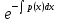 (-p(x))=
(-p(x))=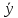 (-p(x));
(-p(x));
C’(x)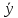 -C(x)
-C(x)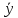 p(x)+p(x)C(x)
p(x)+p(x)C(x) =q(x);
=q(x);
C’(x)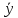 =q(x);
=q(x);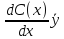 =q(x);
dC(x)=
=q(x);
dC(x)=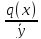 dx;
dx;
C(x)=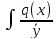 dx+C;
Подставляя найденное C(x)
в (4) получим формулу Бернулли:
dx+C;
Подставляя найденное C(x)
в (4) получим формулу Бернулли:
y=C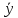 +
+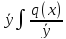 dx;Описанный
метод решения ур-я (1) называют методом
вариации произвольной постоянной или
или метод Лагранжа. Другим методом
решенияу-я (1) явл. метод Бернулли. В (1)
делают замену y=UV,U=U(x),
V=V(x)-непрерывно
диф-мые на (ab)
ф-ии, причём U(x)
dx;Описанный
метод решения ур-я (1) называют методом
вариации произвольной постоянной или
или метод Лагранжа. Другим методом
решенияу-я (1) явл. метод Бернулли. В (1)
делают замену y=UV,U=U(x),
V=V(x)-непрерывно
диф-мые на (ab)
ф-ии, причём U(x)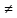 0,V(x)
0,V(x)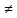 0.
После подстановкиy
(1) получим:
0.
После подстановкиy
(1) получим:
(UV)’+p(x)UV=q(x); U’V+UV’+p(x)UV=q(x);
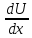 V+U(
V+U(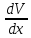 +p(x)V)=q(x)
(5); Требуем, чтобы :
+p(x)V)=q(x)
(5); Требуем, чтобы :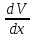 +p(x)V=0
и ищем частное решение этого ур-я.
+p(x)V=0
и ищем частное решение этого ур-я.
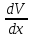 +p(x)V=0;
lnV=-
+p(x)V=0;
lnV=-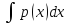 +lnC;
lnC=0;
+lnC;
lnC=0;
V=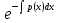 ;
подставляя это решение в (5)получаем:
;
подставляя это решение в (5)получаем: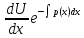 =q(x);dU
=q(x);dU =q(x)dx;
домнажаем на
=q(x)dx;
домнажаем на
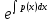 ,
,
dU=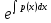 q(x)dx,
откуда: U=
q(x)dx,
откуда: U=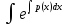 q(x)dx+C,
окончательное общее решение у-я (1)
принимает вид:
q(x)dx+C,
окончательное общее решение у-я (1)
принимает вид:
y=C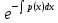 +
+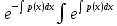 q(x)dx.
q(x)dx.
4-2.
2.Ур-ем
Бернулли-
наз.нелинейное ДУ 1-го порядка вида(1):
y’+p(x)y=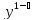 q(x),
где
q(x),
где
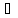 -
любое действ.число
-
любое действ.число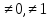 .
Ур-е (1) можно свести к линейному при
помощи заменыU=
.
Ур-е (1) можно свести к линейному при
помощи заменыU=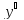 ,
либо решать его при помоши подстановкиy=U(x)V(x),
тогда получаем(2):
,
либо решать его при помоши подстановкиy=U(x)V(x),
тогда получаем(2):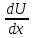 V+U(
V+U(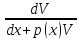 )=
)=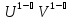 q(x);
Далее ищем частное решение ур-я:
q(x);
Далее ищем частное решение ур-я:
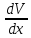 +p(x)V=0;
(V=V(x)),
подставляя которое в (2) получаем ур-е с
разделяющимися перемпнными для нахождения
неизвестной ф-ии U.
Подставляя найденные U(x)
и V(x)
в y=UV,получаем
общее решение у-я (1).
+p(x)V=0;
(V=V(x)),
подставляя которое в (2) получаем ур-е с
разделяющимися перемпнными для нахождения
неизвестной ф-ии U.
Подставляя найденные U(x)
и V(x)
в y=UV,получаем
общее решение у-я (1).
3.Уравнения
в полных дифференциалах. Ур-е
вида(1): P(xy)dx+Q(xy)dy=0;наз.
ур-ем полных диф-лов, если его левая
часть является полным диф-лом некот.
ф-ии U:
P(xy)dx+Q(xy)dy=U;
U=U(xy);
Если ф-ии P,
Q,
 ,
,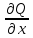 непрерывны в некот.односвязной областиD
непрерывны в некот.односвязной областиD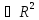 ,
тоусловие ,
,
тоусловие ,
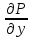 =
=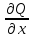 является необходимым и достаточным для
того, чтобы выражение (Pdx+Qdy)
было полным диф-лом ф-ии U.
является необходимым и достаточным для
того, чтобы выражение (Pdx+Qdy)
было полным диф-лом ф-ии U.
1)P(xy)=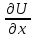 ;
Q(xy)=
;
Q(xy)=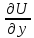 ;
;
2)U=U(xy)=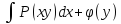 ;
;
3)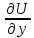 =(
=(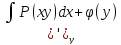 =Q(xy)
=Q(xy)
4)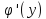 =f(y);
=f(y);
5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
ДУ
n-ого
порядка наз. у-е вида:F(x,y,y’,y’’,…,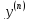 )=0.
Зушением такого ур-я служит всякое n
раз непрерыв.диф-мая ф-я y=
)=0.
Зушением такого ур-я служит всякое n
раз непрерыв.диф-мая ф-я y=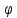 (x)
определённая на (ab)
и обращающая данное у-е в верное тождество.
F(x,
(x)
определённая на (ab)
и обращающая данное у-е в верное тождество.
F(x,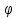 (x),
(x),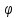 ’(x),…,
’(x),…,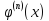 )
)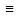 0.
Задача Коши для у-яn-ого
порядка заключ. В том, чтобы найти решение
у-я удовл. условию (1):y=
0.
Задача Коши для у-яn-ого
порядка заключ. В том, чтобы найти решение
у-я удовл. условию (1):y=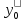 ;y’=
;y’=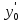 ;
;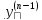 =
=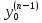 ;
приx=
;
приx=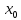 ,
где
,
где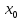 ,
,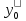 ,
,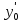 …-заданные
числа,кот. наз.начальными условиями.
…-заданные
числа,кот. наз.начальными условиями.
Ф-я
y=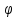 (x,
(x, ,
,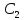 ,…,
,…,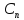 )
наз. общим решением ДУn-ого
порядка в области единственности решения
зад.Коши, если она удовлетворяет этому
условию при любых значениях произв.
постоянных
)
наз. общим решением ДУn-ого
порядка в области единственности решения
зад.Коши, если она удовлетворяет этому
условию при любых значениях произв.
постоянных
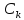 ,k=
,k=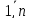 и каковы бы нибыли нач. усл. (1) всегда
можно подобрать числа
и каковы бы нибыли нач. усл. (1) всегда
можно подобрать числа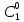 ,
,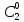 ,…,
,…,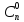 ,
которые будут удовлетворять нач.усл.
(1).
,
которые будут удовлетворять нач.усл.
(1).
Всякое
решение, которое получается из общего
при конкретных значениях переменных
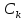 наз. частным решением этого уравнения.
Уравнение может иметь частные решения
,кот. не получаются из общего решения(особые).
Выражение вида Ф(x,y,
наз. частным решением этого уравнения.
Уравнение может иметь частные решения
,кот. не получаются из общего решения(особые).
Выражение вида Ф(x,y,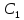 ,
,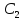 ,…,
,…,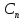 )=0,
определяющее общее решение как неявную
ф-ю наз. общим ин-лом ДУ. Ур-еn-ого
порядка, разрешённое относительно
старшей производной имеет вид (2):
)=0,
определяющее общее решение как неявную
ф-ю наз. общим ин-лом ДУ. Ур-еn-ого
порядка, разрешённое относительно
старшей производной имеет вид (2):
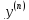 =f(x,y,y’,…,
=f(x,y,y’,…,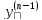 );Теорема
сущ. и единст.реш.зад.Коши: Если
в (2) ф-я f(x,y,y’,…,
);Теорема
сущ. и единст.реш.зад.Коши: Если
в (2) ф-я f(x,y,y’,…,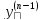 )
в некоторой областиD
непрерывна и имеет непрерывные частные
производные
)
в некоторой областиD
непрерывна и имеет непрерывные частные
производные
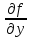 ;
;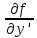 ;
;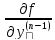 то для любой точки (
то для любой точки (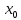 ,
,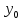 ,
, ,…,
,…,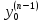 )
)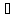 D
существует такой интервал
D
существует такой интервал
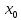 -h<x<
-h<x<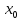 +h,
на котором существует притом единственное
решение уравнения(2),удовл. усл.(1).
+h,
на котором существует притом единственное
решение уравнения(2),удовл. усл.(1).
6.ДУ n-ого порядка,допускающие понижение порядка.
Интегрирование у-я n-ого порядка удаётся только в некоторых частных случаях. Рассмотрим у-е допускающее понижение порядка:
1)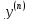 =f(x);
Решение этого у-я находится n-кратным
интегрированием:
=f(x);
Решение этого у-я находится n-кратным
интегрированием:
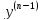 =
=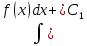 =
=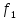 (x)+
(x)+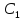 ;
;
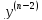 =
=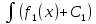 dx=
dx=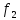 (x)+
(x)+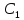 x+
x+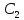 ;
;
Y=y(x)=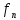 (x)+
(x)+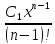 +
+ +
+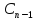 x+
x+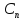 ;
;
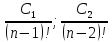 —произвольные
постоянные величины.
—произвольные
постоянные величины.
Общее решение может быть записано в виде:
Y=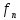 (x)+
(x)+ +
+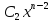 +…+
+…+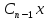 +
+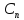 ;
;
2)У-я
вида: F(x,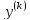 ,…,
,…,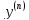 )=0
– у-я несодержащие искомой ф-иy
и её производные до порядка k-1
включительно. С помощью замены
)=0
– у-я несодержащие искомой ф-иy
и её производные до порядка k-1
включительно. С помощью замены
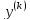 =z(x),
порядок этого у-я понижается на k
единиц.
=z(x),
порядок этого у-я понижается на k
единиц.
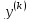 =z(x)
: F(x,z,…,
=z(x)
: F(x,z,…,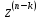 )=0;
Если можно найти общее решение этого
у-яz=
)=0;
Если можно найти общее решение этого
у-яz=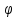 (x,
(x,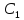 ,…,
,…,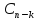 ),
то искомая ф-яy(x)
получается путём k-кратного
интегр. ф-и
),
то искомая ф-яy(x)
получается путём k-кратного
интегр. ф-и
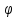 (x,
(x,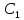 ,…,
,…,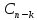 ).
).
3)У-е
вида F(y,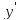 ,…,
,…,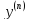 )=0
– это у-е ,которое явно не содержит
независимой переменной, тогда подстановкойy
’=z(y),
порядок этого уравнения уменьшается
на единицу.
)=0
– это у-е ,которое явно не содержит
независимой переменной, тогда подстановкойy
’=z(y),
порядок этого уравнения уменьшается
на единицу.
4)У-я
вида
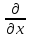 (Ф(x,y,y
’,
(Ф(x,y,y
’,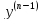 )=0
– это у-е, у которого левая часть может
быть представлена как полная производная
по х некот. ф-ии Ф. Если это уравнение
проинтегрировать по х, то получается
у-е, порядок кот.на единицу меньше
исходного.
)=0
– это у-е, у которого левая часть может
быть представлена как полная производная
по х некот. ф-ии Ф. Если это уравнение
проинтегрировать по х, то получается
у-е, порядок кот.на единицу меньше
исходного.
5)У-е
вида F(x,y,y
’,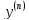 )=0,
гдеF-однородн.ф-я
относительно y
и её производных. Подстановкой y
‘=zy
порядок у-я уменьшается на единицу.
)=0,
гдеF-однородн.ф-я
относительно y
и её производных. Подстановкой y
‘=zy
порядок у-я уменьшается на единицу.
7.Линейное
ДУ n-го
порядка
– ур-ие вида
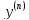 +
+
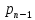 (x)
(x)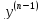 +
… +
+
… +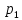 (x)y’
+
(x)y’
+
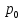 y
= f(x)
(*),
где
y
= f(x)
(*),
где
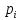 (x),
(x),
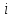 =
=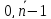 иf(x)
непрерывны
на (a,b). Линейный
див. оператор n-го
порядка
выражение вида
иf(x)
непрерывны
на (a,b). Линейный
див. оператор n-го
порядка
выражение вида
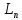 =
=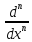 +
+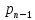 (x)
(x)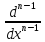 +… +
+… + (x)
(x)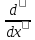 +
+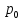 (x).
Свойства
(x).
Свойства
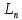 [y]
= f(x):
а)однородности:
[y]
= f(x):
а)однородности:
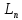 [cy]
= c
[cy]
= c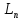 [y]
б)аддитивность:
[y]
б)аддитивность:
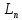 [
[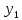 +
+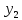 ]
=
]
= [
[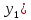 +
+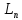 [
[ ].
].
Ур-е
(*) наз. Линейным неоднородным, если f(x)
≠ 0, если f(x)
≡
0, т.е.
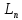 [y]
= 0, то его называют- лин. однродным. Задача
Коши:
найти решения (*) удлетвор. условиям y(
[y]
= 0, то его называют- лин. однродным. Задача
Коши:
найти решения (*) удлетвор. условиям y(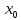 )
=
)
=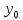 ,y`(
,y`(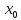 )
=
)
=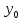 ’,…,
’,…,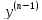 (
(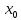 )
=
)
= (**)- начальные условия.
(**)- начальные условия.
Общее
решение ур-я (*)
– ф-ия y
=
 (x,
(x,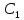 ,…,
,…,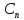 ),
зависящая от n и удлетворяющая условиям:
),
зависящая от n и удлетворяющая условиям:
при любых
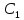 ,…,
,…,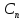 ф-ия y
=
ф-ия y
=
 (x,
(x,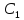 ,…,
,…,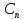 )
явл.
решением (*).
)
явл.
решением (*).для любых (**) можно подобрать
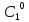 ,…,
,…,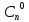 постоянных
постоянных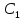 ,…,
,…,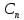 ,
что y
=
,
что y
=
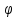 (x,
(x, ,…,
,…,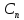 )
будет удовлетворять(**).
)
будет удовлетворять(**).
Свойства лин. однор. урав.:
если ф-ции
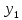 ,
,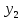 ,…,
,…,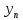 линейно зависемы на (a,b), то определитель
Вронского равен 0 на (a,b).
линейно зависемы на (a,b), то определитель
Вронского равен 0 на (a,b).если опред. Вронского ≠ 0 при x =
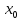
 (a,b),
составленный для решений
(a,b),
составленный для решений
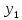 ,
,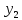 ДУy’’+py’+qy=0,
то он ≠
0
ни при одном x из (a,b).
ДУy’’+py’+qy=0,
то он ≠
0
ни при одном x из (a,b).если решения
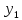 ,
,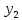 ДУy’’+py’+qy=0,
линейно независимы на (a,b), то опред
Вронского ≠
0
ни при одном x из (a,b).
ДУy’’+py’+qy=0,
линейно независимы на (a,b), то опред
Вронского ≠
0
ни при одном x из (a,b).
Структура
общ реш неоднор лин уравнения
– сумма какого-нить частного решения
y*
этого уравнения и общего решения
 соответсвующего уравнения, т.еy
= y*
+
соответсвующего уравнения, т.еy
= y*
+