
- •1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- •2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
- •2.Однородные ду
- •5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
- •8.Линейная зависимость,независимость ф-ий. Определитель вронского.
- •9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
- •12Линейные однородные системы ду высших порядков с постоянными коэффициентами
- •13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
- •15 Устойчивость по Ляпунову
- •16 Устойчивость по первому приближению
- •19.Предел и непрерывность функций комплексной переменной.
- •22.Элеменарные функции комплексной переменной.
- •25.Теорема Коши и интегральная формула Коши.
- •26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
- •27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
- •28. Нули аналитических функций. И их классификация.
- •29. Ряд Лорана. Изолированные особые точки и их классификация.
- •32. Вычет аналитических функций.
- •35.Классификац.Ур. Матфизики.
- •42. Оригинал и изображение. Св-ва преобразования Лапласа: линейность, подобие.
- •44. Формулы обращения преобразования Лапласа.
- •45. Применение преобразования Лапласа: теоремы обращения.
- •46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
- •47. Применение преобразования Лапласа к решению физических задач.
- •48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
Найдём
частное решение д.у.:
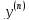 +
+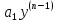 +
… +
+
… +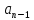 (y)’
+
(y)’
+
 y
= f(t)
– формула (1), начальные условия которого
y(0)=
y
= f(t)
– формула (1), начальные условия которого
y(0)=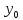 ;y
’(0) =
;y
’(0) =
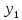 ,…,
,…,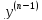 (0)
=
(0)
= ,где
,где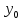 ,
,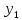 ,…,
,…,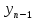 -
заданные числа. Пусть ф-яy(t),все
её производные и f(t)
являются оригиналами. Тогда y(t)
-
заданные числа. Пусть ф-яy(t),все
её производные и f(t)
являются оригиналами. Тогда y(t)
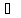 Y(p);
y’(t)
Y(p);
y’(t)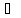 pY(p)
-
pY(p)
-
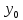 ;f(t)
;f(t)
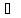 F(p).
Перейдём в (1) от оригиналов к изображениям:
F(p).
Перейдём в (1) от оригиналов к изображениям:
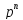 Y(p)
-
Y(p)
-
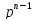
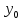 - … -
- … -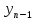 )
+
)
+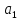 (
( Y(p)
-
Y(p)
-
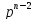
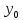 - … -
- … -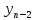 )
+…+
)
+…+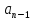 (p
Y(p)-
(p
Y(p)-
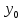 )
+
)
+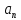 Y(p)=F(p).
Полученное ур-е называют операторным(ур-ем
в изображениях). Решаем относительно
Y(p):
Y(p)(
Y(p)=F(p).
Полученное ур-е называют операторным(ур-ем
в изображениях). Решаем относительно
Y(p):
Y(p)(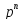 +
+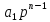 +…+
+…+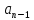 p
+
p
+ )
= F(p) +
)
= F(p) + (
(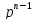 +
+ +…+
+…+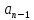 )
+
)
+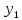 (
(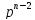 +
+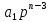 +…+
+…+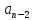 )
+…+
)
+…+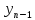 , т.е.Y(p)
, т.е.Y(p)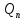 (p)
= F(p)
(p)
= F(p)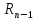 (p)
, где
(p)
, где
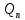 (p)
и
(p)
и
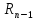 (p)
– алгебраические многочлены от p
степени n
и n
– 1, соответственно. Откуда Y(p)
= F(p)
(p)
– алгебраические многочлены от p
степени n
и n
– 1, соответственно. Откуда Y(p)
= F(p)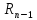 (p)/
(p)/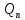 (p)
- ф-ла (2). Полученное равенство наз.
операторным
решением д.у. (1).
Если все начальные условия равны нулю,
т.е. y(0)=
y
’(0)= …=
(p)
- ф-ла (2). Полученное равенство наз.
операторным
решением д.у. (1).
Если все начальные условия равны нулю,
т.е. y(0)=
y
’(0)= …=
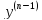 (0)
= 0, то выражение примет вид:Y(p)
= F(p)
/
(0)
= 0, то выражение примет вид:Y(p)
= F(p)
/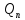 (p)
– формула (3). Находя оригинал y(t),
соответствующий изображению (2), получим
частное решение д.у. (1). Полученное
решение y(t)
во многих случаях оказывается справедливым
при всех значениях t
(а не только при t
≥ 0). Указанным методом можно найти и
общее решение д.у. (1), для этого начальные
условия запишутся в виде: y(0)=
(p)
– формула (3). Находя оригинал y(t),
соответствующий изображению (2), получим
частное решение д.у. (1). Полученное
решение y(t)
во многих случаях оказывается справедливым
при всех значениях t
(а не только при t
≥ 0). Указанным методом можно найти и
общее решение д.у. (1), для этого начальные
условия запишутся в виде: y(0)=
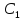 ,y
’(0)=
,y
’(0)=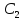 ,…,
,…, (0)
=
(0)
=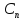 .
При решении д.у. иногда удобно использовать
формулу Дюамеля. Рассмотрим ур-е (1) при
нулевых начальных условияхy(0)=
y
’(0)= …=
.
При решении д.у. иногда удобно использовать
формулу Дюамеля. Рассмотрим ур-е (1) при
нулевых начальных условияхy(0)=
y
’(0)= …=
 (0)
= 0. Предположим, что известно решение
(0)
= 0. Предположим, что известно решение (t)
ур-ия (1) при правой части f(t)
= 1 и нулевых начальных условиях. Так как
f(t)
=1
(t)
ур-ия (1) при правой части f(t)
= 1 и нулевых начальных условиях. Так как
f(t)
=1
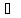 F(p)
= 1/p
, формула (3) будет
F(p)
= 1/p
, формула (3) будет
 (p)=
1/(p
(p)=
1/(p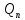 (p))
– формула (4), где
(p))
– формула (4), где
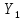 (p)
– изображение решения
(p)
– изображение решения
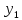 (t).
Из (3) и (4) находим Y(p)=
pF(p)
(t).
Из (3) и (4) находим Y(p)=
pF(p)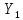 (p).
Согласно формуле Дюамеля: pF(p)
(p).
Согласно формуле Дюамеля: pF(p)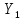 (p)
(p) f(t)
f(t) (0)
+
(0)
+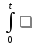 (f(τ)
(f(τ)
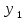 (t-τ))dτ.
Так как
(t-τ))dτ.
Так как
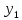 (0)=
0, тоpF(p)
(0)=
0, тоpF(p)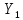 (p)
(p)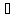
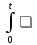 (f(τ)
(f(τ)
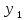 (t-τ))dτ.
Тогда решение ур-я (1) при нулевых начальных
условиях будет иметь вид: y(t)
=
(t-τ))dτ.
Тогда решение ур-я (1) при нулевых начальных
условиях будет иметь вид: y(t)
=
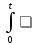 (f(τ)
(f(τ)
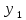 (t-τ))dτ,
где
(t-τ))dτ,
где
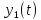 – решение ур-я (1) приf(t)
=1 и нулевых начальных условиях.
– решение ур-я (1) приf(t)
=1 и нулевых начальных условиях.
47. Применение преобразования Лапласа к решению физических задач.
Пусть
i(t),
u(t)
– ток и напряжение. Тогда I(p)
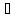 i(t);
U(p)
i(t);
U(p)
 u(t)
операторный ток и напряжение соответственно.
u(t)
операторный ток и напряжение соответственно.
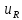 (t)
= R
i(t)
– напряжение на резисторе,
(t)
= R
i(t)
– напряжение на резисторе,
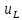 (t)
= L
d(i(t))/dt
–напряжение на катушке с индуктивностью
L.
(t)
= L
d(i(t))/dt
–напряжение на катушке с индуктивностью
L.
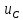 (t)
=
(t)
=

 i(τ)dτ
+
i(τ)dτ
+
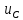 (0)
– напряжение на конденсаторе, с ёмкостью
С. Переходя к изображениям:
(0)
– напряжение на конденсаторе, с ёмкостью
С. Переходя к изображениям: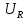 (p)
= R
I(p),
(p)
= R
I(p),
 (p)
= pLI(p)
– Li(0),
(p)
= pLI(p)
– Li(0),
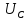 (p)
=
(p)
=
 I(p)
+
I(p)
+
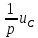 (0).
Используя закон Ома в операторной форме,
для произвольного участка цепи можно
записатьU(p)
= Z(p)
I(p),
где Z(p)
– операторное сопротивление указанного
участка цепи. Тогда для участка цепи с
R,
L,
C
при начальных условиях операторное
сопротивление имеет вид
(0).
Используя закон Ома в операторной форме,
для произвольного участка цепи можно
записатьU(p)
= Z(p)
I(p),
где Z(p)
– операторное сопротивление указанного
участка цепи. Тогда для участка цепи с
R,
L,
C
при начальных условиях операторное
сопротивление имеет вид
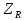 (p)=
R,
(p)=
R,
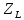 (p)
= Lp,
(p)
= Lp,
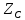 (p)=
(p)=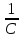 p
соответственно. При ненулевых начю
усл-ях у имеющимся в цепи источникам
э.д.с. добавляются дополнительные
источники энергии. Величины э.д.с.
дополнительных источников определяются
запасами энергии в индуктивности и
ёмкости и равно в операторном виде
соответственно Li(0)
и –
p
соответственно. При ненулевых начю
усл-ях у имеющимся в цепи источникам
э.д.с. добавляются дополнительные
источники энергии. Величины э.д.с.
дополнительных источников определяются
запасами энергии в индуктивности и
ёмкости и равно в операторном виде
соответственно Li(0)
и –
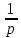
 (0).
(0).
48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
Рассмотрим
д.у. a∙
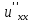 +b∙
+b∙
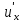 +cu
+∙
+cu
+∙
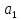 ∙
∙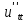 +
+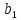 ∙
∙ =
0 – формула(1),a,
b,
c,
=
0 – формула(1),a,
b,
c,
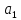 ,
,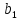 - непрерывные ф-ии, зависящие только от
х, заданные на отрезке [0,
- непрерывные ф-ии, зависящие только от
х, заданные на отрезке [0, ].
Считаем, чтоa
> 0 и будем рассматривать 2 случая: 1.
].
Считаем, чтоa
> 0 и будем рассматривать 2 случая: 1.
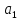 <
0 (гиперболический случай), 2.
<
0 (гиперболический случай), 2.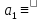 0,
0,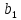 < 0 (параболический случай). Нужно найти
решениеu(x,t)
д.у. (1) для 0 ≤ x
≤
< 0 (параболический случай). Нужно найти
решениеu(x,t)
д.у. (1) для 0 ≤ x
≤
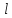 иt
≥ 0, удовл-щее нач. условиям u(x,0)
=
иt
≥ 0, удовл-щее нач. условиям u(x,0)
=
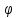 (x)
(для параболического случая), u(x,0)
=
(x)
(для параболического случая), u(x,0)
=
 (x),
(x),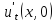 =
=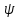 (x)
(для гиперболического), и краевым условиям
u(0,t)=
f(t),
α
(x)
(для гиперболического), и краевым условиям
u(0,t)=
f(t),
α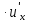 (
(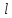 ,t)
+ β∙
,t)
+ β∙
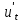 (
(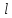 ,t)
=
,t)
=
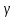 u(
u(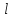 ,t),
где α, β,
,t),
где α, β,
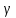 -
постоянные. При
-
постоянные. При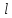 →
→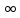 второе граничное условие отпадает.
Предполагая, что u,
второе граничное условие отпадает.
Предполагая, что u,
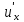 и
и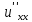 ,
рассматриваемые как функции переменнойt,
являются оригиналами, обозначим через
U(p,x)=
,
рассматриваемые как функции переменнойt,
являются оригиналами, обозначим через
U(p,x)=
 u(x,t)exp(-pt)dt
изображение функции u.
Тогда имеем
u(x,t)exp(-pt)dt
изображение функции u.
Тогда имеем
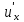
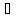
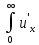 exp(-pt)dt
=
exp(-pt)dt
=
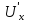 ,
,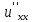

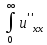 exp(-pt)dt
=
exp(-pt)dt
=
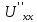 .
По правилу дифференцирования оригиналов:
.
По правилу дифференцирования оригиналов: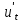
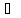 pU
– u(x,0),
pU
– u(x,0),


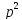 U
– u(x,0)p
-
U
– u(x,0)p
-
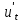 (x,0).
С учётом начальных условий:
(x,0).
С учётом начальных условий:
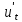
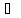 pU
–
pU
–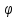 (x),
(x),
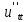
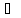
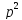 U
–
U
–
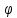 (x)p
-
(x)p
-
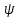 (x).
Предполагаем, что f(t)
является оригиналом и F(p)
(x).
Предполагаем, что f(t)
является оригиналом и F(p)
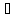 f(t),
тогда из граничных условий имеем
f(t),
тогда из граничных условий имеем
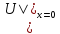 =F(p),
(α
=F(p),
(α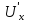 +
β(pU-
+
β(pU-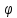 ))
))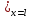 =
=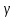
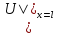 .
Операционный метод приводит решение
нестационарной задачи для ур-ия (1) с
частными производными к решению
обыкновенного д.у.a∙
.
Операционный метод приводит решение
нестационарной задачи для ур-ия (1) с
частными производными к решению
обыкновенного д.у.a∙
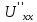 +b∙
+b∙
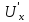 +AU
+ B,
где A
= с +
+AU
+ B,
где A
= с +
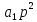 +
+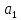 p,
B=
–
p,
B=
–
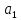 p
p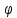 -
-
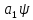 -
-
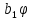 ,
p
– комплексный параметр, при граничных
условиях:
,
p
– комплексный параметр, при граничных
условиях:
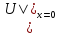 =F(p),
(
=F(p),
(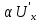 + (βp
–
+ (βp
–
 )U
- β
)U
- β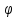 )
)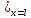 = 0.
= 0.
