
- •1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- •2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
- •2.Однородные ду
- •5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
- •8.Линейная зависимость,независимость ф-ий. Определитель вронского.
- •9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
- •12Линейные однородные системы ду высших порядков с постоянными коэффициентами
- •13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
- •15 Устойчивость по Ляпунову
- •16 Устойчивость по первому приближению
- •19.Предел и непрерывность функций комплексной переменной.
- •22.Элеменарные функции комплексной переменной.
- •25.Теорема Коши и интегральная формула Коши.
- •26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
- •27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
- •28. Нули аналитических функций. И их классификация.
- •29. Ряд Лорана. Изолированные особые точки и их классификация.
- •32. Вычет аналитических функций.
- •35.Классификац.Ур. Матфизики.
- •42. Оригинал и изображение. Св-ва преобразования Лапласа: линейность, подобие.
- •44. Формулы обращения преобразования Лапласа.
- •45. Применение преобразования Лапласа: теоремы обращения.
- •46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
- •47. Применение преобразования Лапласа к решению физических задач.
- •48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
19.Предел и непрерывность функций комплексной переменной.
Число
A≠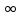 называется
пределом
функции f(z)
при
z→z0
и
обозначается А
=
называется
пределом
функции f(z)
при
z→z0
и
обозначается А
=
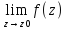 ,
если для любогоε>0
найдется δ=δ(ε)>0
такое, что для всех z≠z0,
удовлетворяющих неравенству │z
- z0│<
δ,
выполняется
неравенство │f(z)-А│<
ε.
,
если для любогоε>0
найдется δ=δ(ε)>0
такое, что для всех z≠z0,
удовлетворяющих неравенству │z
- z0│<
δ,
выполняется
неравенство │f(z)-А│<
ε.
Следует иметь ввиду, что для данной функции f(z) существование предела по любому фиксированному пути (z→z0) еще не гарантирует существования предела f(z) при z→z0.
Функция
f(z)
называется
непрерывной
в точке z0,
если
она определена в этой точке и
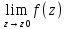 =
f(z0).
=
f(z0).
Функция f(z), непрерывная в каждой точке области D, называется непрерывной в этой области.
Функция f(z) называется равномерно непрерывной в области D, если для любого ε > О найдется δ=δ(ε)>0 такое, что для любых точек z1 и z2 из области D таких, что │z1 – z2│< δ, выполняется неравенство │f(z1) – f(z2)│< ε.
20-1.Производная аналитической функции. Условия Каши-Римана.
Пусть функция w=f(z) определена в некоторой области D комплексной переменной z.
Производной
функции f{z)
в точке z
называется
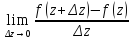 в
точкеz
и обозначается через f
’(z)
или
в
точкеz
и обозначается через f
’(z)
или
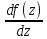 .
.
Если
в точке z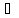 D
функция
f(z)
имеет производную f
’(z),
то говорят, что функция f(z)
дифференцируема в точке z.
D
функция
f(z)
имеет производную f
’(z),
то говорят, что функция f(z)
дифференцируема в точке z.
Функция
f(z),
дифференцируемая в каждой точке области
D
и
имеющая в этой области непрерывную
производную f
’(z),
называется аналитической
в области D.
Будем
также говорить, что f(z)
аналитическая в точке z0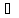 D,
если f(z)
является аналитической в некоторой
окрестности точки z0.
D,
если f(z)
является аналитической в некоторой
окрестности точки z0.
Теорема
.
Для того, чтобы функция f(z)
= u(x,y)
+ iv(x,y)
была аналитической в области D,
необходимо и достаточно существование
в этой области непрерывных частных
производных функций u(х,у)
и v(x,у),
удовлетворяющих условиям Коши-Римана:
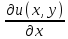 =
=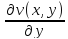 и
и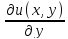 =
=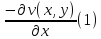 ;
;
Доказательство. Докажем необходимость условий Коши-Римана. По предположению, существует предел
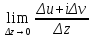 =
f
‘(z);
Поскольку
этот предел не зависит от характера
стремления
=
f
‘(z);
Поскольку
этот предел не зависит от характера
стремления
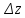 =
=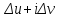 к нулю, то, устремляя Δz
к нулю по вертикальному и по горизонтальному
отрезкам, т.е. полагая первый раз Δу = 0,
Δх→0,
а второй раз Δx
= 0, Δу→0,
получаем: f
‘(z)=
к нулю, то, устремляя Δz
к нулю по вертикальному и по горизонтальному
отрезкам, т.е. полагая первый раз Δу = 0,
Δх→0,
а второй раз Δx
= 0, Δу→0,
получаем: f
‘(z)=
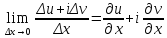 иf
‘(z)=
иf
‘(z)=
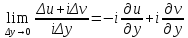 ;
;
20-2.
Сравнивая действительные и мнимые части в последних формулах, получаем условия (1).
Покажем
теперь, что выполнение условий (1) в
области D.
при
дополнительном требовании существования
полных дифференциалов у функций u(х,у)
и
v(x,y),
является достаточным для дифференцируемоести
функции f(z)
в
области D. В самом деле, существование
полных дифференциалов du
и
dv
равносильно
равенствам: Δu=
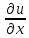 Δx
+
Δx
+
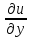 Δy
+ η1(x,y,Δx,Δy);
Δv=
Δy
+ η1(x,y,Δx,Δy);
Δv=
 Δx
+
Δx
+
 Δy
+ η2(x,y,Δx,Δy),
где величины η1
и η2
являются
бесконечно малыми высшего порядка по
отношению к │Δz│
= ((Δx)2
+ (Δy)2)1/2
при
Δz→0.
Вводя обозначения
Δy
+ η2(x,y,Δx,Δy),
где величины η1
и η2
являются
бесконечно малыми высшего порядка по
отношению к │Δz│
= ((Δx)2
+ (Δy)2)1/2
при
Δz→0.
Вводя обозначения
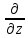 =
=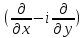 /2;
/2;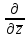 =
= /2;
будем иметь: Δf=
/2;
будем иметь: Δf=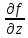 Δz
+
Δz
+
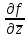 Δ
Δ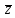 + η1
+ η2.
+ η1
+ η2.
Используя
комплексную запись
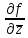 =
0 условий (1) и принимая во внимание
равенство
=
0 условий (1) и принимая во внимание
равенство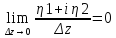 ,
получим, что существует предел
,
получим, что существует предел =
=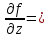 f'
‘(z),
т.е. функция в области D
дифференцируема.
□
f'
‘(z),
т.е. функция в области D
дифференцируема.
□
При
выполнении условий (1) производная f '(z)
может быть записана соответственно: f
'(z) =
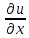 + i
+ i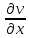 =
=
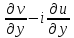 =
=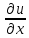 -i
-i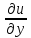 =
=
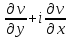 .
.
Формулы дифференцирования функций комплексной переменной аналогичны соответствующим формулам дифференцирования функций действительной переменной.
21.Связь аналитических и гармонических функций. Геометрический смысл модуля и аргумента производной.
1.Пусть
в области D
комплексн.плоскоти z
задана аналиттич.функц.
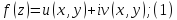 .Тогда
всюду в этой области функ.u
и v
связвны условием Коши-Римана:
.Тогда
всюду в этой области функ.u
и v
связвны условием Коши-Римана:
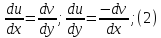 .Так
как аналитическая функция имеет в
области D производные всех порядков, то
и функцииu(х,
у) и v(x, у) имеют в соответствующей области
плоскости x, у частные производные любого
порядка. Это позволяет дифференцировать
(2) по переменным х, у любое число раз.
Продифференцировав (2) по х, второе - по
у и сложив, получим:
.Так
как аналитическая функция имеет в
области D производные всех порядков, то
и функцииu(х,
у) и v(x, у) имеют в соответствующей области
плоскости x, у частные производные любого
порядка. Это позволяет дифференцировать
(2) по переменным х, у любое число раз.
Продифференцировав (2) по х, второе - по
у и сложив, получим:
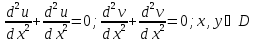
u(x,y) и v(x,y)гармонические в D плоскости
x,y и они связан. условием (1). Тем самым
необходимым и достаточным условием
аналитичности функции(1) в области D
является требование, чтобы u(х,
у) и v(x,
у) были гармоническими и удовлетворяли
условиям (2) в соответствующей области
плоскости x, у.
u(x,y) и v(x,y)гармонические в D плоскости
x,y и они связан. условием (1). Тем самым
необходимым и достаточным условием
аналитичности функции(1) в области D
является требование, чтобы u(х,
у) и v(x,
у) были гармоническими и удовлетворяли
условиям (2) в соответствующей области
плоскости x, у.
2.Пусть
функция
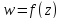 аналитичиа в точке
аналитичиа в точке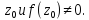
Геом.
смысл модуля производ.: величина
 определяет
коэффициент растяжения (подобия) в точке
определяет
коэффициент растяжения (подобия) в точке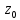 при отображении
при отображении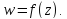 Величину
Величину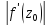 называют
коэффициентом растяжения, если
называют
коэффициентом растяжения, если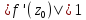 ,
или коэффициентом сжатия
,
или коэффициентом сжатия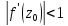 .
.
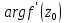 -это
угол, на который нужно повернуть
касательную к кривой l
в точке
-это
угол, на который нужно повернуть
касательную к кривой l
в точке
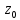 для того, чтобы получить направление
касательной к кривой L в точке
для того, чтобы получить направление
касательной к кривой L в точке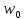 (точка
с полож.направлением действит.осей на
плоскостиz
и w).
Или
(точка
с полож.направлением действит.осей на
плоскостиz
и w).
Или
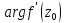 — это угол между отображенным и
первоначальным направлениями
касательных к кривым I и L в точках
— это угол между отображенным и
первоначальным направлениями
касательных к кривым I и L в точках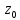 и
и соответственно.геом.
смысл аргумента производ.
соответственно.геом.
смысл аргумента производ.
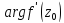 .
.
