
- •1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- •2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
- •2.Однородные ду
- •5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
- •8.Линейная зависимость,независимость ф-ий. Определитель вронского.
- •9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
- •12Линейные однородные системы ду высших порядков с постоянными коэффициентами
- •13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
- •15 Устойчивость по Ляпунову
- •16 Устойчивость по первому приближению
- •19.Предел и непрерывность функций комплексной переменной.
- •22.Элеменарные функции комплексной переменной.
- •25.Теорема Коши и интегральная формула Коши.
- •26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
- •27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
- •28. Нули аналитических функций. И их классификация.
- •29. Ряд Лорана. Изолированные особые точки и их классификация.
- •32. Вычет аналитических функций.
- •35.Классификац.Ур. Матфизики.
- •42. Оригинал и изображение. Св-ва преобразования Лапласа: линейность, подобие.
- •44. Формулы обращения преобразования Лапласа.
- •45. Применение преобразования Лапласа: теоремы обращения.
- •46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
- •47. Применение преобразования Лапласа к решению физических задач.
- •48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
16 Устойчивость по первому приближению
Пусть имеем динамическую систему
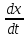 1=f1(t,x1,…,xn),………………………,
(1)
1=f1(t,x1,…,xn),………………………,
(1)
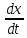 n=fn(t,x1,…,xn)
n=fn(t,x1,…,xn)
с точкой покоя О(0;0), где ф-ии f(x,y) и g(x,y) непрерывно дифференцируемы в некоторой окрестности начала координат.
Разложим ф-ии f(x,y) и g(x,y) по ф-ле Тейлора по x,y в окрестности начала координат:
f(x,y)=ах+by+R1(x,y),
g(x,y)=cx+dy+R2(x,y),
где а= ,b=
,b=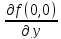 ,c=
,c=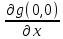 ,d=
,d=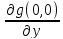 ,
аR1,R2
– члены второго порядка малости
относительно x,y.
,
аR1,R2
– члены второго порядка малости
относительно x,y.
Тогда
исходная система (1) примет вид:
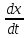 =ax+by+R1(x,y),
(2)
=ax+by+R1(x,y),
(2)
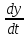 =cx+dy+R2(x,y),
=cx+dy+R2(x,y),
Вместо
(2) рассмотрим систему:
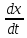 =ax+by
(3)
=ax+by
(3)
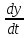 =cx+dy
=cx+dy
(3)- система уравнений первого приближения для системы(1)
Замечание1.
Если точка (х0;у0)-
некоторое другое положение равновесия
системы(1), то система первого приближения
строится так: в системе(1) сначала сделаем
замену x=u+x0,
y=ν+y0
и получим ф-ии
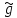 (u,ν)=g(u+x0,ν+y0),
(u,ν)=g(u+x0,ν+y0),
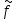 (u,ν)=f(u+x0,ν+y0),
а дальше поступаем так же, как и раньше
с заменой х на u,
а у на ν.
(u,ν)=f(u+x0,ν+y0),
а дальше поступаем так же, как и раньше
с заменой х на u,
а у на ν.
Справедливы следующие выражения:
1.Если все корни характеристического ур-я
λ2-Sp Aλ+detA=0 (4)
имеют отрицательные вещественные части, то нулевое решение х=у=0 системы (3) и системы (2) асимптотически устойчиво
2.Если хотя бы 1-н корень ур-я (4) имеет положительную вещественную часть, то нулевое решение системы (3) и системы (2) неустойчиво.
Говорят, что в случаях 1 и 2 возможно исследование на устойчивость по 1-му приближению.
17-1.Фазовая плоскость и особые точки двумерных систем.
Рассмотрим
систему двух линейных уравнений с
постоянными коэффициентами:
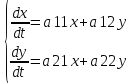
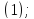
Очевидно,
что x(t)=0
и
y(t)=0
является
решением системы, удовлетворяющим
нулевым начальным условиям х(0)=0,
у(0)=0.
Предполагаем, что начало координат O
(0;
0) является единственной точкой покоя
системы (1), т.е. Δ= =0.
Будем искать общее решение системы (1)
методом Эйлера. Характеристическое
уравнение имеет вид:
=0.
Будем искать общее решение системы (1)
методом Эйлера. Характеристическое
уравнение имеет вид: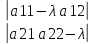 =λ2-(α11+α22)λ+(α11α22-α12α21)=0
(2);
Из
(2) следует, что λ=0 не может быть корнем
характеристического уравнения.
Возможны случаи:
=λ2-(α11+α22)λ+(α11α22-α12α21)=0
(2);
Из
(2) следует, что λ=0 не может быть корнем
характеристического уравнения.
Возможны случаи:
1.
Корни
λ1
и
λ2
действительные и различные. Пусть γ1=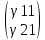 иγ2=
иγ2=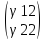 - собственные векторы матрицы А=
- собственные векторы матрицы А= ,
соответствующие характеристическим
числам λ1
и
λ2.
Тогда
общее решение системы (1) имеет вид:
х=С1γ11eλ1t
+ C2
γ12eλ2t,
y=
С1γ21eλ1t
+ C2
γ22eλ2t
(3), где С1
и
С2
– произвольные постоянные.
,
соответствующие характеристическим
числам λ1
и
λ2.
Тогда
общее решение системы (1) имеет вид:
х=С1γ11eλ1t
+ C2
γ12eλ2t,
y=
С1γ21eλ1t
+ C2
γ22eλ2t
(3), где С1
и
С2
– произвольные постоянные.
1.1. Если λ1<0, λ2<0 то из (3) видно, что точка покоя асимптотически устойчива и называется устойчивым узлом (рис.1).

Рис. 1 Рис. 2 Рис. 3
1.2. Если λ1>0, λ2 >0, узел неустойчивый (рис.2).
1.3. Если λ1 λ2<0, то точка покоя называется седлом (рис.3).
17-2.
2. Корни λ1 и λ2 комплексные, т.е. λ1=α + iβ, λ1=α - iβ. Общим решением системы (1) будет
х = еαt (С11 cosβt + С12 sinβt), у = еαt (С21 cosβt + С22 sinβt) (4), где С11,С12,С21,С22 - являются линейными комбинациями произвольных постоянных С1,С2.
2.1.
Если α<0,
то, на основании (4), заключаем, что при
t→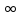 точка (х;у)→О(0;0).
Положение равновесия в этом случае
называют устойчивым
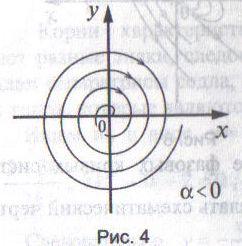
фокусом (рис.4).
точка (х;у)→О(0;0).
Положение равновесия в этом случае
называют устойчивым
фокусом (рис.4).
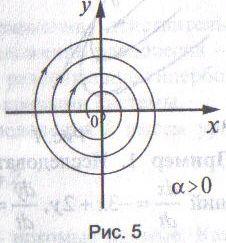
2.2.
Если а
> 0,
то точка покоя - неустойчивый
фокус, т.е.
при t→ точка (х;у)
бесконечно
удаляется от начала координат (рис.5).
точка (х;у)
бесконечно
удаляется от начала координат (рис.5).
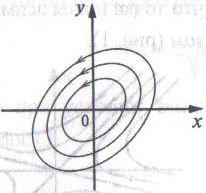
2.3. Если а=0, общее решение системы принимает вид х= С11 cosβt + С12 sinβt, y= С21 cosβt + С22 sinβt (5).
Фазовые траектории являются эллипсами с центром в точке (0;0). Положение равновесия называется центром (рис. 6).
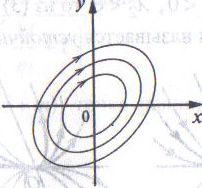
3. Корни кратные, т.е. λ1=λ2= λ. Общее решение имеет вид: х=(С1+С2t)eλt , y= (С3+С4t)eλt (6),
где C1, C2, C3, C4 - линейные комбинации произвольных постоянных С1,С2 .
При
λ<0 и t→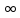 точка
(х;у)→(0;0).
Положение равновесия будет асимптотически
устойчивым и называется вырожденным
узлом (рис.7).
точка
(х;у)→(0;0).
Положение равновесия будет асимптотически
устойчивым и называется вырожденным
узлом (рис.7).
При
λ>0 и t→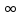 точка
бесконечно удаляется от начала координат
(х;у).
Вырожденный
узел будет неустойчивым (рис.8).
точка
бесконечно удаляется от начала координат
(х;у).
Вырожденный
узел будет неустойчивым (рис.8).


18.Комплексные
числа, арифметические операции. Формулы
Эйлера.
Комплексным
числом
z
называется
упорядоченная пара действительных
чисел (a;b),
которая
записывается в виде z
= (a;b).
Число а называется действительной
частью комплексного числа z (a=Rez),
а число b
–
мнимой частью z (b=Imz). Любое действительное
число а можно рассматривать как пару
(а,0)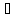 С.
Особую роль играет пара (0,1), т.к. (0,1)2=-1.
Пару (0,1) обозначают буквой i, где i –
мнимая единица, т.е. i2=-1.
С учётом последнего обозначения
комплексное число можно записать в
виде: z=a+ib. Такую форму записи называют
алгебраической.
Арифметические операции: 1.z1
+ z2
=(a1,b1)
+ (a2,b2)
=(a1
+ a2,
b1
+ b2).
2.
z1z2=
(a1,b1)
(a2,b2)
= (a1a2
– b1b2,a1b2
+a2b1).
С.
Особую роль играет пара (0,1), т.к. (0,1)2=-1.
Пару (0,1) обозначают буквой i, где i –
мнимая единица, т.е. i2=-1.
С учётом последнего обозначения
комплексное число можно записать в
виде: z=a+ib. Такую форму записи называют
алгебраической.
Арифметические операции: 1.z1
+ z2
=(a1,b1)
+ (a2,b2)
=(a1
+ a2,
b1
+ b2).
2.
z1z2=
(a1,b1)
(a2,b2)
= (a1a2
– b1b2,a1b2
+a2b1).
Число
z1=a-ib
называют сопряженным к комплексному
числу z и обозначают
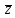 =a-ib.
=a-ib.
Комплексные числа обладают всеми свойствами действительных чисел, за исключением отношения порядка. Имеет место формула Эйлера: еiφ=cosφ +isinφ, e0=1, e2πki=-1, значит функция ея периодическая. T0=2πi – её минимальный период. С учётом формулы Эйлера получают: cosφ= (eiφ + e-iφ)/2; sinφ= (eiφ - e-iφ)/2i.
