
- •1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- •2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
- •2.Однородные ду
- •5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
- •8.Линейная зависимость,независимость ф-ий. Определитель вронского.
- •9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
- •12Линейные однородные системы ду высших порядков с постоянными коэффициентами
- •13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
- •15 Устойчивость по Ляпунову
- •16 Устойчивость по первому приближению
- •19.Предел и непрерывность функций комплексной переменной.
- •22.Элеменарные функции комплексной переменной.
- •25.Теорема Коши и интегральная формула Коши.
- •26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
- •27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
- •28. Нули аналитических функций. И их классификация.
- •29. Ряд Лорана. Изолированные особые точки и их классификация.
- •32. Вычет аналитических функций.
- •35.Классификац.Ур. Матфизики.
- •42. Оригинал и изображение. Св-ва преобразования Лапласа: линейность, подобие.
- •44. Формулы обращения преобразования Лапласа.
- •45. Применение преобразования Лапласа: теоремы обращения.
- •46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
- •47. Применение преобразования Лапласа к решению физических задач.
- •48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
44. Формулы обращения преобразования Лапласа.
1.
Изображением ф-ции
f(t)
(по Лапласу) наз. ф-ия f(t)
комплексного переменного p=s+iδ,
определяемая равенством: F(p)
=
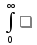 f(t)
f(t) dt
, которое ставит в соответствие оригиналу
f(t)
его изображение F(p)
и называется преобразованием Лапласа.
2.
Линейность.
Для любых комплексных постоянных α и β
имеет место αf(t)
+ βg(t)
dt
, которое ставит в соответствие оригиналу
f(t)
его изображение F(p)
и называется преобразованием Лапласа.
2.
Линейность.
Для любых комплексных постоянных α и β
имеет место αf(t)
+ βg(t)
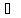 αF(p)
+ βG(p),
т.е. линейной комбинации оригиналов
соответствует линейная такая же
комбинация изображений. 2.
Подобие.
Для любого α>0 имеет место f(αt)
αF(p)
+ βG(p),
т.е. линейной комбинации оригиналов
соответствует линейная такая же
комбинация изображений. 2.
Подобие.
Для любого α>0 имеет место f(αt)
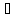
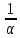 F(
F(
 ), т.е. умножение аргумента на положительное
числоα
приводит к делению изображения аргумента
на это число.
3. Дифференцирование оригинала.
Если f
’(t),
f
‘’(t),…,
), т.е. умножение аргумента на положительное
числоα
приводит к делению изображения аргумента
на это число.
3. Дифференцирование оригинала.
Если f
’(t),
f
‘’(t),…,
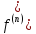 t)
– оригиналы и f
(t),
f
‘(t),…,
t)
– оригиналы и f
(t),
f
‘(t),…,
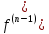 t)
– непрерывны, то: f
’(t)
t)
– непрерывны, то: f
’(t)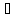 p∙F(p)-f(0);
f
‘’(t)
p∙F(p)-f(0);
f
‘’(t)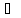
 F(p)-pf(0)-f
’(0);
F(p)-pf(0)-f
’(0);
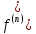 t)
t)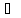
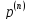 F(p)
-
F(p)
-
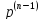 f(0)
-…-
f(0)
-…-
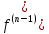 0).
4.Дифференцирование
изображения.
Дифференцированию изображения
соответствует умножение его оригинала
на (–t),
т.е. F
’(p)
0).
4.Дифференцирование
изображения.
Дифференцированию изображения
соответствует умножение его оригинала
на (–t),
т.е. F
’(p)
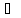 –t∙f(t);
–t∙f(t);
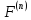 (p)
=
(p)
=
 ∙
∙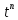 ∙f(t).
5.
Интегрирование оригинала.
∙f(t).
5.
Интегрирование оригинала.
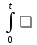 f(τ)dτ
f(τ)dτ
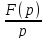 ,
т.е. интегрированию оригинала от 0 доt
соответствует деление его изображения
на p.
6.
Интегрирование изображения.
Если
,
т.е. интегрированию оригинала от 0 доt
соответствует деление его изображения
на p.
6.
Интегрирование изображения.
Если
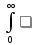 F(z)dz
сходится, то
F(z)dz
сходится, то
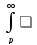 F(z)dz
F(z)dz
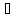
 , т.е. интегрированию изображения отp
до
, т.е. интегрированию изображения отp
до
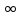 соответствует деление его оригинала
наt.
7.
Запаздывание.
Для любого τ
>0 имеем f(t-τ)
соответствует деление его оригинала
наt.
7.
Запаздывание.
Для любого τ
>0 имеем f(t-τ)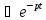 F(p),
т.е. запаздывание оригинала на положительную
величину τ
приводит к умножению изображения без
запаздывания на
F(p),
т.е. запаздывание оригинала на положительную
величину τ
приводит к умножению изображения без
запаздывания на
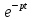 .
8.
Умножение изображений.
F(p)∙G(p)
.
8.
Умножение изображений.
F(p)∙G(p)

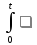 f(τ)
g(t-
τ)dτ.
9.
Умножение оригиналов.
f(t)
∙ g(t)
f(τ)
g(t-
τ)dτ.
9.
Умножение оригиналов.
f(t)
∙ g(t)
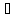
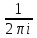
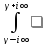 F(z)
G(p-z)dz
, гдк путь интегрирования – вертикальная
прямая Re
z
=
F(z)
G(p-z)dz
, гдк путь интегрирования – вертикальная
прямая Re
z
=
 .10.
Т1.
Если ф-я F(p)
в окрестности точки p=
.10.
Т1.
Если ф-я F(p)
в окрестности точки p=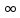 может быть представлена в виде ряда
Лорана: F(p)=
может быть представлена в виде ряда
Лорана: F(p)=
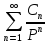 =
= +
+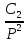 +…, то ф-яf(t)=
+…, то ф-яf(t)=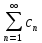 ∙
∙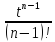 =
=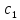 +
+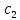 t
+…(t
> 0) является оригиналом, имеющим
изображение F(p),
т.е. F(p)=
t
+…(t
> 0) является оригиналом, имеющим
изображение F(p),
т.е. F(p)=
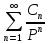
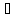
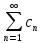 ∙
∙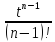 =f(t).
11.
Т2.
Если F(p)=А(р)/B(р)
– правильная рациональная дробь,
знаменатель которой В(р) имеет простые
корни
=f(t).
11.
Т2.
Если F(p)=А(р)/B(р)
– правильная рациональная дробь,
знаменатель которой В(р) имеет простые
корни
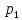 ,
,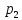 ,
… ,
,
… ,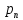 , то ф-ияf(t)
=
, то ф-ияf(t)
=
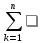 [(A(
[(A(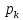 )/B’(
)/B’(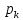 ))
∙exp(
))
∙exp( )]
явл. Оригиналом, имеющим изображениеF(p),
а F(p)
= (А(р)/B(р))
)]
явл. Оригиналом, имеющим изображениеF(p),
а F(p)
= (А(р)/B(р))
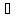
 Res[F(
Res[F(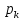 )exp(
)exp( )]
=f(t).
)]
=f(t).
45. Применение преобразования Лапласа: теоремы обращения.
Т1.
Если ф-я F(p)
в окрестности точки p=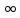 может быть представлена в виде ряда
Лорана:
может быть представлена в виде ряда
Лорана:
F(p)=
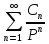 =
=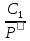 +
+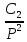 +…, то ф-яf(t)=
+…, то ф-яf(t)=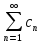 ∙
∙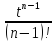 =
=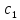 +
+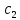 t
+…(t
> 0) является оригиналом, имеющим
изображение F(p),
т.е. F(p)=
t
+…(t
> 0) является оригиналом, имеющим
изображение F(p),
т.е. F(p)=
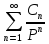
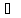
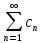 ∙
∙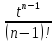 =f(t).
Док-во:
Ряд
=f(t).
Док-во:
Ряд
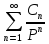 сходится в некоторой окрестности
бесконечно удалённой точки, т.е. существуетR,
что этот ряд сходится при |p|
> R.
Тогда ряд
сходится в некоторой окрестности
бесконечно удалённой точки, т.е. существуетR,
что этот ряд сходится при |p|
> R.
Тогда ряд
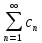 ∙
∙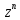 = Ψ(z)
сходится при |z|
< 1/R.
Пусть
= Ψ(z)
сходится при |z|
< 1/R.
Пусть
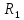 < 1/R.
Ряд для Ψ(z)
сходится в замкнутом круге |z|
<
< 1/R.
Ряд для Ψ(z)
сходится в замкнутом круге |z|
<
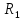 , сумма его непрерывна в этом круге и
поэтому ограничена: |Ψ(z)|
< M.
Используя оценки Коши коэффициентов
ряда Тейлора |
, сумма его непрерывна в этом круге и
поэтому ограничена: |Ψ(z)|
< M.
Используя оценки Коши коэффициентов
ряда Тейлора |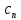 |
<M/
|
<M/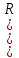 )
и предполагая, что 0 <t
<
)
и предполагая, что 0 <t
<
 ,
получаем
,
получаем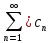 ∙
∙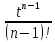 |
< (M/
|
< (M/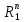 )
∙
)
∙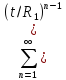 /
/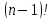 )
= (M/
)
= (M/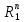 )
∙exp(
)
∙exp(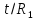 ).
Следовательно, ряд дляf(t)
сходится при 0 < t
<
).
Следовательно, ряд дляf(t)
сходится при 0 < t
<
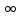 и ф-ияf(t)
является оригиналом. Применяя
и ф-ияf(t)
является оригиналом. Применяя

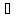 n!/
n!/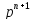 ,
получимf(t)
=
,
получимf(t)
=
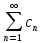 ∙
∙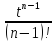 .
.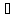 Т2.
Если F(p)=А(р)/B(р)
– правильная рациональная дробь,
знаменатель которой В(р) имеет простые
корни
Т2.
Если F(p)=А(р)/B(р)
– правильная рациональная дробь,
знаменатель которой В(р) имеет простые
корни
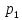 ,
,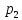 ,
… ,
,
… ,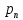 , то ф-ияf(t)
=
, то ф-ияf(t)
=
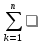 [(A(
[(A(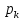 )/B’(
)/B’(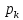 ))
∙exp(
))
∙exp(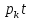 )]
явл. Оригиналом, имеющим изображениеF(p),
а F(p)
= (А(р)/B(р))
)]
явл. Оригиналом, имеющим изображениеF(p),
а F(p)
= (А(р)/B(р))
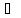
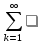 Res[F(
Res[F(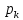 )exp(
)exp(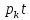 )]
=f(t).
)]
=f(t).
