
- •1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
- •2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
- •2.Однородные ду
- •5.Ду высшихпорядков: постановка задачи Коши, теорема сущ-ния и един-ти решения задачи Коши.
- •8.Линейная зависимость,независимость ф-ий. Определитель вронского.
- •9.Линейные однородные уравнения высших порядков с постоянными коэф-тами. Характеристическое ур-е Зависимость общего решения от корней характер-го ук-я.
- •12Линейные однородные системы ду высших порядков с постоянными коэффициентами
- •13.Линейные неоднородные системы ду высших порядков с постоянными коэффициентами. Системы со специальной правой частью.
- •15 Устойчивость по Ляпунову
- •16 Устойчивость по первому приближению
- •19.Предел и непрерывность функций комплексной переменной.
- •22.Элеменарные функции комплексной переменной.
- •25.Теорема Коши и интегральная формула Коши.
- •26. Cтепенные ряды в комплексной области. Теорема Абеля, радиус сходимости
- •27. Ряд Тейлора. Разложение некоторых элементарных функций в ряд Тейлора
- •28. Нули аналитических функций. И их классификация.
- •29. Ряд Лорана. Изолированные особые точки и их классификация.
- •32. Вычет аналитических функций.
- •35.Классификац.Ур. Матфизики.
- •42. Оригинал и изображение. Св-ва преобразования Лапласа: линейность, подобие.
- •44. Формулы обращения преобразования Лапласа.
- •45. Применение преобразования Лапласа: теоремы обращения.
- •46. Применение преобразования Лапласа. Решение линейных д. У. С помощью преобразований Лапласа.
- •47. Применение преобразования Лапласа к решению физических задач.
- •48. Решение ур-ий с частными производными с помощью преобразования Лапласа.
1.Дифференциальные уравнения(д.У.) первого порядка. Общее и частное решение д.У. Задача Коши.
Уравнения, связывающие независимую переменную, неизвестную функцию и её производные называют дифференциальным. Если искомая функция зависит от одной переменной, то Д.У. называют обыкновенным.
Если искомая функция зависит от нескольких переменных, то Д.У. называют уравнение частных производных.
Наивысший
порядок производной, входящий в Д.У.
называют порядком этого уравнения. Д.У.
первого порядка называют выражение
вида F(x,y,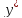 )=0(1).
Если это уравнение удаётся разрешить
относительно производной, то записывают
)=0(1).
Если это уравнение удаётся разрешить
относительно производной, то записывают
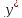 =
f(x,y)(2).
Решением уравнения (1)
и (2)
называют такую дифференцируемую функцию
y=
=
f(x,y)(2).
Решением уравнения (1)
и (2)
называют такую дифференцируемую функцию
y=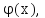 которая при подстановке её в уравнение
обращает его в верное тождество.
которая при подстановке её в уравнение
обращает его в верное тождество.
Задачей
Коши либо начальной задачей называют
задачу нахождения решения y=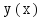 уравнения(2),
удовлетворяющего
начальному условию y(xo)=yo
(3).
уравнения(2),
удовлетворяющего
начальному условию y(xo)=yo
(3).
Общим
решением Д.У. (2)
называется
функция y=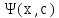 (4),
зависящая от переменной x и произвольной
постоянной c. Общее решение (4)
удовлетворяет
условию уравнения (2)
при
любых значениях константы с.
(4),
зависящая от переменной x и произвольной
постоянной c. Общее решение (4)
удовлетворяет
условию уравнения (2)
при
любых значениях константы с.
Каково
бы ни было начальное условие (3)
можно
подобрать значение со константы с, так
чтобы функция y=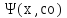 удовлетворяла заданному начальному
условию(3)(если
выполнены условия теоремы Коши).
удовлетворяла заданному начальному
условию(3)(если
выполнены условия теоремы Коши).
Частным решением Д.У. называют решение, полученное из общего решения (4) либо вида (4) при каком либо определённом значении постоянной произвольной с.
2. Теорема существования и единственности решения задачи Коши для дифференциального уравнения (д.У.) первого порядка.
Теорема
Коши (существования и единственности):
если функция f(x,y) непрерывна и имеет
непрерывную производную
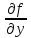 в областиD,
то решение Д.У.
в областиD,
то решение Д.У.
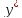 =
f(x,y) с начальным условием y(xo)=yo
, где точка с координатами (xo,yo) принадлежит
D, существует и единственно, то есть
через точку (xo,yo) принадлежащую области
D проходит единственная интегральная
кривая данного уравнения.
=
f(x,y) с начальным условием y(xo)=yo
, где точка с координатами (xo,yo) принадлежит
D, существует и единственно, то есть
через точку (xo,yo) принадлежащую области
D проходит единственная интегральная
кривая данного уравнения.
Если
во всех точках решения y = Ψ(x)
уравнения
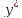 =
f(x,y) условие действительности не
выполняется, то такое решение называется
особым. При этом через каждую точку
Мо(xo,yo) особого решения проходит также
и другое решение уравнения
=
f(x,y) условие действительности не
выполняется, то такое решение называется
особым. При этом через каждую точку
Мо(xo,yo) особого решения проходит также
и другое решение уравнения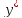 =
f(x,y), которое не совпадает с решением y
=Ψ(x)
в сколь угодно малой окрестности этой
точки.
=
f(x,y), которое не совпадает с решением y
=Ψ(x)
в сколь угодно малой окрестности этой
точки.
3.ДУ 1-го порядка,интегрируемые в квадратурах.
1.Ур-ия с разделяющимися переменними
P(xy)dx+Q(xy)dy=0 (1). Ур-е(1) наз. ур-ем,записанным в диф-лах.,где x-аргумент,y-искомая ф-я, dx,dy-диф-лы, P(xy), Q(xy)-заданные непрерывные в некот.области D ф-ии.
Пусть
P(xy)=p(x),а
Q(xy)=q(y),тогда
(1) примет вид (2): p(x)dx+q(y)dy=0.
(2)наз.ДУ с разделёнными переменнымы,
интегрируя которое мы получим: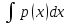 +
+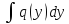 =C-общий
ин-л у-я(2). Если хотя бы один из интегралов
неберущ.,то ДУ(2) всё равно считается
решённым, при этом говорят, что решение
найдено в квадратурах.Пусть P(xy)=
=C-общий
ин-л у-я(2). Если хотя бы один из интегралов
неберущ.,то ДУ(2) всё равно считается
решённым, при этом говорят, что решение
найдено в квадратурах.Пусть P(xy)=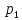 (x)*
(x)*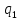 (y),
Q(xy)=
(y),
Q(xy)=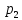 (x)*
(x)*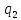 (y),
тогда (1) примет вид(3):
(y),
тогда (1) примет вид(3):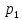 (x)*
(x)*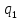 (y)dx+
(y)dx+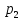 (x)*
(x)*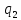 (y)dy=0.У-е
(3)-ДУ с разделяющимися переменными.Разделив
(3) на
(y)dy=0.У-е
(3)-ДУ с разделяющимися переменными.Разделив
(3) на
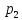 (x)*
(x)*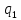 (y)
получаем:
(y)
получаем: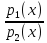 dx+
dx+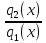 dy=0,которое
является ур-ем с разделёнными переменными:
dy=0,которое
является ур-ем с разделёнными переменными:
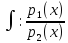 dx+
dx+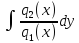 =C.
При таком решении могут быть потеряны
корни
=C.
При таком решении могут быть потеряны
корни
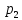 (x)=0
и
(x)=0
и
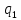 (y)=0,которые
необходимо рассматривать отдельно.
(y)=0,которые
необходимо рассматривать отдельно.
