13.. Стационарные и эргодические случайные процессы.

1. Стационарность. Случайные процессы, статистические характеристики которых одинаковы во всех сечениях называются стационарными случайными процессами. Различаются стационарные случайные процессы в узком смысле и широком смысле. Случайный процесс стационарен в узком смысле, если любая n-мерная плотность вероятности инвариантна относительно временного сдвига :

(6.1)

Если же ограничить требования тем, чтобы математическое ожидание m и дисперсия процесса не зависели от времени, а функция корреляции зависела лишь от разности, т.е., то подобный случайный процесс будет стационарен в широком смысле. Из стационарности в узком смысле следует стационарность в широком смысле, но не наоборот. Как следует из определения, функция корреляции стационарного случайного процесса является чётной:

Кроме того, абсолютные значения этой функции при любом не превышают её значения при:

(6.2)

Часто удобно использовать нормированную функцию корреляции:

(6.3)

Для которой

2. Эргодичность. Стационарный случайный процесс называется эргодическим, если при нахождении его моментных функций усреднение по статистическому ансамблю можно заменить усреднением по времени.

Операция усреднения выполняется над единственной реализацией x(t), длительность которой теоретически может быть сколь угодно велика. Обозначая усреднение по времени угловыми скобками, запишем математическое ожидание эргодического случайного процесса:

, (6.4)

которое равно постоянной составляющей выбранной реализации.

Дисперсия подобного процесса.

(6.5)

Поскольку величина представляет собой мощность реализации, а величина- мощность постоянной составляющей, дисперсия имеет наглядный смысл мощности флуктуационной составляющей эргодического процесса.

Аналогично находим функцию корреляции:

(6.6)

Достаточным условием эргодичности случайного процесса, стационарного в широком смысле, является стремление к нулю функции корреляции при неограниченном росте временного сдвига :

(6.7)

Это требование можно несколько ослабить и применительно к гармоническому процессу со случайной начальной фазой. Случайный процесс эргодичен если выполняется условие Слуцкого:

14 ..Спектральные представления случайных процессов. Теорема Винера-Хинчина.

Рассмотрим стационарный случайный процесс Х(t) c нулевым математическим ожиданием: . Отдельно взятая реализация этого процесса есть детерминированная функция, которую можно представить в виде обратного преобразования Фурье:

(6.9)

Свойства случайной спектральной плотности:

1) Прежде всего, усредним мгновенные значения сигналов x(t) по ансамблю реализаций и приравняем его к нулю.

Это равенство будет выполняться тождественно при любом значении t, если потребовать выполнения условия . Итак, случайная спектральная плотность отдельных реализаций стационарного случайного процесса должна иметь нулевое математическое ожидание на всех частотах.

2):

(6.10)

Запишем выражение функции корреляции процесса X(t), используя спектральные разложения случайных реализаций:

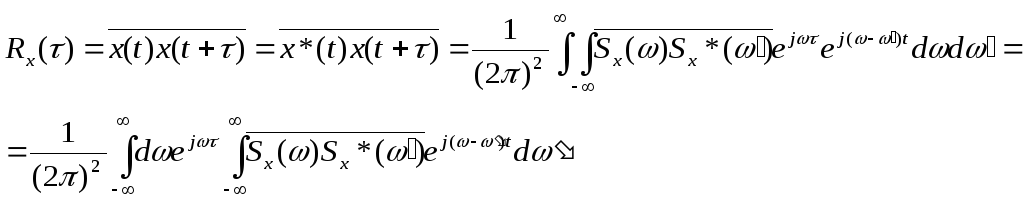
(6.11)

Здесь во внутреннем подынтегральном выражении содержится множитель , имеющий смысл функции корреляции случайной спектральной плотности. Для того чтобы функцияне зависела от времениt, необходимо, как это видно из выражения (6.11) выполнение следующей пропорциональности:

~(6.12)

Случайная спектральная плотность стационарного процесса имеет специфическую структуру; ее значения, отвечающие любым двум несовпадающим частотам, не коррелированы между собой. В то же время средний квадрат (дисперсия) случайной спектральной плотности неограниченно велик при любых частотах. Такой вид корреляционной связи называют дельта-коррелированностью.

Введём в формулу (6.12) множитель пропорциональности, зависящий от частоты, и запишем это равенство таким образом:

(6.13)

Функция называется спектральной плотностью мощности процесса Х(t) (спектром мощности). Если случайный сигнал является напряжением, то его спектр мощности имеет размерность , то есть размерность удельной мощности, выделяемой на единичном резисторе.

Подставив (6.13) в (6.11) приходим к важному результату:

(6.14)

(6.15)

Итак, функция корреляции и спектр мощности стационарного случайного процесса связаны между собой преобразованиями Фурье.

Формулы (6.14) и (6.15) составляют содержание теоремы Винера-Хинчина (1934 г. Хинчин А.Я. и Н. Винер).

Для того чтобы выяснить физический смысл дисперсии, положим в (6.14) Тогда поскольку, получаем

(6.16)

Следует подчеркнуть различие между энергетическим спектром детерминированного импульсного сигналаu(t) и спектральной плотностью мощности стационарного случайного процессаX(t). Функция характеризует меру энергии, приходящуюся на единичную полосу частот. В отличие от этого функцияхарактеризует удельную меру мощности. Этот факт находит отражение и в разных физических размерностях данных функций.

Свойства спектральной плотности мощности

1) По своему физическому смыслу спектр мощности вещественен и неотрицателен:

Поэтому по спектру мощности принципиально невозможно восстановить какую - либо отдельно взятую реализацию случайного процесса.

2) Поскольку чётная функция аргумента, то соответствующий спектр мощностипредставляет собой чётную функцию частоты. Отсюда следует, что пару преобразований Фурье (6.14), (6.15) можно записать, используя интегралы в полубесконечных пределах:

(6.17)

(6.18)

3. Целесообразно ввести так называемый односторонний спектр мощности случайного процесса, определив его следующим образом:

(6.19)

Функция позволяет вычислить дисперсию стационарного случайного процесса путём интегрирования по положительным (физическим частотам):

(6.20)

4. В технических расчётах часто вводят односторонний спектр мощности N(f), представляющий собой среднюю мощность случайного процесса, приходящуюся на интервал частот шириной в 1 Гц:

(6.21)

При этом, как легко видеть

Весьма важным параметром случайных процессов является интервал корреляции. Случайные процессы, как правило, обладают следующими свойствами: их функция корреляции стремится к нулю с увеличением временного сдвига . Чем быстрее убывает функция, тем меньше оказывается статистическая связь между мгновенными значениями случайного сигнала в два несовпадающих момента времени.

Числовой характеристикой, служащей для оценки «скорости изменения» реализации случайного процесса, является интервал корреляции определяемый выражением:

(6.22)

Если известна информация о поведении какой-либо реализации «в прошлом», то возможен вероятностный прогноз случайного процесса на время порядка .

Ещё одним существенным параметром для случайного процесса является эффективная ширина спектра. Пусть исследуемый случайный процесс характеризуется функцией - односторонним спектром мощности, причём- экстремальное значение этой функции. Заменим мысленно данный случайный процесс другим процессом, у которого спектральная плотность мощности постоянна и равнав пределах эффективной полосы частот, выбираемой из условия равенства средних мощностей обоих процессов:

Отсюда получается формула для эффективной ширины спектра:

(6.23)

Вне пределов указанной полосы спектральная плотность случайного процесса считается равной 0.

Этой числовой характеристикой часто пользуются для инженерного расчёта дисперсии шумового сигнала: .

Если реализации случайного процесса имеют размерность напряжения (В), то относительный спектр мощности N имеет размерность .