26 ..Информация в непрерывных сигналах. Дифференциальная энтропия.

Обобщим теперь понятия энтропии и взаимной информации на ансамбли непрерывных сигналов. Пусть - случайная величина (сечение или отсчёт случайного сигнала), определённая в некоторой непрерывной области, и её распределение вероятностей характеризуется плотностью.

Разобьём область значений на небольшие интервалы протяжённостью. Вероятность того, чтолежит в интервале,+, то есть, приблизительно равна, причём приближение тем точнее, чем меньше интервал. Степень неожиданности такого события равна. Если значенияв пределах конечного интервалазаменить значениямив начале интервала, то непрерывный ансамбль заменится дискретным, а его энтропия определится как:

Будем теперь увеличивать точность определения значения , уменьшая интервал. В пределе, придолжна получиться энтропия непрерывной случайной величины:

(10.18)

Попытаемся теперь определить взаимную информацию между двумя непрерывными случайными величинами и. Разбив области определенияисоответственно на небольшие интервалыи, заменим эти непрерывные величины дискретными так же, как это делалось при выводе формулы. Исходя из этого выражения можно определить взаимную информацию между непрерывными величинамии:

(10.19)

При этом никаких явных бесконечностей не появилось, и действительно, в обычных случаях взаимная информация оказывается конечной. С помощью простых преобразований её можно представить и в таком виде: 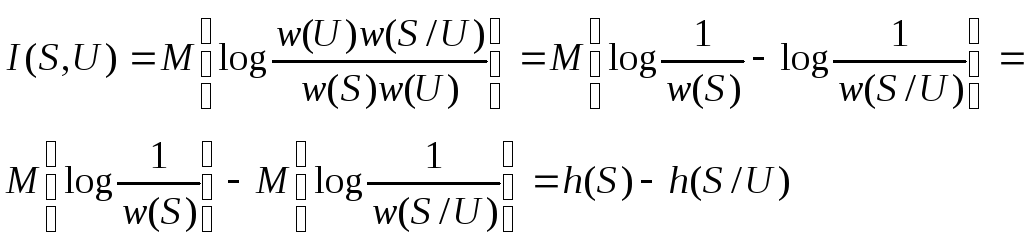(10.20)

Здесь - определённая ранее дифференциальная энтропия, а- условная дифференциальная энтропия. Легко убедиться, что основные свойства взаимной информации остаются справедливыми и в данном случае.

В качестве примера найдём дифференциальную энтропию случайной величины с нормальным распределением вероятности:

, (10.21)

где математическое ожидание, а- дисперсия.

Подставив (10.21) в (10.18), найдём:

Первый интеграл по общему свойству плотности вероятности равен 1, а второй – по определению дисперсии равен . Окончательно

(10.22)

Таким образом, дифференциальная энтропия гауссовской случайной величины не зависит от её математического ожидания и монотонно возрастает с увеличением дисперсии.

В заключение укажем одно важное свойство нормального распределения: из всех непрерывных случайных величин с одинаковой дисперсиейнаибольшую дифференциальную энтропию имеет величина с нормальным распределением.

27.. Информация в непрерывных сообщениях. Эпсилон-энтропия.

Для передачи непрерывного сообщения с абсолютной точностью нужно было бы передать бесконечно большое количество информации, что, разумеется, невозможно сделать за конечное время, пользуясь каналом с конечной пропускной способностью. Точно так же непрерывное сообщение нельзя абсолютно точно запомнить (записать) при наличии сколь угодно слабой помехи.

Тем не менее, непрерывные сообщения (например, телевизионные, телефонные) успешно передаются по каналам связи и записываются. Это объясняется тем, что на практике никогда не требуется абсолютно точного воспроизведения переданного и записанного сообщения. А для передачи даже с самой высокой, но ограниченной точностью требуется конечное количество информации так же, как и при передаче дискретных сообщений. Это количество информации тем больше, чем выше точность, с которой требуется передать (воспроизвести) непрерывное сообщение. Пусть допустимая неточность измеряется некоторым малым параметром . То минимальное количество информации, которое требуется передать по каналу связи для воспроизведения непрерывного сообщения с неточностью не более допустимой, академик А.Н.. Колмогоров предложил называть-энтропией (эпсилон-энтропией)

В дальнейшем удобнее будет оперировать не с передаваемым непрерывным сообщением А, а с первичным сигналом В и его реализациями b(t). Дело в том, что непрерывное сообщение А может и не быть функцией времени либо быть функцией нескольких аргументов (например, при телевизионном вещании). Первичный сигнал B(t) в современных системах связи всегда является функцией времени. В тех случаях, когда и сообщение является функцией времени (например, при телефонной связи), первичный сигнал B(t) точно повторяет функцию A(t) и отличается от сообщения только физической природой [например A(t) – звуковое давление, B(t) – ток]. Будем считать, что преобразование сообщения в первичный сигнал обратимо и точность воспроизведения B(t) предопределяет точность воспроизведения A(t). Поэтому в дальнейшем под сообщением будем понимать первичный сигнал В(t).

Обеспечение необходимой верности передачи является обязательным требованием к любой системе связи. При передаче дискретных сообщений верность передачи определяется вероятностью правильного приёма (или вероятностью ошибки). Такое определение верности можно распространить и на непрерывные сообщения если понятие «правильно» заменить понятием «эквивалентно». Тогда под верностью передачи непрерывных сообщений будем понимать вероятность того, что принятое сообщение эквивалентно переданному Перейдём к количественному определению -энтропии.

Минимальное количество информации, содержащееся в принятом сообщении относительно переданногоB(t), при котором они ещё эквивалентны, называется эпсилон-энтропией.

По определению

(10.36)

Рассмотрим наиболее простой случай, когда источник непрерывного сообщения (сигнала) гауссовский, то есть когда сообщение B(t) представляет собой стационарный гауссовский процесс с заданной мощностью . Поскольку, то условная дифференциальная энтропияпри заданном сообщенииB полностью определяется так называемым шумом воспроизведения (t). Поэтому . Если шум воспроизведения(t) имеет фиксированную дисперсию , то дифференциальная энтропия имеет максимум при нормальном распределении

(10.37)

При заданной дисперсии сообщения дифференциальная энтропия гауссовского источникаh(B) равна . Следовательно, эпсилон-энтропия гауссовского непрерывного источника на один отсчёт:

(10.38)

Величина 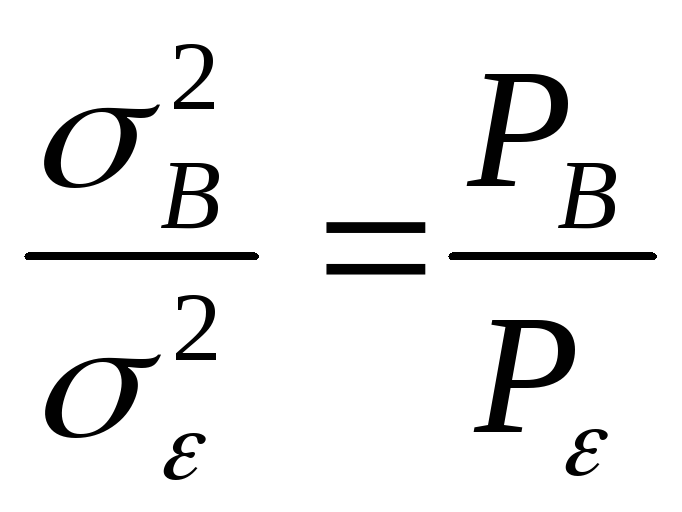характеризует минимальное отношение сигнал-шум, при котором сообщенияB(t) и ещё эквивалентны. Это отношение обычно обозначают.

Производительность непрерывных сообщений можно определить как количество информации, которое необходимо передать в единицу времени, чтобы восстановить сообщение при заданном критерии эквивалентности. Если источник выдает независимые отсчёты сообщения (сигнала) дискретно во времени со средней скоростью V, то его эпсилон-производительность:

(10.39)

Эпсилон-производительность называют также скоростью создания информации при заданном критерии верности. Для источника непрерывных сообщений, ограниченных полосой , согласно теореме Котельникова, шаг дискретизации, то есть необходимое число отсчётов в секунду равно. Если спектр сообщения в полосеравномерен, то эти отсчёты некоррелированы, а для гауссовского источника и независимы. В этом случае:

(10.40)

Подставив (10.38) в (10.40), получим для гауссового источника с равномерным спектром в полосе

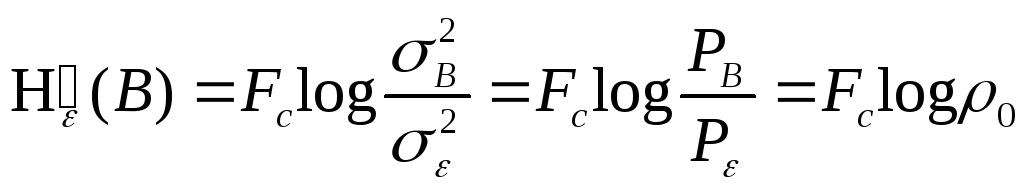(10.41)

Из предыдущих рассуждений ясно, что производительность гауссовского источника квазибелого шума (10.41) больше производительности любого другого источника с той же мощностью и той же шириной спектра при том же допустимом шуме воспроизведения , Количество информации, выдаваемое гауссовским источником за время,

(10.42)

Выражение (10.42) совпадает с характеристикой, названной объёмом сигнала, если . Это означает, что объём сигнала равен максимальному количеству информации, которая содержится в сигнале длительностью.

Для канала с пропускной способностью C, на вход которого подключён источник, обладающий производительностью , К. Шеннон доказал следующую теорему: если при заданном критерии эквивалентности сообщений источника, его эпсилон-производительность меньше пропускной способности канала, то существует способ кодирования и декодирования, при котором неточность воспроизведения сколь угодно близка к. Притакого способа не существует.

Теорема Шеннона определяет предельные возможности согласования источника непрерывных сообщений с непрерывным каналом.