
- •2.. Ортонормированный базис. Обобщенный ряд Фурье.
- •I.Свойство линейности.
- •II. Теорема о сдвигах.
- •IV.Теорема о спектре производной и неопределённого интеграла.
- •V. Теорема о свёртке.
- •VI.Теорема Планшереля
- •5.. Спектры модулированных сигналов.
- •6... Аналитический сигнал. Основные понятия и определения. Спектр аналитического сигнала
- •7… Преобразования Гильберта и его свойства. Применение преобразования Гильберта.
- •1) Преобразования Гильберта для гармонических сигналов
- •8... Автокорреляционная функция и ее свойства. Связь автокорреляционной функции и энергетического спектра сигнала.
- •9.. Взаимокорреляционная функция и ее свойства. Связь взаимокорреляционной функции и взаимного энергетического спектра.
- •10.. Дискретное преобразование Фурье. Свойства дискретного преобразования Фурье. Обратное дискретное преобразование Фурье.
- •11 Алгоритм быстрого преобразования Фурье. Число вычислительных операций. Сравнение дискретного и быстрого преобразования Фурье.
- •13.. Стационарные и эргодические случайные процессы.
- •14 ..Спектральные представления случайных процессов. Теорема Винера-Хинчина.
- •15 Белый шум и его свойства. Гауссовский случайный процесс.
- •17.. Шумоподобные сигналы и их свойства. Применение шумоподобных сигналов.
- •19.. Модуляция шумоподобных сигналов по форме и их детектирование.
- •20.. Основные положения линейной теории разделения сигналов. Структурная схема системы многоканальной передачи информации.
- •21.. Фазовое разделение сигналов.
- •22 Разделение сигналов по форме. Системы подвижной связи сдма.
- •23.. Информационные характеристики дискретных сообщений и сигналов.
- •24.. Взаимная информация и ее свойства.
- •25.. Пропускная способность каналов связи.
- •26 ..Информация в непрерывных сигналах. Дифференциальная энтропия.
- •27.. Информация в непрерывных сообщениях. Эпсилон-энтропия.
- •28.. Задача оптимального приема дискретных сообщений. Элементы теории решений.
- •29.. Критерии оптимизации приема дискретных сообщений.
- •30.. Алгоритм оптимального приема дискретных сообщений при полностью известных сигналах (Когерентный прием).
- •31.. Реализация алгоритма оптимального когерентного приема на основе корреляторов
- •33 Потенциальная помехоустойчивость оптимального когерентного приемника дискретных сообщений.
- •34.. Сравнение по помехоустойчивости систем когерентного приема с различными видами дискретной модуляции.
- •35.. Оптимальный прием дискретных сообщений с неопределенной фазой (Некогерентный прием).
- •36 Помехоустойчивость систем с различными видами дискретной модуляции при некогерентном приеме.
- •37 Прием дискретных сообщений в каналах с замираниями.
- •38 Основные принципы цифровой фильтрации
- •39 Характеристики и свойства цифровых фильтров. Алгоритм линейной цифровой фильтрации.
- •40 Трансверсальные (нерекурсивные) цифровые фильтры
- •41 Рекурсивные цифровые фильтры.
- •42 Устойчивость цифровых фильтров
- •43 Понятие вейвлет-преобразования. Основные вейвлеты, применяемые в системах связи.
- •44 Непрерывное и дискретное вейвлет-преобразования.
- •16.2 Дискретный вейвлет-анализ.
- •16.3 Непрерывное вейвлет-преобразование
1.. Основные элементы функционального анализа сигналов. Норма и метрика. Ортогональные сигналы.
Норма и метрика
Аксиомы нормированного пространства
1.
Норма неотрицательна,
т.е.
![]()
![]() .
Норма
.
Норма![]() =0
тогда и только тогда, если
=0
тогда и только тогда, если![]() В основе функционального анализа
сигналов лежит представление сигнала
как вектора, в специальным образом
сконструированном бесконечномерном
пространстве.
В основе функционального анализа
сигналов лежит представление сигнала
как вектора, в специальным образом
сконструированном бесконечномерном
пространстве.
Пусть
![]() -
множество сигналов. Причина объединения
этих объектов – наличие некоторых
свойств, общих для всех элементов
множества
-
множество сигналов. Причина объединения
этих объектов – наличие некоторых
свойств, общих для всех элементов
множества![]() .
.
Множество
сигналов
![]() образует вещественное линейное
пространство, если справедливы следующие
аксиомы:
образует вещественное линейное
пространство, если справедливы следующие
аксиомы:
Любой сигнал
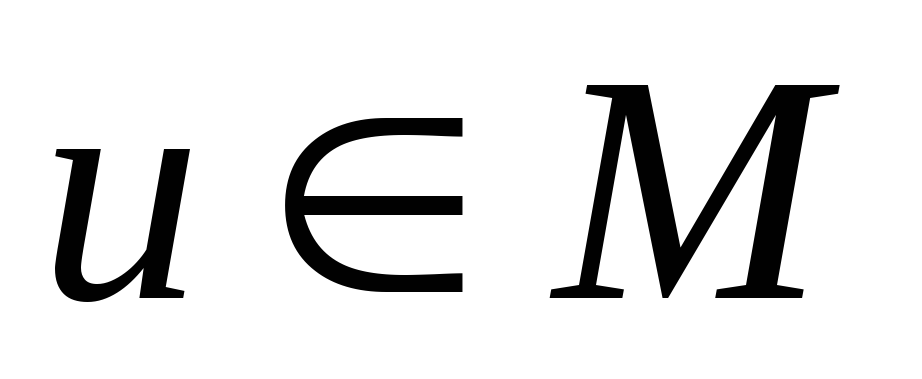 при любых
при любых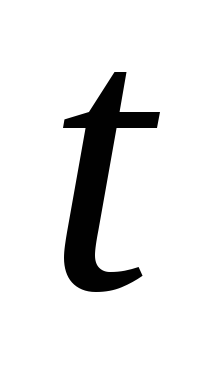 принимает лишь вещественные значения.
принимает лишь вещественные значения.Для любых
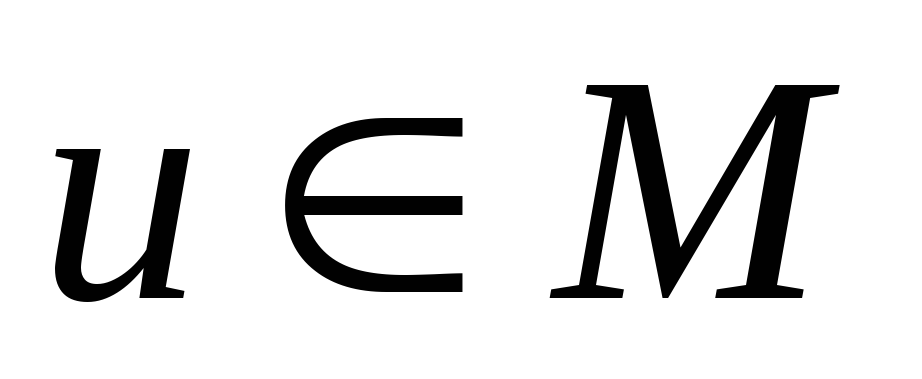 и
и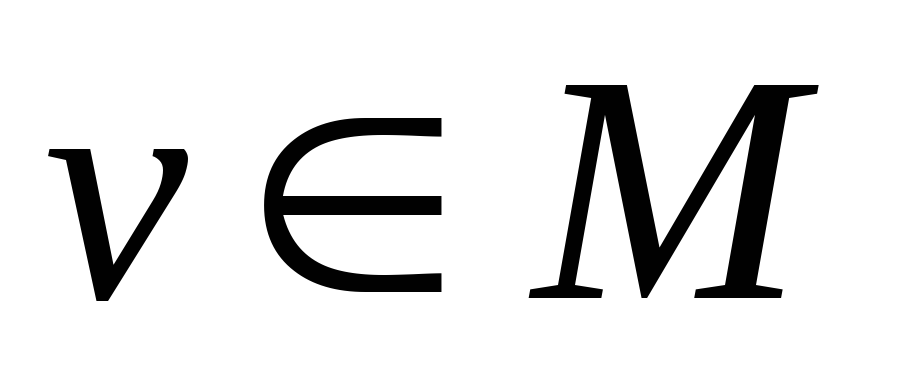 существует их сумма
существует их сумма ,
причём
,
причём также содержится в
также содержится в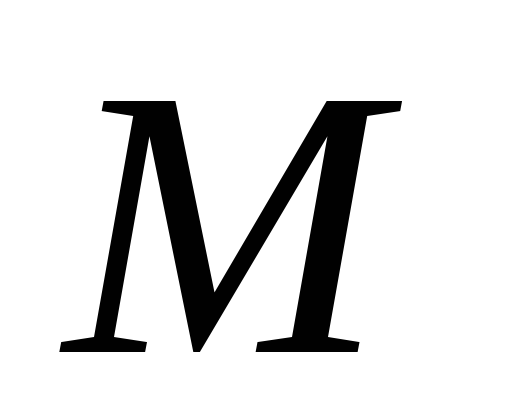 .
Операция суммирования коммутативна:
.
Операция суммирования коммутативна: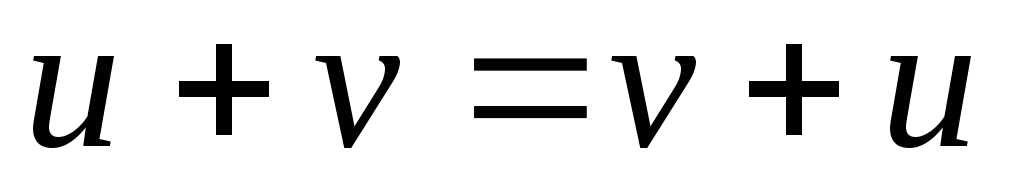 и ассоциативна
и ассоциативна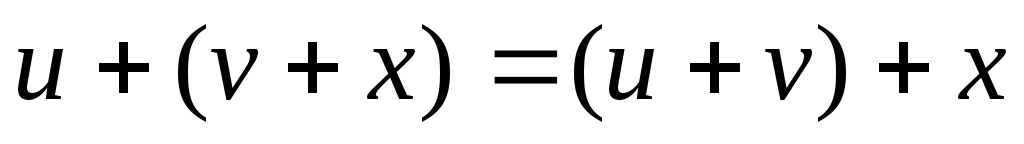 .
.Для любого сигнала
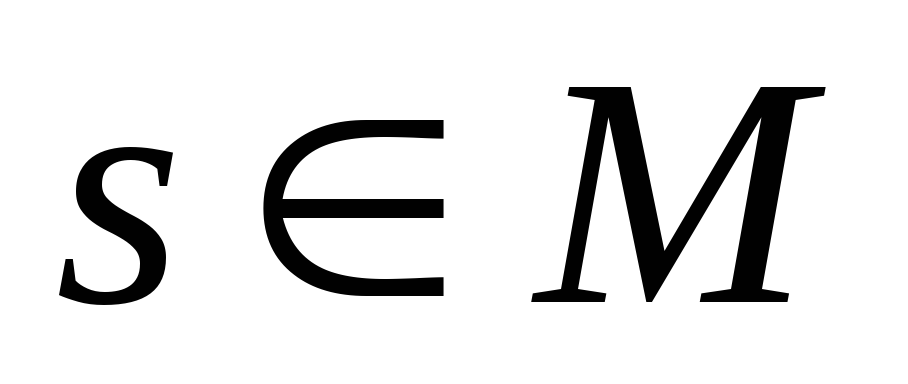 и
любого вещественного числа
и
любого вещественного числа определён сигнал
определён сигнал .
.Множество
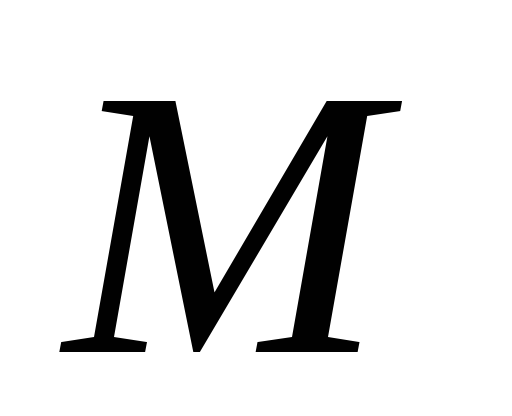 содержит особый нулевой элемент
содержит особый нулевой элемент ,
такой, что
,
такой, что для
всех
для
всех
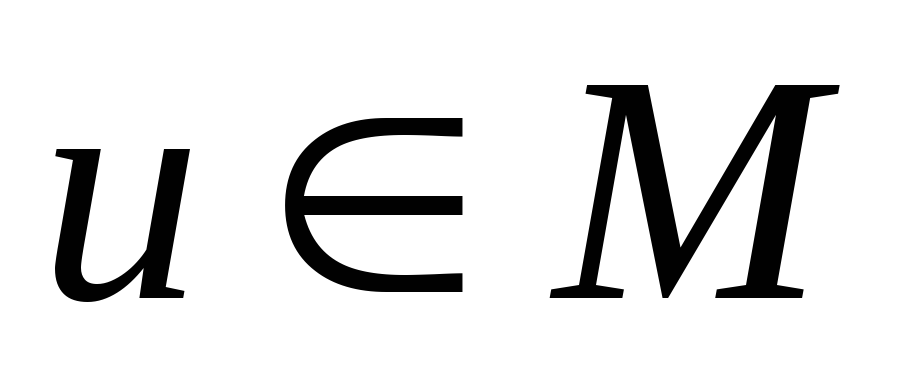 .
.
Линейное пространство, элементами которого являются функции, называется функциональным.
Если математические модели сигналов принимают комплексные значения, то, допуская в аксиоме 3 умножение на комплексное число, можем ввести понятие комплексного линейного пространства.
Совокупность
векторов
![]() ,
принадлежащих
,
принадлежащих![]() ,
является линейно независимой, если
равенство:
,
является линейно независимой, если
равенство:
![]()
возможно
лишь в случае одновременного обращения
в нуль всех числовых коэффициентов
![]() .
.
Система линейно независимых векторов образует координатный базис в линейном пространстве.
2.
Для любого числа
![]() справедливо
равенство
справедливо
равенство![]() .
.
3.
Если
![]() и
и![]() -
два вектора изL,
то выполняется неравенство:
-
два вектора изL,
то выполняется неравенство:
![]()
Существуют разные способы определения нормы сигналов. Чаще всего полагают, что вещественные аналоговые сигналы имеют норму:
![]() (из двух возможных значений корня
выбирается положительное).
(из двух возможных значений корня
выбирается положительное).
Для комплексных сигналов норма:
![]() ,
,
где *-символ комплексно-сопряжённой величины.
Квадрат нормы называется энергией сигнала
![]()
Такая
энергия выделяется в резисторе с
сопротивлением 1Ом, если на его зажимах
существует напряжение
![]() .
.
Говорят,
что линейное пространство L
становится метрическим пространством,
если каждой паре элементов
![]() сопоставлено неотрицательное число
сопоставлено неотрицательное число![]() ,
называемое метрикой, или расстоянием
между этими эле
,
называемое метрикой, или расстоянием
между этими эле
ментами. Метрика, независимо от способа её определения, должна подчиняться аксиомам метрического пространства:
Метрика рефлексивна
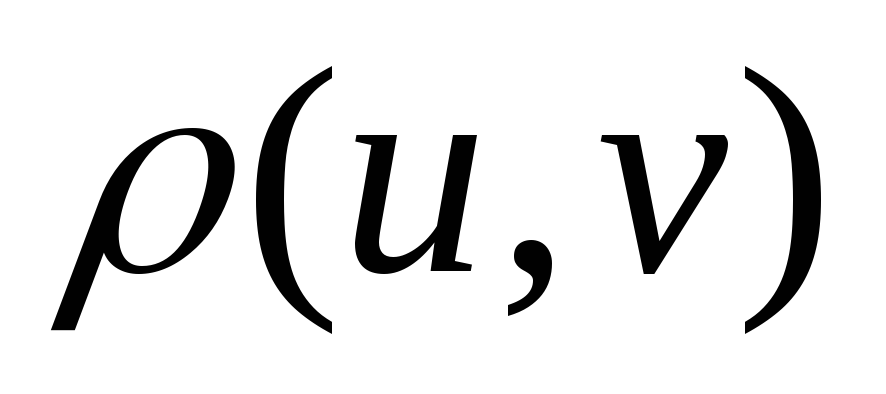 =
=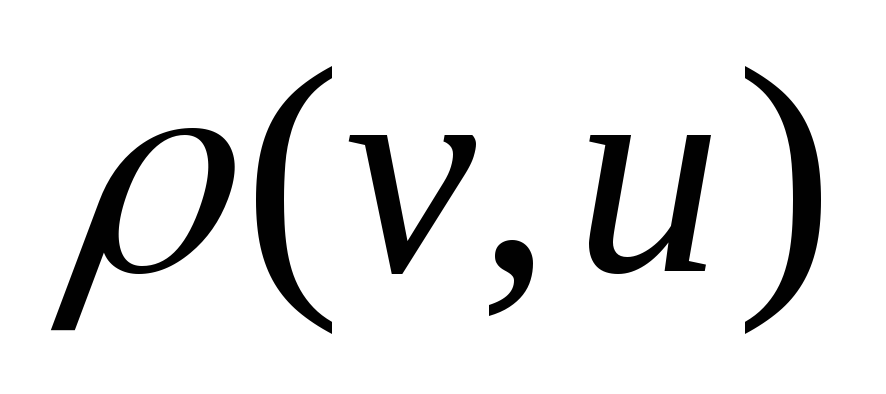
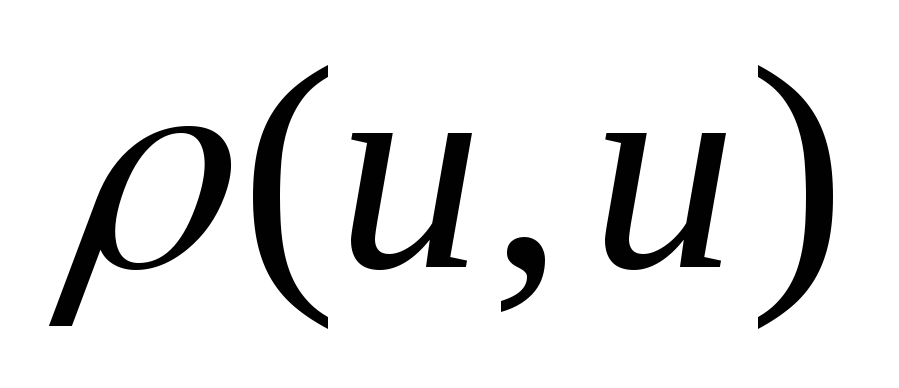 =0
при любых
=0
при любых
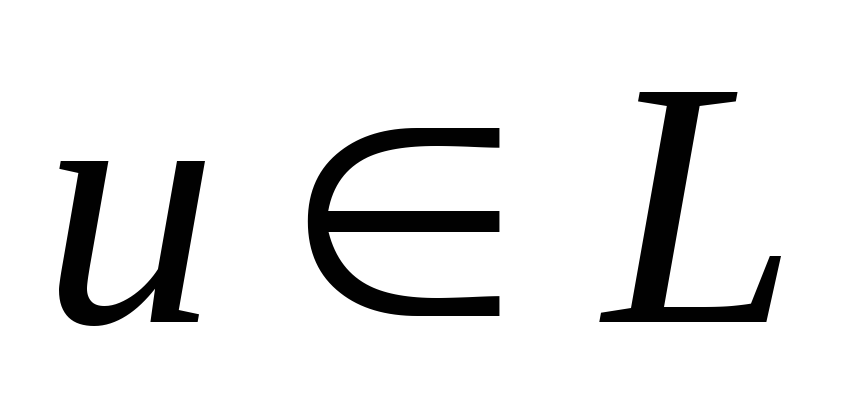 .
.Каков бы ни был элемент
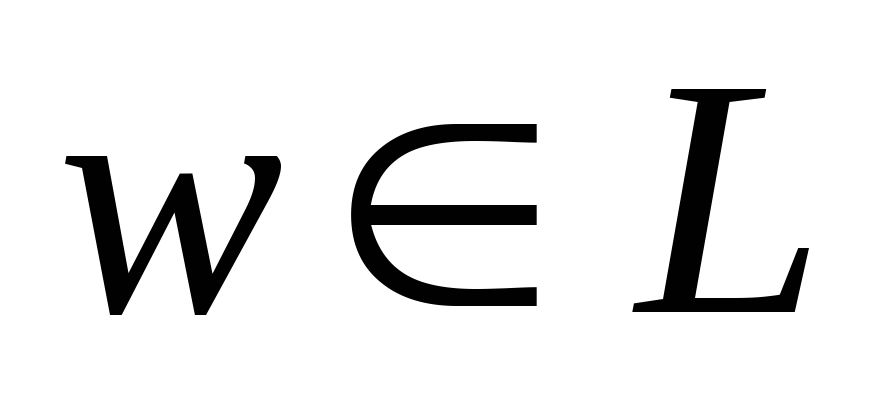 ,
всегда
,
всегда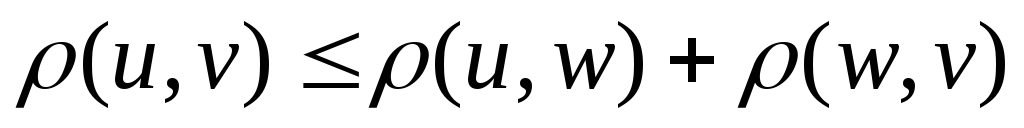 .
.
Обычно метрику определяют как норму разности двух сигналов:
![]() =
=![]()
Норму
в свою очередь, можно понимать как
расстояние между выбранным элементом
пространства и нулевым элементом:
![]() .
.
Ортогональные сигналы.
Скалярное
произведение вещественных сигналов
![]() и
и ![]() :
:
![]()
Скалярное произведение обладает следующими свойствами:
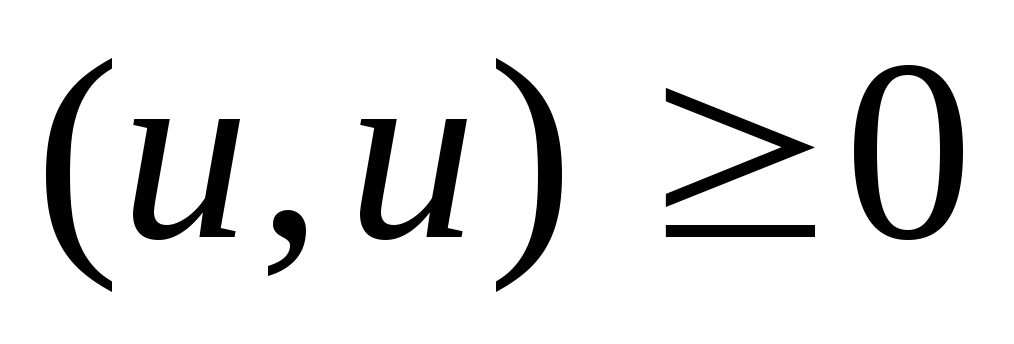
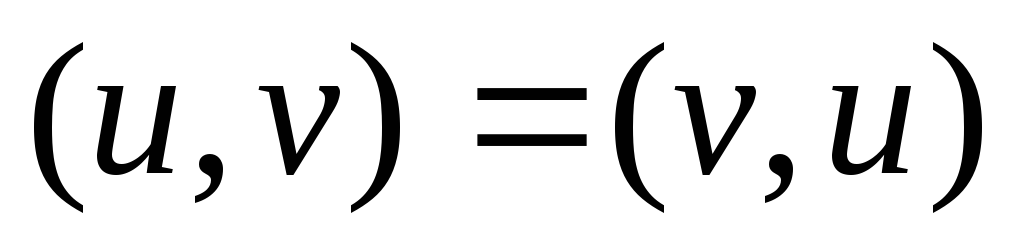
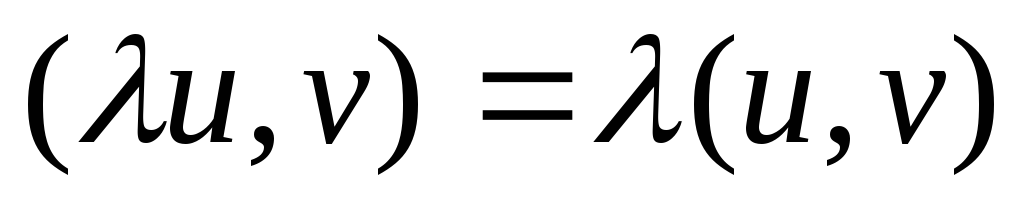 ,
где
,
где
 -
вещественное число
-
вещественное число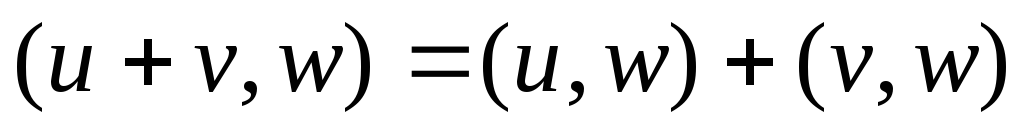
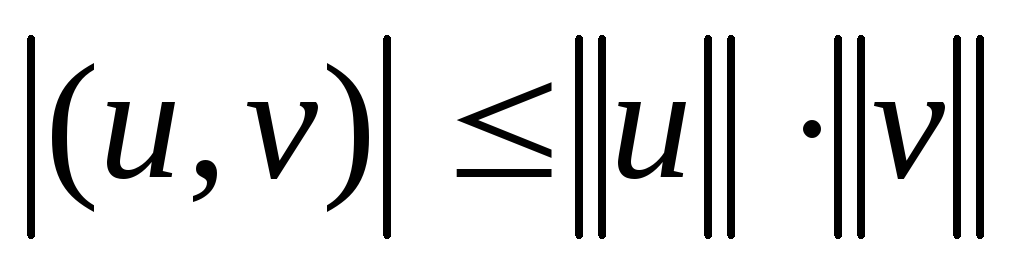 -
справедливо неравенство Коши-Буняковского.
-
справедливо неравенство Коши-Буняковского.
Линейное пространство с таким скалярным произведением, содержащее
в себе все предельные точки любых сходящихся последовательностей векторов из этого пространства называется вещественным Гильбертовым пространством H.
Если сигналы принимают комплексные значения, то можно определить комплексное Гильбертово пространство.
Если сигналы комплексные, то скалярное произведение:
![]()
Два
сигнала
![]() и
и![]() называют ортогональными, если их
скалярное произведение, а значит, и
взаимная энергия равны нулю:
называют ортогональными, если их
скалярное произведение, а значит, и
взаимная энергия равны нулю:
![]() .
.
2.. Ортонормированный базис. Обобщенный ряд Фурье.
Разложим
произвольный сигнал
![]() в ряд:
в ряд:
![]() (1.1)
(1.1)
Такое
представление называется обобщённым
рядом Фурье сигнала![]() в
выбранном базисе.
в
выбранном базисе.
Коэффициенты
данного ряда находят следующим образом.
Возьмём базисную функцию
![]() с
произвольным номером
с
произвольным номером![]() ,
умножим на неё обе части равенства (1.1)
и затем проинтегрируем результаты по
времени:
,
умножим на неё обе части равенства (1.1)
и затем проинтегрируем результаты по
времени:
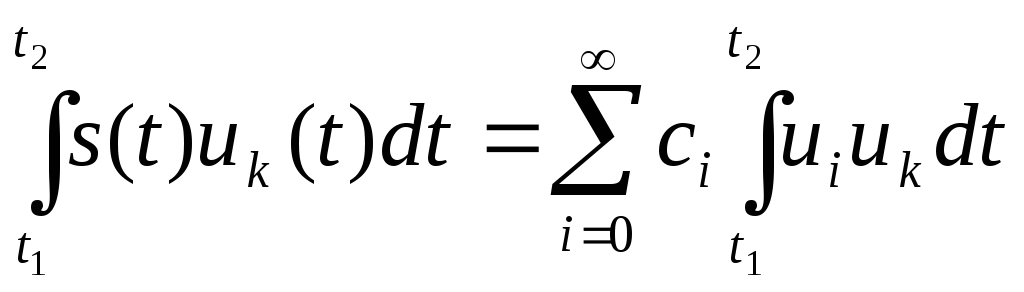 (1.2)
(1.2)
Ввиду
ортонормированности базиса по определению
в правой части равенства (1.2) останется
только член суммы с номером
![]() ,
поэтому:
,
поэтому:
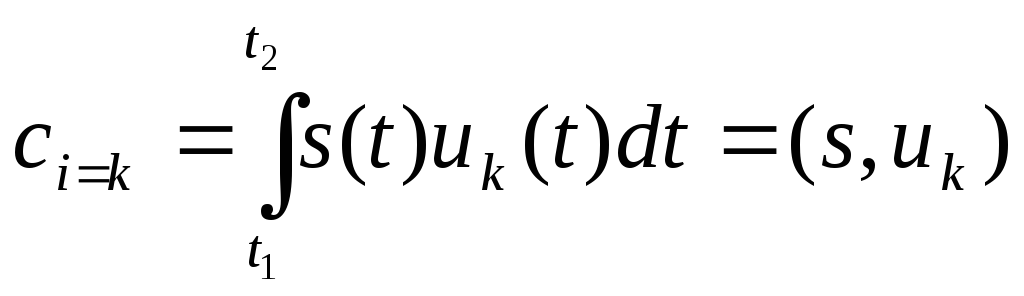 (1.3)
(1.3)
Рассмотрим
некоторый сигнал,
![]() ,
разложенный в ряд по ортонормированной
базисной системе и вычислим его энергию,
непосредственно подставив этот ряд в
соответствующий интеграл:
,
разложенный в ряд по ортонормированной
базисной системе и вычислим его энергию,
непосредственно подставив этот ряд в
соответствующий интеграл:

Поскольку
базисная система функций ортонормирована,
в сумме окажутся отличными от нуля
только члены с номерами
![]() .
Отсюда получается замечательный
результат, который называется равенством
Парсеваля:
.
Отсюда получается замечательный
результат, который называется равенством
Парсеваля:
![]() (1.4)
(1.4)
Смысл этой формулы: энергия сигнала есть сумма энергий всех компонент, из которых складывается обобщённый ряд Фурье.
3 Спектральная плотность и ее свойства. Теоремы о спектрах.
Как известно спектральная плотность и сигнал связаны между собой парой преобразований Фурье:
![]()
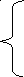 (2.1)
(2.1)
 (2.2)
(2.2)
Все свойства спектральной плотности объединены в основных теоремах о спектрах.
I.Свойство линейности.
Если
имеется некоторая совокупность сигналов
![]() причём
причём![]()
![]() ,…,
то взвешенная сумма сигналов преобразуется
по Фурье следующим образом:
,…,
то взвешенная сумма сигналов преобразуется
по Фурье следующим образом:
![]() (2.3)
(2.3)
Здесь
![]() -
произвольные числовые коэффициенты.
-
произвольные числовые коэффициенты.
II. Теорема о сдвигах.
Предположим,
что для сигнала
![]() известно соответствие
известно соответствие![]() .
Рассмотрим такой же сигнал, но возникающий
на
.
Рассмотрим такой же сигнал, но возникающий
на![]() секунд позднее. Принимая точку
секунд позднее. Принимая точку![]() за новое начало отсчёта времени, обозначим
этот смещённый сигнал как
за новое начало отсчёта времени, обозначим
этот смещённый сигнал как![]() .
Введём замену переменной:
.
Введём замену переменной:![]() .
Тогда
.
Тогда![]() ,
,![]()
 (2.4)
(2.4)
Модуль
комплексного числа
![]() при любых
при любых![]() равен 1, поэтому амплитуды элементарных
гармонических составляющих, из которых
складывается сигнал, не зависят от его
положения на оси времени. Информация
об этой характеристике сигнала заключена
фазовом спектре.
равен 1, поэтому амплитуды элементарных
гармонических составляющих, из которых
складывается сигнал, не зависят от его
положения на оси времени. Информация
об этой характеристике сигнала заключена
фазовом спектре.
III. Теорема масштабов.
Предположим,
что исходный сигнал
![]() подвергнут изменению масштаба времени.
Это означает, что роль времени
подвергнут изменению масштаба времени.
Это означает, что роль времени![]() играет новая независимая переменная
играет новая независимая переменная![]() (
(![]() -
некоторое вещественное число.) Если
-
некоторое вещественное число.) Если![]() >
1, то происходит “ сжатие” исходного
сигнала; если же 0<
>
1, то происходит “ сжатие” исходного
сигнала; если же 0<![]() <1,
то сигнал “растягивается” во времени.
Если
<1,
то сигнал “растягивается” во времени.
Если![]() ,
то :
,
то :
![]() (2.5)
(2.5)
При
сжатии сигнала в
![]() раз на временной оси во столько же раз
расширяется его спектр на оси частот.
Модуль спектральной плотности при этом
уменьшается в
раз на временной оси во столько же раз
расширяется его спектр на оси частот.
Модуль спектральной плотности при этом
уменьшается в![]() раз.
раз.
Очевидно,
что при растягивании сигнала во времени
( т.е. при
![]() <1)
имеет место сужение спектра и увеличение
модуля спектральной плотности.
<1)
имеет место сужение спектра и увеличение
модуля спектральной плотности.
IV.Теорема о спектре производной и неопределённого интеграла.
Пусть
сигнал
![]() и его спектральная плоскость
и его спектральная плоскость![]() заданы. Будем изучать новый сигнал
заданы. Будем изучать новый сигнал![]() и поставим цель найти его спектральную
плотность
и поставим цель найти его спектральную
плотность![]() .
.
По определению:
![]()
Преобразование Фурье – линейная операция, значит, равенство (2.3) справедливо и по отношению к спектральным плотностям. Получаем по теореме о сдвигах:
находим
![]()
![]() (2.7)
(2.7)
Итак,
дифференцирование сигнала по времени
эквивалентно простой алгебраической
операции умножения спектральной
плотности на множитель
![]() .
Поэтому говорят, что мнимое число
.
Поэтому говорят, что мнимое число![]() является оператором дифференцирования,
действующим в частотной области.
является оператором дифференцирования,
действующим в частотной области.
Вторая
часть теоремы. Рассмотренная функция
![]() является неопределённым интегралом по
отношению к функции
является неопределённым интегралом по
отношению к функции![]() .
.
![]() (2.8)
(2.8)
Таким
образом, множитель
![]() служит оператором интегрирования в
частотной области.
служит оператором интегрирования в
частотной области.
