2.5. Примеры исследования динамики нелинейных систем

2.5.1. Исследование нелинейной следящей системы с двухпозиционным реле с зоной неоднозначности

На рис. 2.18 приведена упрощенная схема исследуемой системы.

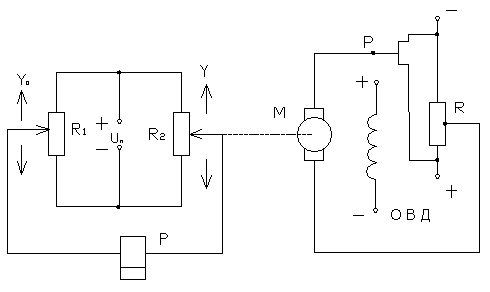
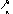
Рис. 2.18. Функциональная схема следящей системы с двухпозиционным реле с зоной неоднозначности

При перемещении движка реостата R₁(задатчика) мост разбалансируется и через обмотку поляризованного релеPначнет протекать ток, что вызовет замыкание контактов этого реле в цепи якоря двигателяM, который начнет вращаться и переместит движок датчикаR₂, стремясь восстановить равновесие моста. Таким образом, движокR₂«следит» за движкомR₁.

Структурная схема следящей системы с двухпозиционным реле с зоной неоднозначности представлена на рис. 2.19.

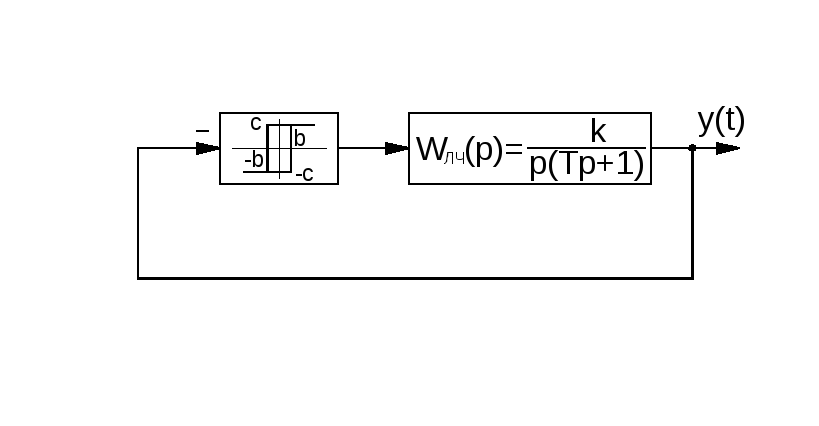
Рис. 2.19. Структурная схема следящей системы с двухпозиционным реле с зоной неоднозначности

На этой схеме: y₀– задающее воздействие;y(t) – регулируемая величина.

Нелинейный элемент (поляризованное реле) имеет характеристику, приведенную на рис. 2.20.

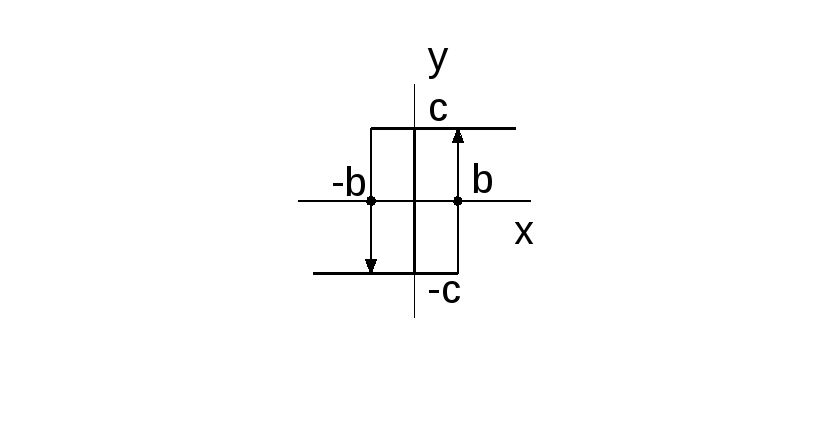
Рис. 2.20. Статическая характеристика поляризованного реле

Пусть параметры системы таковы:

• электромеханическая постоянная времени двигателя T = 0,1 с (электромагнитной постоянной времени пренебрегаем);

• коэффициент передачи линейной части K = 10 рад/В;

• параметры нелинейного элемента (см. рис. 2.20) b = 5, c = 1.

Коэффициенты гармонической линеаризации для реле с заданной характеристикой определяются следующим образом

,приA  b.

Уравнение гармонического баланса

.

Частотная функция линейной части

,

где действительная часть

,

а мнимая часть

.

Обратная инверсная частотная функция нелинейного элемента, полученная в результате гармонической линеаризации, после достаточно громоздких преобразований

,

где действительная часть

,

мнимая часть

.

Можем записать V() = V(A), или

,

откуда

или

.

После подстановки числовых значений параметров получим уравнение

,

действительный корень которого дает частоту автоколебаний _a = 2,407 рад/с  2,41 рад/с.

Запишем уравнение гармонического баланса в другом виде

.

Здесь

;

.

Можно записать , т.е.

,

откуда амплитуда автоколебаний

.

Эту же задачу можно решить графоаналитическим методом, построив АФХ линейной части и АФХ нелинейного элемента. Точка пересечения характеристик соответствует искомым параметрам автоколебаний (рис. 2.21).

Рис. 2.21. К определению параметров автоколебаний графоаналитическим методом

Модель исследуемой системы в Simulink приведена на рис. 2.22.

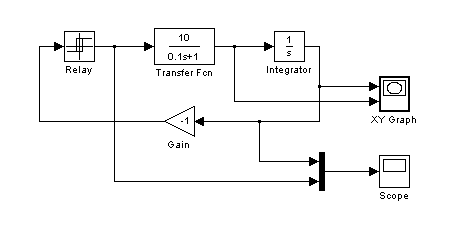
Рис. 2.22. Модель НС с двухпозиционным реле с зоной неоднозначности в Simulink

Н

y(t)

y₁

а рис. 2.23 показаны график переходного процессаy(t) с переключениями релейного элемента фазовая траектория следящей системы.

t а)

y б)

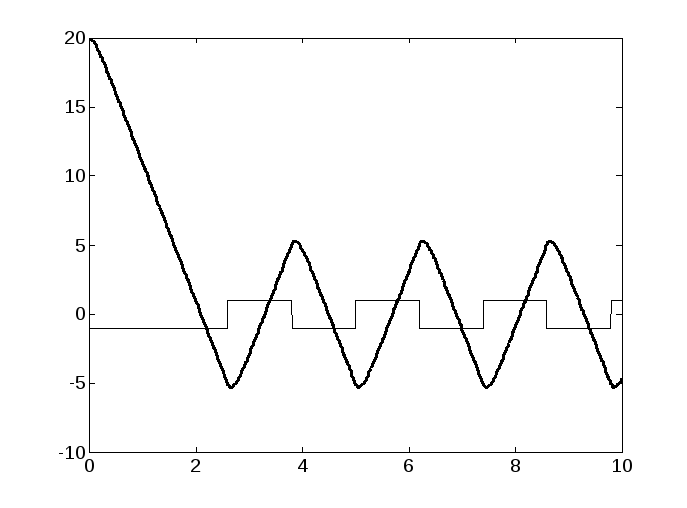
Рис. 2.23. Результаты моделирования НС с двухпозиционным реле: а) график переходного процесса; б) фазовая траектория

Период колебаний T_k = 2,45 с. Частота колебанийрад/с, а амплитудаA  5,14, что практически совпадает с результатами расчета.

2.5.2. Исследование релейной аср в скользящем режиме

Рассмотрим нелинейную следящую систему, описанную в разд. 2.4, в которой исполнительным устройством является электрический двигатель, а регулятор представляет собой идеальное реле (рис. 2.14).

Пусть, например, передаточная функция замкнутого контура скорости

,

где Т = 0,14 с;  = 0,707; K = 3,75.

Регулятор (идеальное реле) характеризуется параметром с = 10.

После очевидных преобразований передаточная функция замкнутой системы

,

а характеристическое уравнение

или

,

где a₃ = T² = 0,142 = 0,0196;

a₂ = 2T = 2  0,707  0,14 = 0,198;

a₁ = 1;

a₀ = K  q = 3,75  q.

Для возникновения автоколебаний, как уже указывалось, необходимо наличие чисто мнимого корня p = j

.

Действительная и мнимая части

;

.

Из уравнения V() = 0 может быть определена частота автоколебаний

с^-1.

Период колебаний

с.

Теперь из уравнения U() = 0 с учетом  = _а можно определить амплитуду автоколебаний

.

Для обоснования справедливости применения метода гармонической линеаризации необходимо проверить гипотезу фильтра. Для этого найдем значения АЧХ линейной части системы на частотах _а и 2_а (вторая гармоника).

АЧХ линейной части можно представить в виде

,

где А₁() и А₂() – АЧХ колебательного и интегрирующего звеньев

.

После подстановки численных значений параметров получим А(_а) = 0,32, А(2_а) = 0,058. Так как А(2_а) << А(_а), можно считать, что ЛЧ практически не пропускает высшие гармоники и, таким образом, является фильтром нижних частот, а применение метода гармонической линеаризации справедливо.

Для проверки найденного периодического режима на устойчивость применим к характеристическому уравнению критерий устойчивости Гурвица. Для системы третьего порядка при положительности всех коэффициентов условие устойчивости сводится к выполнению неравенства

, (2.14)

которое при A(t) = А₀ должно принять вид равенства

.

Подставив в уравнение U() = 0, получим

или

. (2.15)

Левая часть неравенства (2.14) отличается от выражения (2.15) только значением a₀ = K  q, так какв первом случае коэффициент гармонической линеаризации , а во втором –.

При A(t) = A₀ неравенство (2.14) обращается в равенство.

При A(t) > A₀ неравенство (2.14) выполняется, и величина A(t), уменьшаясь, стремиться к A₀.

При A(t) < A₀ неравенство (2.14) не выполняется, величина A(t) возрастает, стремясь к A₀ и оставаясь меньше ее. Следовательно, найденное решение устойчиво, и в системе наблюдаются автоколебания.

Оценить значение , обеспечивающегоА₀ < А_задможно из характеристического уравнения системы с учетом дополнительной обратной связи по производной. При этом ; . Для рассматриваемого случая_а = 21,97 с^-1; = 0,089.

Модель АСУ в Simulink приведена на рис. 2.24. В ней предусмотрена возможность введения обратной связи по производной. При  = 0 эта связь отсутствует.

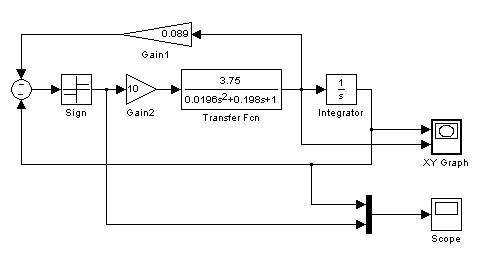
Рис. 2.24. Схема моделирования скользящего режима в Simulink

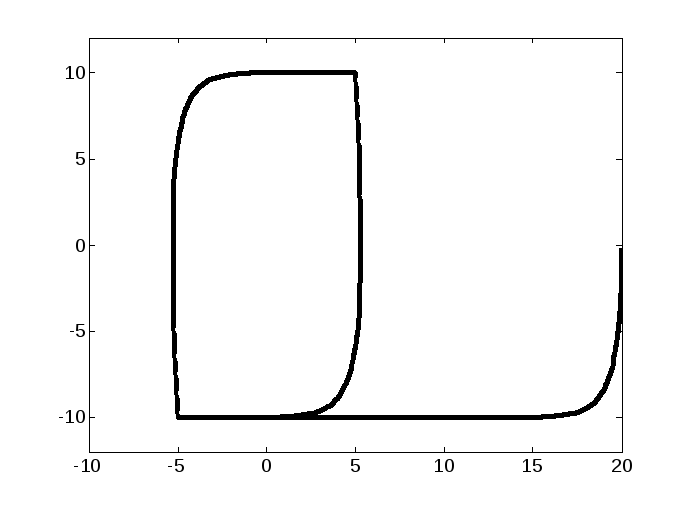
На рис. 2.25, а представлены графики переходного процесса для выходной переменной (t) и переключения релеz(t), из которых видно, что амплитуда и частота автоколебаний совпадает с расчетными. На фазовой плоскости (рис. 2.25, б) фазовыетраектории сходятся к замкнутому устойчивому предельному циклу, определяющему параметры автоколебаний.

y(t)

y₁

t а)

y б)

Рис. 2.25. Результаты моделирования скользящего режима в НС без обратной связи по производной: а) график переходного процесса; б) фазовая траектория

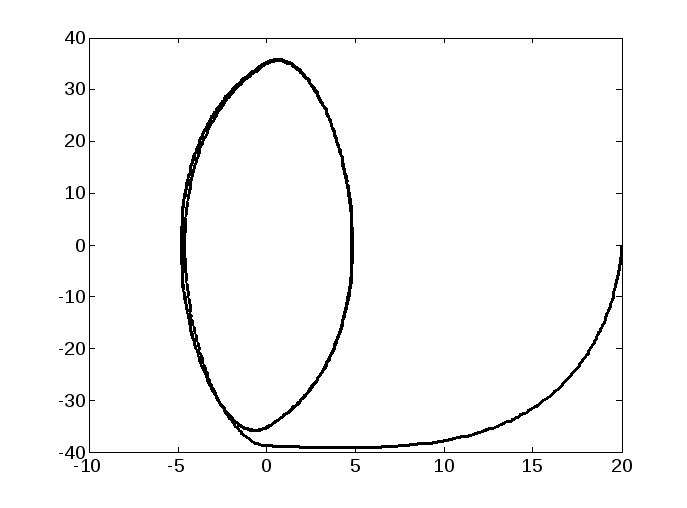
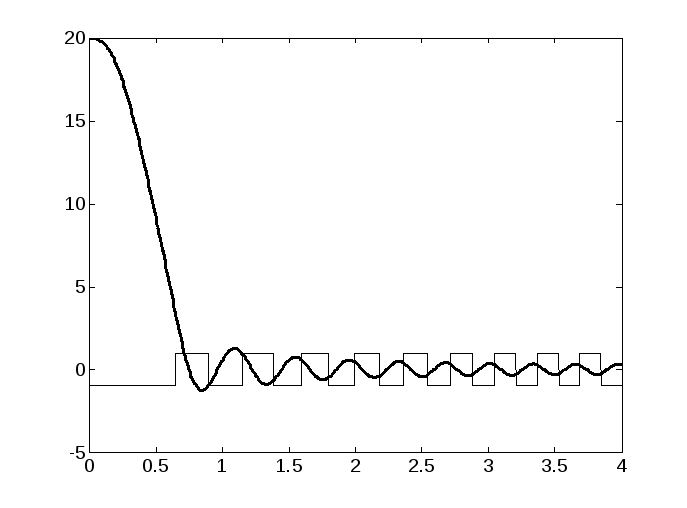
При введении обратной связи по производной картина изменяется (см. рис. 2.26). Амплитуда колебаний уменьшается и в пределе при t   стремится к нулю, а частота колебаний увеличивается.

y(t)

y₁

t а)

y б)

Рис. 2.26. Результаты моделирования скользящего режима в НС с обратной связью по производной: а) график переходного процесса; б) фазовая траектория