2. Динамика нелинейных систем

Существует достаточно распространенный класс НС, характеризуемый тем, что систему можно представить в виде соединения двух частей – линейной ЛЧ и нелинейного элемента НЭ. Линейная часть описывается, как известно, обыкновенными дифференциальными уравнениями с постоянными коэффициентами, а статическая нелинейность – нелинейной зависимостью x=f(y) (рис. 2.1).

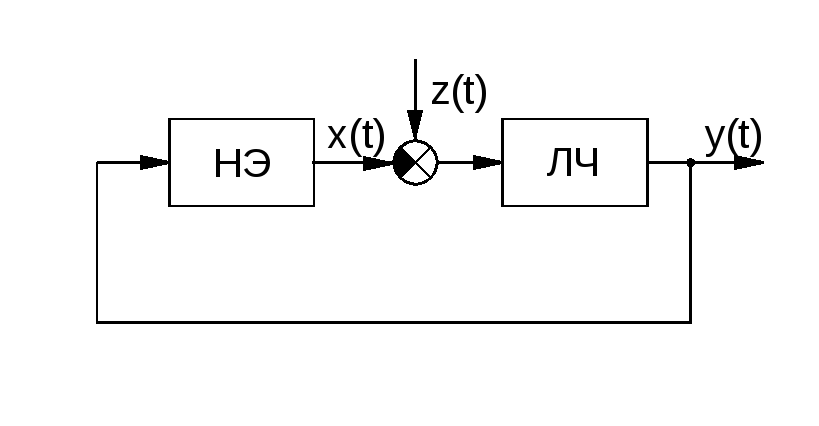
Рис. 2.1. Представление нелинейной системы в виде соединения линейной части (ЛЧ) и нелинейного элемента (НЭ)

Путем эквивалентных преобразований соединение нескольких нелинейных элементов можно заменить одним по правилам, изложенным в предыдущем разделе.

2.1. Исследование нелинейных систем методом фазовой плоскости

Дифференциальное уравнение замкнутой системы n-го порядка можно преобразовать в системуnдифференциальных уравнений первого порядка:

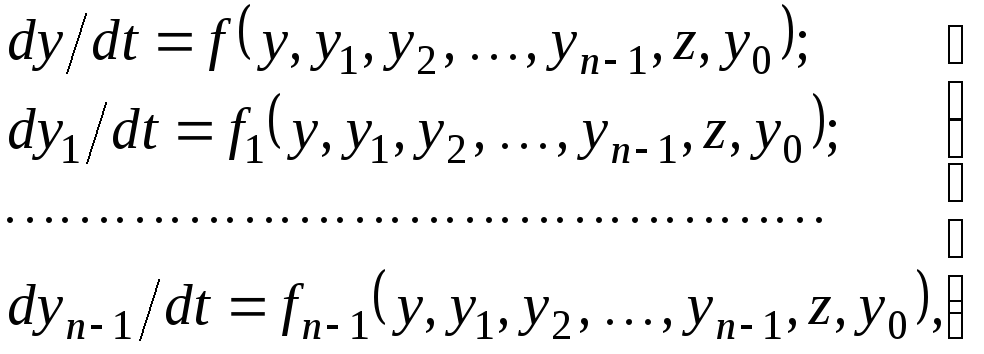
где y – управляемая переменная; z – возмущение; y₀ – задающее воздействие; y₁, y₂, …, y_n-1 – вспомогательные переменные.

Например, система третьего порядка будет иметь три переменные: y,y₁,y₂. Эти переменные можно представить в виде прямоугольных координат некоторой точкиM, характеризующей состояние системы. В процессе управления точкаMперемещается по определенной траектории. Эта траектория служит иллюстрацией поведения системы (см. рис. 2.2).

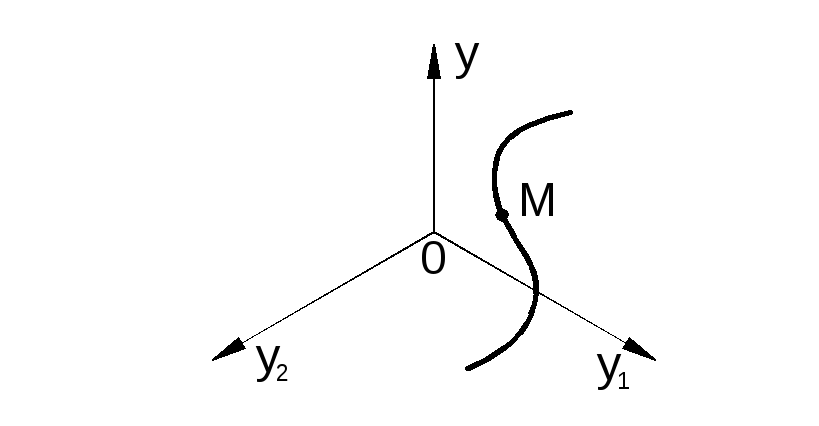
Рис. 2.2. Фазовое пространство системы третьего порядка

Пространство (y,y₁,y₂) называютфазовым пространством, точкуM– изображающей точкой, а ее траекторию – фазовой траекторией. Совокупность фазовых траекторий, полученных при различных начальных условиях, образуетфазовый портрет.

Наиболее часто используют две фазовые переменные: основную координату yи скорость ее измененияy₁ = dy / dt. В этом случае при измененииtизображающая точка перемещается пофазовой плоскости, прочерчиваяфазовую траекторию. На траектории можно отметить положение изображающей точки в моментыt₀,t₁,t₂, … и таким образом ввести переменнуюtв изображение движения (рис. 2.3).

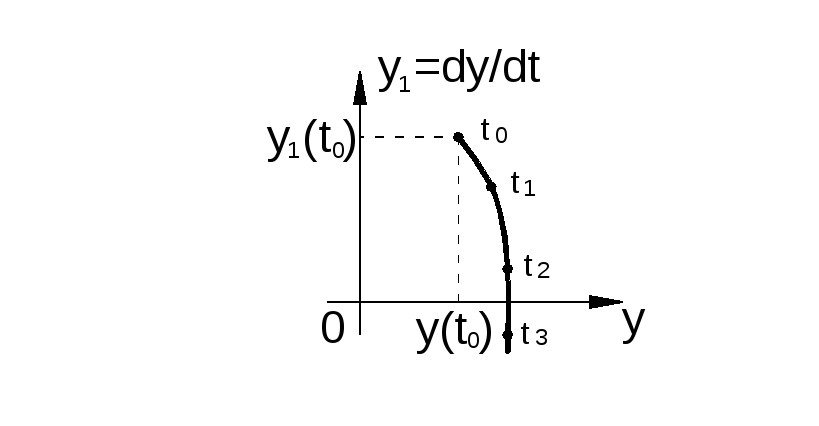
Рис. 2.3. Фазовая плоскость

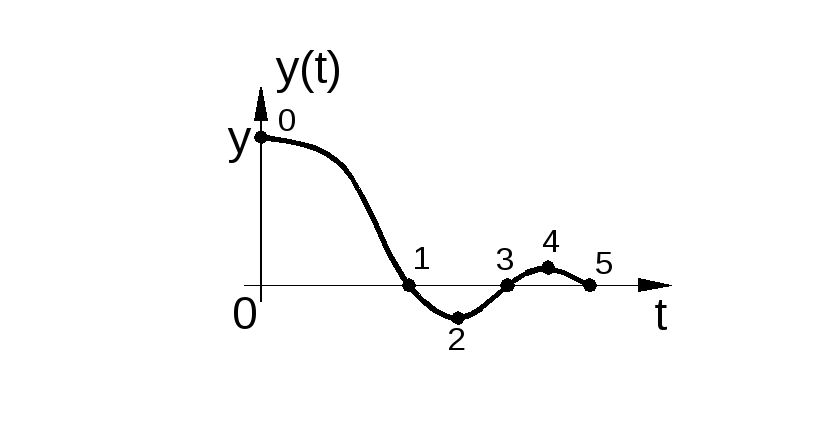
На рис. 2.4 показан пример переходного процесса, вызванного в устойчивой системе изменением задающего воздействия (рис.2.4, а), и его изображение на фазовой плоскости (рис.2.4, б).

а)

б)

Рис. 2.4. Переходной процесс (а) и фазовая траектория (б) в устойчивой системе при изменении задающего воздействия

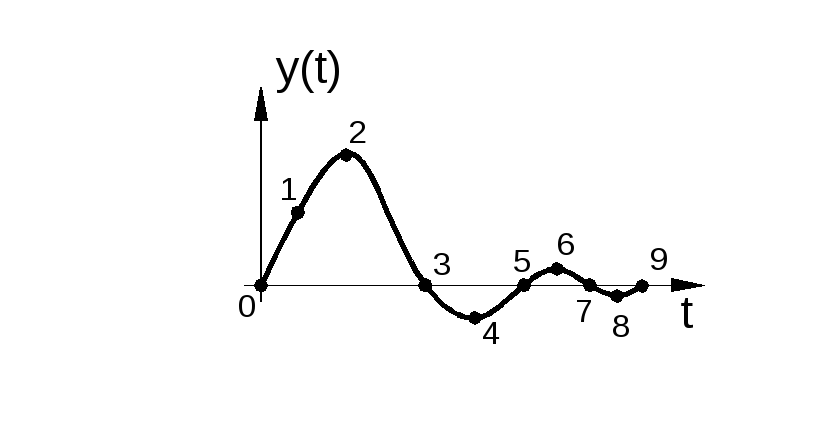
Те же характеристики для случая, когда переходной процесс в устойчивой системе возникает из-за изменения возмущения приведены на рис. 2.5.

а)

б)

Рис. 2.5. Переходной процесс (а) и фазовая траектория (б) в устойчивой системе при изменении возмущения

Метод фазовой плоскости является основным методом исследования нелинейных систем второго порядка. Для таких систем построение фазового портрета можно выполнить непосредственно по дифференциальному уравнению, не решая его. Для этого сначала необходимо свести описание системы к двум уравнениям первого порядка

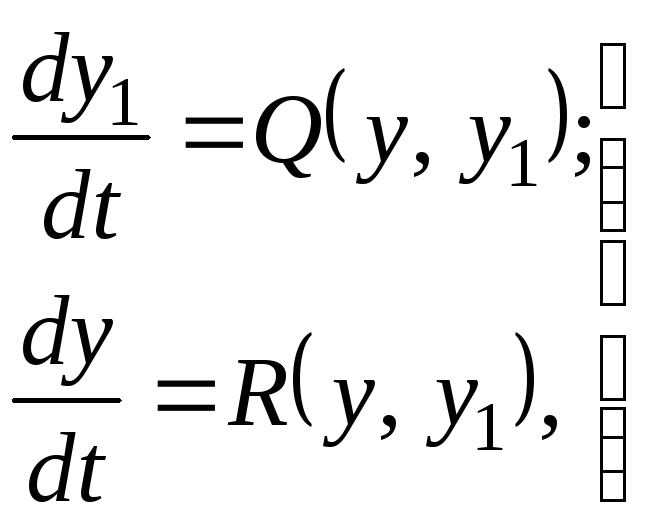(2.1)

где QиR– нелинейные функции от выходной величины yи ее производнойy₁.

Разделив первое уравнение системы (2.1) на второе, получим уравнение фазовых траекторий

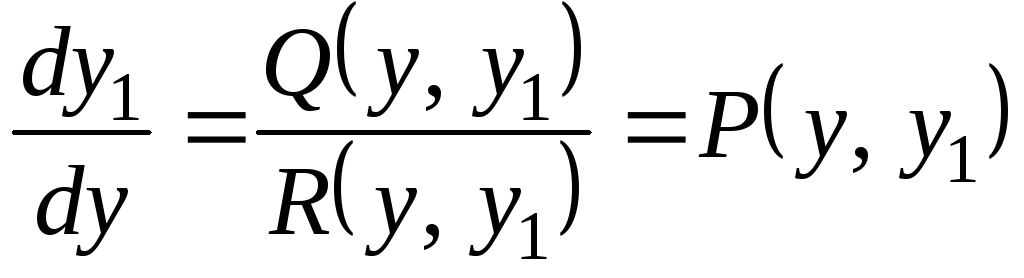, (2.2)

являющееся нелинейным дифференциальным уравнением первого порядка.

Проинтегрировав (2.2), можно по точкам построить фазовую траекторию. Если интегрирование затруднено, можно применить приближенные методы, позволяющие получить качественную картину фазовых траекторий. Одним из таких методов является метод изоклин.

Изоклиной называется такая линия, которую разные фазовые траектории пересекают под одним и тем же углом к оси абсцисс.

Для получения уравнений изоклин нужно принять

, (2.3)

где c– определенный тангенс угла наклона фазовых траекторий к оси абсцисс.

Рис. 2.6. Построение фазовых траекторий методом изоклин

Задаваясь различными значениями c, строят семейство изоклин (сплошные линии на рис. 2.6). На каждую изоклину наносятся стрелки под углом=arctg cк оси абсцисс. Соединяя эти стрелки плавной кривой (пунктир на рис. 2.6), получают искомые фазовые траектории.

Изучение фазовых портретов позволяет выявить характерные особенности анализируемых систем. На рис. 2.7 показан случай, когда при любых начальных значениях yсистема приходит в состояние равновесия. Однако этому состоянию соответствует не одна точка фазовой плоскости, а отрезок прямой на оси абсцисс, длина которого зависит от величины зоны нечувствительности системы.

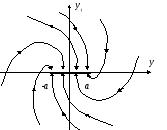
Рис. 2.7. Фазовый портрет устойчивой системы с зоной нечувствительности

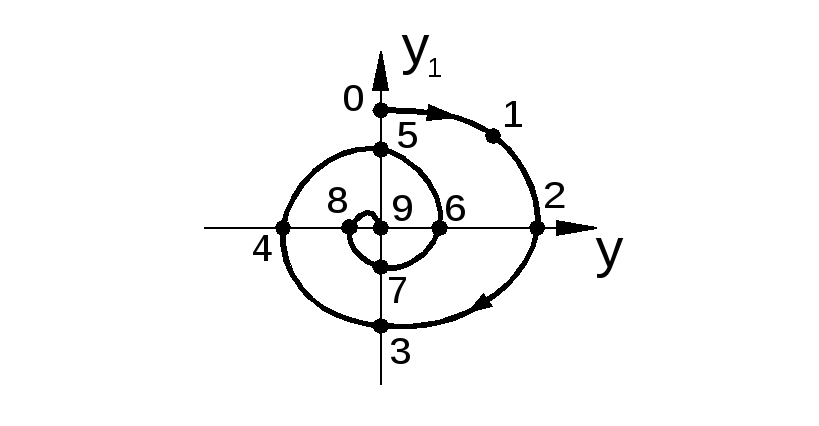
На рис. 2.8 показан фазовый портрет системы, устойчивой «в малом» и неустойчивой «в большом». Эти области разграничиваются замкнутым контуром, который свидетельствует о наличии неустойчивого периодического режима.

На рис. 2.9 показан фазовый портрет системы, где фазовые траектории при малых отклонениях асимптотически приближаются к некоторому замкнутому контуру. К этому же контуру сходятся и траектории, начинающиеся вне его. Этот контур называют предельным циклом. Он свидетельствует о наличии в системе автоколебаний, которые в общем случае не являются синусоидальными, как это имеет место в линейных системах. Отметим, что автоколебания не порождаются внешними периодическими воздействиями, а отражают внутренние свойства нелинейной системы. При этом амплитуда автоколебаний в НС не зависит от внешнего воздействия и от начальных условий. Допустим, что автоколебания имеют вид синусоиды

.

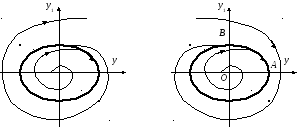
Рис. 2.8. Фазовый портрет системы устойчивой «в малом» и неустойчивой «в большом»

Рис. 2.9. Фазовый портрет автоколебательной системы

Амплитуда автоколебаний равна отрезку ОАна оси абсцисс, а так как

,

то при отрезокOBравени, таким образом, частота автоколебаний равна отношению отрезков

.

Отметим некоторые важные особенности фазовых портретов:

1. Так как при y₁ = dy / dt > 0 координата y может только возрастать, то в верхней полуплоскости фазовой плоскости при возрастании t изображающая точка движется слева направо, а в нижней справа налево (направление движения отмечают стрелками).

2. В точках, где y₁ = 0, а f(y, y₁)  0 фазовые траектории пересекают ось абсцисс под прямым углом.

3. Точки, где y₁ = 0, f(y, y₁) = 0 называются особыми. Решение системы уравнений y₁ = 0, f(y, y₁) = 0 дает значения абсцисс точек равновесия системы. В нелинейных системах часть этих точек может соответствовать устойчивым, а часть неустойчивым состояниям равновесия.