7.2 .Задача отыскания кратчайшего расстояния в сети между парами вершин

Постановка задачи. Пусть задан ориентированный графG=E,V,H, в котором для каждой дугиvVзадана длинас_v.На множестве вершинE выделены две вершиныник (соответственно начало и конец пути). Требуется среди всех путей

н=i₀, v₁, i₁, v₂, i₂,..., v_k, i_k=к, соединяющих вершиныtиs, гдеh₁(v_j)=i_j–1, h₂(v_j)=i_j , j=1,2,3,…,k, с длиной, определить путь, длина которого минимальна.

На графе, изображенном на этом рисунке, выделено 2 пути из вершины 1 в вершину 9: путь 1 – 1, v₂, 4, v₉,7, v₁₆, 9,

путь 2 – 1, v₁, 3,v₇, 5,v₁₂, 6, v₁₄, 9.

Если считать, что длины всех дуг равны 1, то длина первого пути равна 3, длина второго пути равна 4. Не трудно видеть, что длина кратчайшего пути равна 3, и кратчайший путь не единственный.

Алгоритм Беллмана – Калабы

Обозначим через W_iдлину кратчайшего пути от вершиныiдо вершинык. Согласно принципа оптимальности Беллмана

Значение W_нбудет длиной кратчайшего пути от вершинындо вершинык. Для кратчайшего путин=i₀, v₁, i₁, v₂, i₂,..., v_k, i_k=ксправедливо равенство . Алгоритм Белмана–Калабы представляет собой аналог метода простой итерации. Начальное приближение имеет вид

Первый этап.

0–шаг(задание начального приближения). , гдеM – достаточно большое число, например заведомо большее, чем длина самого длинного пути.

j–ый шаг. ( j=1,2,3,...)

Если после двух следующих друг за другом итерациях jи (j+1)для всехiE, то полагаем для всехiE . ЕслиW_н  M, то задача не имеет решения (нет путей между вершинаминик), в противном случае переходим к выполнению второго этапа.

Второй этап.

0–шаг. Положить.

j–ый шаг(j=1,2,3,...)

Положить ,

Если , то алгоритм прекращает работу, в противном случае переходим к следующему шагу.

Пример.Пусть граф имеет следующий вид:

Для него длины дуг заданы в таблице:

дуга	v1	v2	v3	v4	v5	v6	v7	v8	v9	v10
длина	3	3	1	1	2	4	1	1	5	1

Эти длины также записаны на графе рядом с дугами.

Шаг 0. Заполнения столбца «шаг 0» очевидно.

	шаг 0
вершина	W0
1	¥
2	¥
3	¥
4	¥
5	¥
6	0

Значения поместим в граф рядом с вершинами

Шаг 1. Заполнение клетки (6, шаг 1) очевидно. Вычислим , в клетку (1, шаг 1) вносим (,–). Далее вычислим, минимум достигается на дугеv₆. И так далее, получим значения остальных клеток шага 1.

	шаг 0	шаг 1
вершина	W0	W1	v
1	¥	¥	–
2	¥	4	v6
3	¥	¥	–
4	¥	5	v9
5	¥	1	v10
6	0	0	–

Жирным выделены дуги, на которыхдостигается минимум при вычислении W¹.

Выполняя аналогичным образом 4 шага получим

	шаг 4	шаг 5
вершина	W4	(W5,v)
1	4	(4,v3)
2	3	(3,v4)
3	2	(2,v7)
4	2	(2,v8)
5	1	(1,v10)
6	0	(0,–)

Для восстановления оптимального пути используем столбец шага 2, движение начинаем из вершины 1, для нее запомнена дуга v₃. По этой дуге попадаем в вершину 2, из вершины 2 по дуге v₄в вершину 4, т.д. Таким образом, оптимальный путь следующий (1,v₃ ,2,v₄ ,4,v₈ ,5,v₁₀ ,6), его длина равна.

Алгоритм Флойда.

Пусть W_i – верхние оценки кратчайших расстояний от вершиныiдо вершинык, для самой вершиныкW_к=0. Если для всех дугvVвыполняется, то оценкиW_iдают кратчайшие расстояния от вершиныiдо вершинык. Заметим, что если некоторая дугаvVсодержится в кратчайшем пути из некоторой вершины i(например из вершиныh₁(v) ) в вершинуs, то для нее. Если нашлась дугаvV , для которой, то оценкиW_iне дают кратчайшие расстояния от вершинiдо вершиныs так как оценкуможно улучшить, положив. На этом свойстве основан алгоритм Флойда.

Алгоритм.

Первый этап.

0–шаг(задание начального приближения).

Положить для всех iE\{к} W_i=, для i=к W_к=0;

j–ый шаг. (j=1,2,3,...)

Среди всех дуг vVищем дугу (обычно в порядке нумерации), для которой , если такой дуги не существует, то переходим к выполнению второго этапа, в противном случае полагаем, для вершины запоминаем дугу выходаv, и переходим к выполнению следующего шага.

Второй этап.

Если W_н<, то выполняем второй этап алгоритма Беллмана–Калабы, в противном случае задача решения не имеет.

Пример. В качестве примера рассмотрим предыдущую задачу. Для нее таблица, которую уже внесено начальное приближение имеет вид:

На графе ищем дугу, для которой ,

вершина	1	2	3	4	5	6
(W,v)	(, –)	(, –)	(, –)	(, –)	(, –)	(, –)

Таковой является v₆, для нее h₁(v₆)=2, h₂(v₆)=6, поэтому полагаем W₂=4+W₆=4, заменяем значения в клетке 2 на (4, v₆), получим

вершина	1	2	3	4	5	6
(W,v)	(, –)	(4, v6)	(, –)	(, –)	(, –)	(, –)

Следующей будет дуга v₆, поэтому полагаемW₁=1+W₂=4, поэтому

вершина	1	2	3	4	5	6
(W,v)	(5, v3)	(4, v6)	(, –)	(, –)	(, –)	(, –)

И так далее, на последнем шаге получим таблицу

вершина	1	2	3	4	5	6
(W,v)	(4,v3)	(3,v4)	(2,v7)	(2,v8)	(1,v10	(0,–)

Восстанавливая по этой таблице путь путь, получим ранее полученное решение.

Алгоритм Дейкстры отыскания кратчайших расстояний на графе.

Алгоритм Дейкстры применяется для случая, когда c_v>0. В нем каждая вершина может быть:

a) непомеченной,

b) помеченной временной пометкой,

c) помеченной постоянной пометкой.

Вершина iнепомечена, если для нее не найдено ни одного пути из вершинын, помечена временной пометкой, если из вершиныннайден путь и величинаW_iесть верхняя оценка кратчайшего расстояния отндоi(и на последующих итерациях величинаW_iможет быть уточнена вплоть до кратчайшего расстояния отндоi). Помечена постоянной пометкой, еслиW_iиз верхней оценки стала кратчайшим расстоянием отндоi. Алгоритм первого этапа заканчивает работу, если вершинакстала помеченной постоянной пометкой, в этом случаеW_кстало равным кратчайшему расстоянию отндок.

Первый этап.

0–шаг.Для всехiE\{н} полагаемW_i=M , эти вершины считаем непомнеченными, дляi=н полагаемW_i=0, эту вершину считаем помеченной временной пометкой,

k–ый шаг. Ищем, где минимум берется переменнойi среди все временно помеченных вершин. Вершинуjпомечаем постоянной пометкой. Еслиj=к, то найдено кратчайшее расстояние до этой вершины, и переходим к восстановлению кратчайшего пути, выполняемого на втором этапе, в противном случае «просматриваем» вершинуj, т.е. для всехвыполняем:

a) определяемi=h₂(v),

b) полагаемW_i=min(W_i, c_v+W_j), помечаем эту вершину временной пометкой и переходим к выполнению ( K+1) шага.

Второй этап.(восстановление кратчайшего пути)

Так как движение идет от конца пути к началу, то применим обратный отсчет шагов, в нем начальный шаг N=|E|.

N–шаг.Полагаем ;

k–ый шаг(k=N–1,N–2,…). Средиищем, для которой

, полагаем. Если , то алгоритм заканчивает работу, в противном случае переходим к выполнению (k–1) –го шага.

Пусть kномер шага, на котором остановился алгоритм второго этапа, тогда решение задачи имеет вид.

Замечание.Для отыскания кратчайшего расстояния между двумя вершинами достаточно, чтобы только конечная вершина получила постоянную пометку. Если требуется найти кратчайшее расстояние от начальной вершины до всех остальных, то следует выполнять алгоритм до тех пор, пока все вершины не окажутся помечеными постоянной пометкой.

Пример. Рассмотрим вновь пример, который приведен на следущем рисунке:

0–й шаг.Все вершины непомечены, в них в квадратах около вершин записаны «», кроме вершины 1, около нее в квадрате записано «0». Далее будем считать, что если в прямоугольнике не «», то вершина непомечена, если это число не, вершина помечена временной пометкой, если квадрат затемнен, то пометка постоянная.

2–й шаг. Среди всех временно помеченных вершин выбираем вершину с наименьшей величиной пометки, это вершина 1, она становится постоянно помеченной, из нее по инцидентным дугам просматриваются вершины 2,4,3. Для них соответственно, , . Эти значения вносим в рисунок

2–й шаг. Повторяем процедуру, аналогичную шагу 2, но теперь для вершины 1.

Заметим, что величина пометки вершины 4 уменьшилась после просмотра вершины 1.

3–й шаг. Просматриваем вершину 4, так как у нее наименьшая пометка, будем иметь

4–й шаг. Просматриваем вершину 3 (можно и 5, ), при ее просмотре в других вершинах ничего не изменяется.

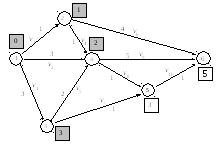
5–й шаг. Просматриваем вершину 5, получим

6–й шаг. Постоянно помеченной вершиной становится вершина 6. До нее найдено кратчайшее расстояние. Оно равно 4.

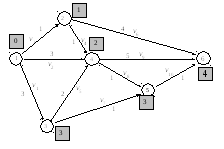
Работу второго этапа также продемонстрируем на рисунке. Среди дуг, входящих в вершину 6, выделим дугу, для которой выполняется равненство . Таковой является дугаv₁₀. Для нее 3+1=4, вершина – начало этой дуги равно 5.

Теперь эту же процедуру проведем для вершины 5, и так далее. Получим путь, изображенный на рисунке