Решения дополнительных задач по курсу "Квантовая теория"

1. Доказать соотношение:

Решение.

Введём оператор и разложим его в ряд Тейлора в точке:

При этом

Аналогично находим производные более высокого порядка:

и т.д.

Тогда

2. В состоянии частицы с волновой функцией 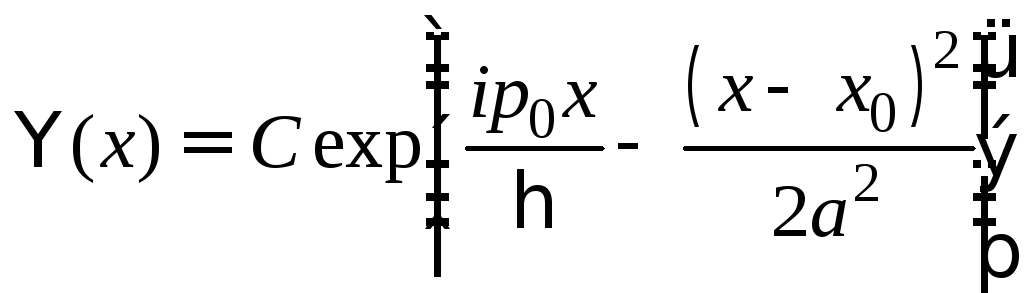, где,,a-вещественные параметры, найти распределение вероятностей различных значений координаты. Определить средние значения координаты и импульсачастицы, а также средние значения их квадратов,. Показать, что такая в.ф. минимизирует соотношение неопределённостей: . Состояния, минимизирующие соотношение неопределённостей, называются когерентными.

Решение.

Нормировка волновой функции на единицу даёт . Действительно, имеем:

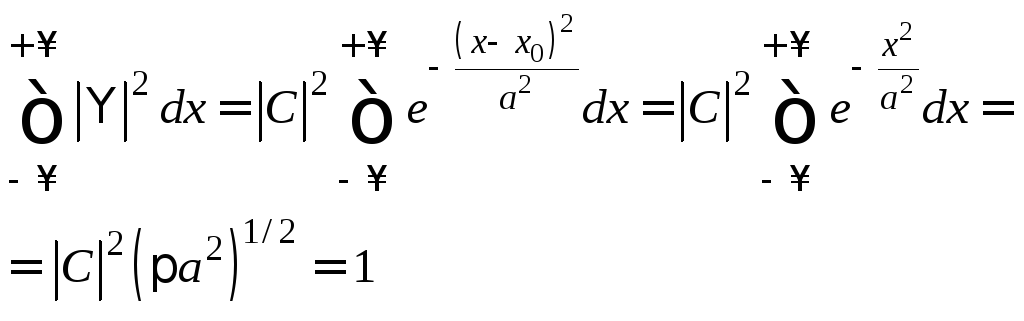(1)

Гауссов интеграл 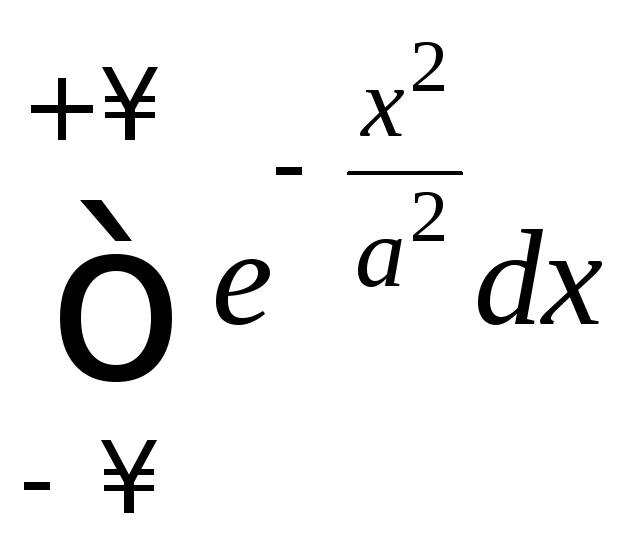в (1) может быть вычислен путём сведения к кратному интегралу следующим образом:

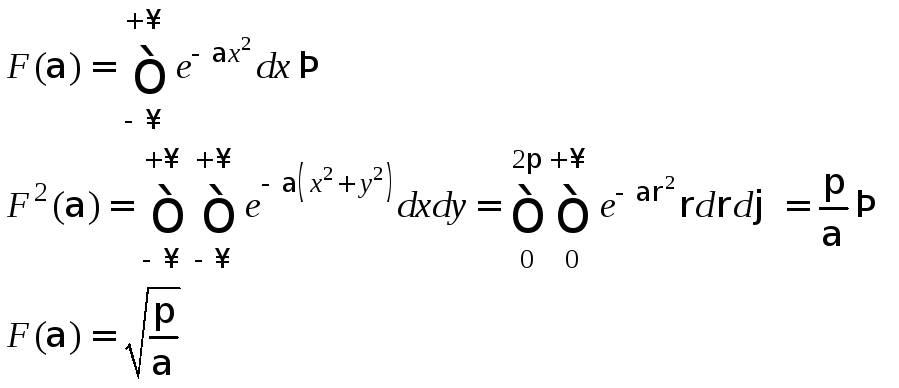(2)

По формуле (1) из параграфа 12 получаем, используя (2):

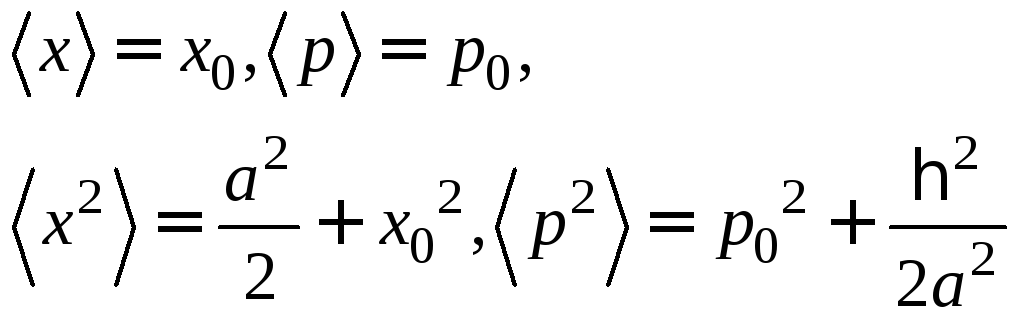(3)

Проверка того, что тривиальна.

3. Найти собственные функции и собственные значения физической величины, представляющей линейную комбинацию одноименных компонент импульса и координаты частицы:. Убедиться в ортогональности полученных функций и нормировать их соответствующим образом.

Решение.

Уравнение для собственных функций и собственных значений оператора имеет вид:

(1)

Решением (1) служат функции (они же собственные функции искомого оператора)

(2)

Из (2) конечности в.ф. следует, что с.з. f– произвольные действительные величины, иначе в.ф. (2) будет неограниченно возрастать на больших расстояниях. Т.о. получаем, что спектр искомого оператора непрерывен и состоит из всех точек действительной оси. Условие нормировкиприводит к значению(см. формулу (2) из предыдущей задачи).

4.Найти уровни энергии и нормированные волновые функции состояний дискретного спектра частицы в-потенциале,. Найти средние значения кинетической и потенциальной энергии в этих состояниях. Вычислить произведение неопределенностей координаты и импульса. Каков вид волновой функции в импульсном представлении?

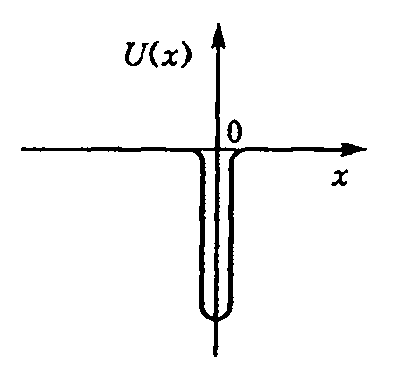
Решение.

Решение уравнения. Шредингера. с () имеет вид

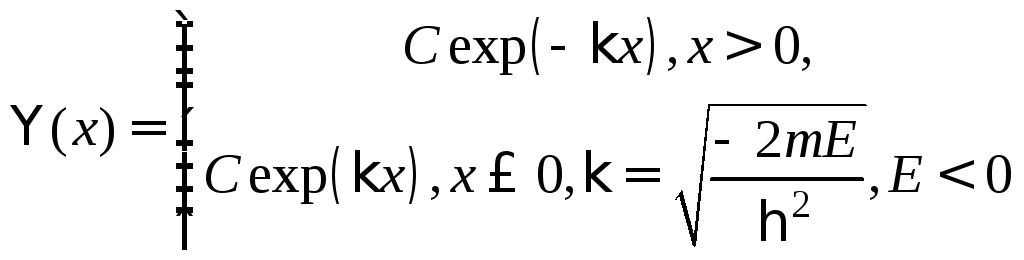(1)

В (1) E– энергия частицы (меньше нуля, так как ищем состояния дискретного спектра),m– масса частицы. Действительно, интегрируя уравнение Шредингера с таким потенциалом в окрестностиx=0 и используя свойства дельта функции

,

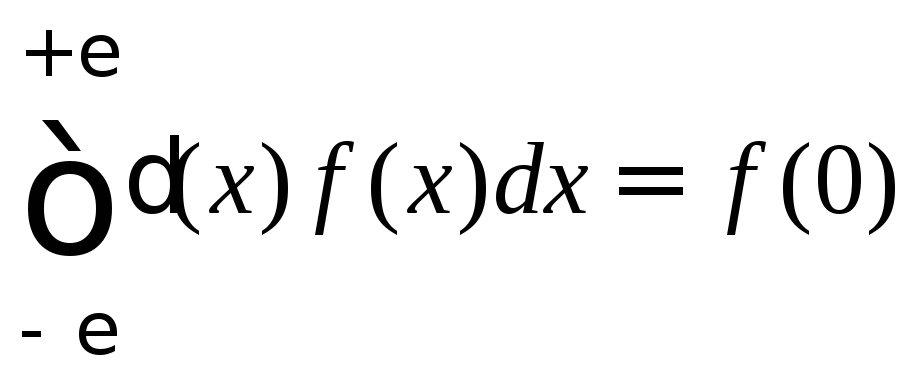получим граничные условия на в.ф. в точке x=0:

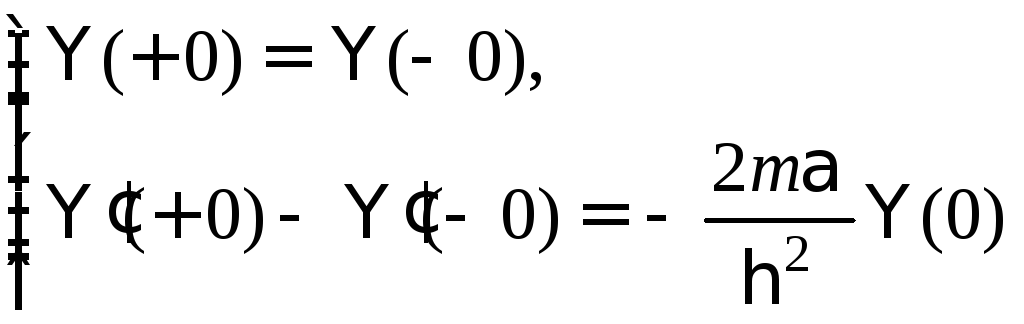(2)

Слева и справа от нуля потенциал U(x) равен нулю (дельта функция “сосредоточена” в одной точке). Учитывая, что в.ф дискретного спектра должна убывать на бесконечности, получаем и из (2) вид в.ф. (1). При этом получаем всего одно состояние дискретного спектра, энергию которого получаем из граничного условия (2):

(3)

Волновая функция, нормированная на единицу и соответствующая (3):

(3)

Элементарные выкладки дают для искомых средних:

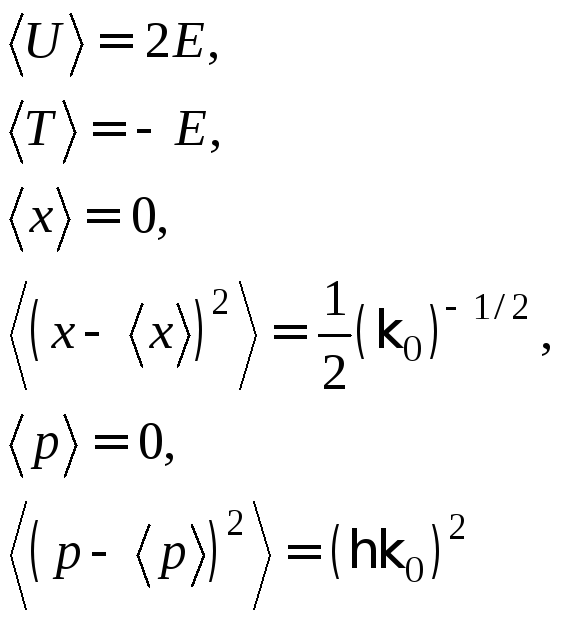
В.ф. (3) в импульсном представлении:

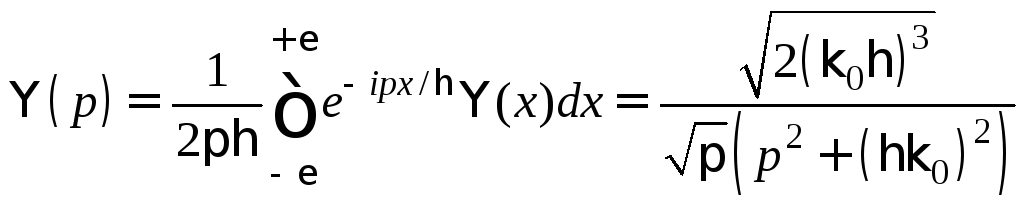
5. Найти связанные состояния и соответствующие им собственные значения в случае прямоугольной потенциальной ямы

Решение.

Потенциал инвариантен по отношению к инверсии U(х) =U(-x), так что решения уравнения Шредингера обязаны быть либо четными, либо нечетными. В нашем случае чётные и нечётные решения выглядят так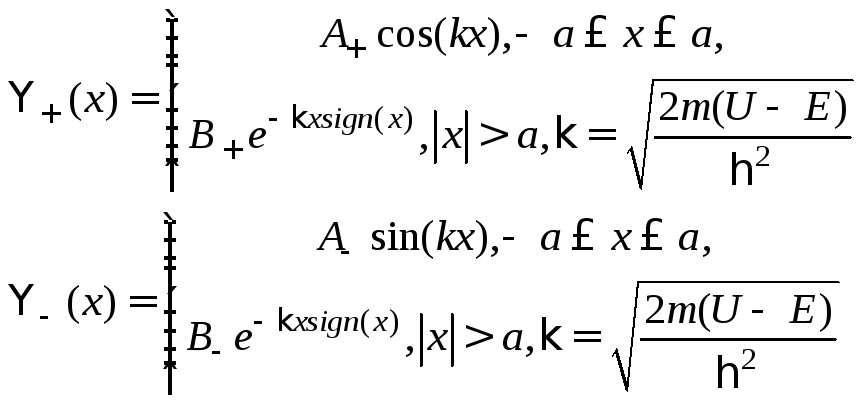¹:

(1)

Условие непрерывности в.ф. и их производных на границе даёт:

- для чётных состояний, (2)

- для нечётных состояний. (3)

Последние два уравнения можно описать свести к одному:

(4)

В (4) чётные nсоответствуют дискретным состояниям в яме, описываемым уравнением (2) (нечётные состояния), а нечётныеn– состояниям, описываемым уравнением (3).

6. Найти значения энергий, при которых частицы не отражаются от потенциального барьера вида.

Решение.

Пользуясь свойством дельта-функции, пишем граничные условия для в.ф. в точках x=0 иx=a. При этом (отражения от барьера нет):

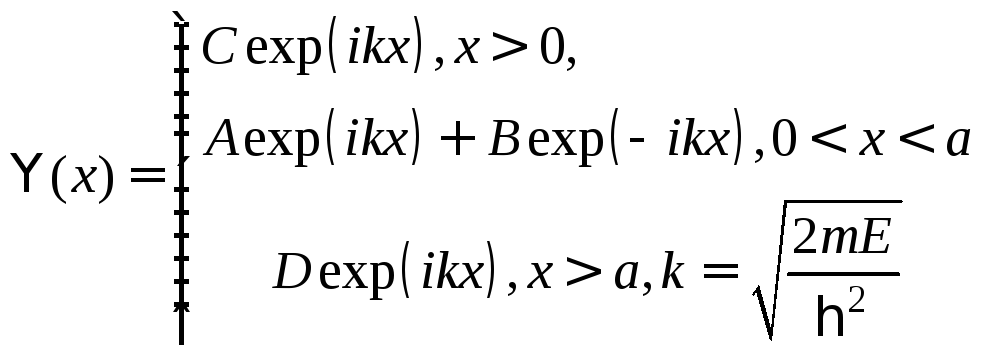(1),

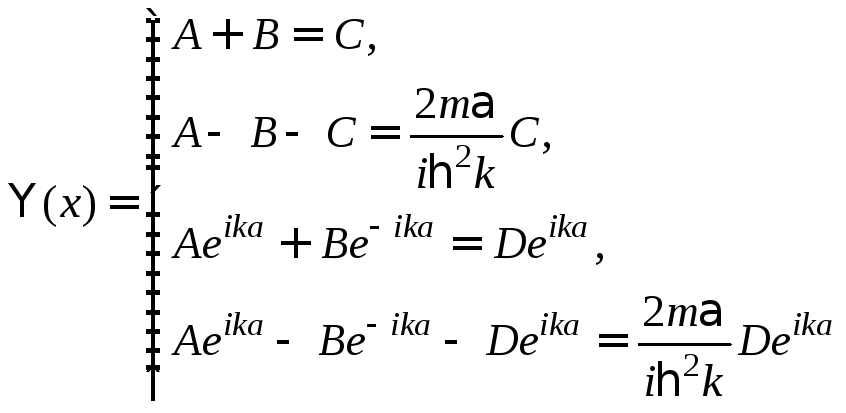(2)

Условием разрешимости (2) является равенство нулю детерминанта. Это условие и определяет искомые значения энергии, при которых не происходит отражения от барьера. Искомое условие сводится к

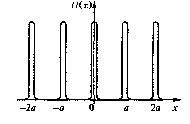
7.Для частицы в периодическом потенциале вида(идеальный бесконечный «кристалл», см. рис. 1) найти систему независимых решений уравнения Шрёдингера для произвольного значенияE. Определить энергетический спектр частицы.

Решение.

Общее решение уравнения Шредингера при na<x<(n+1)aимеет вид:

(1)

Где E– энергия,m– масса. Рассматривая независимые решения, удовлетворяющие условию²

(2),

получаем:

(3)

Условия сшивки в.ф. на краях ячеек приводят к следующему:

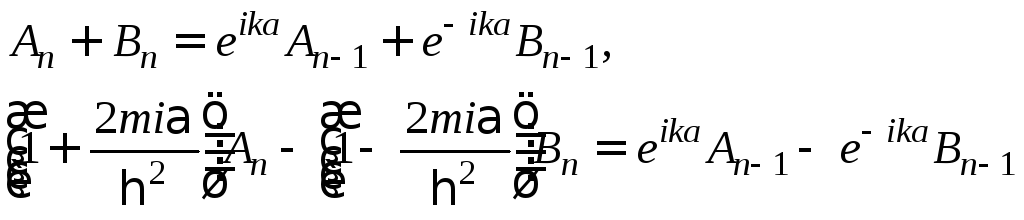(4)

Система (4) –система линейных однородных уравнений, условие разрешимости которой с учётом (3) даёт:

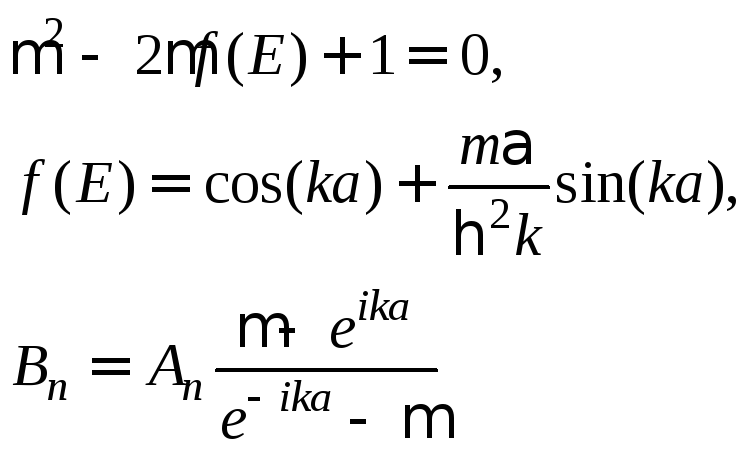
Отсюда

.(5)

При любом фиксированном E(5) определяет два значения, соответствующие двум независимым решениям уравнения Шредингера, при этом. Если, то обоим значениямсоответствуют решения, возрастающие на бесконечности, таким образом, соответствующие решения нефизичны. Истинным состояниям частицы в периодическом потенциале соответствуют значения, или

(6)

Таким образом, допустимые значения Е образуют зоны. Если положить, где,— так называемый квазиимпульс, то уравнение (5) для определения зависимостиE_n(q) принимает вид (n+1 — номер зоны, см. рис. 2 для):

(7)

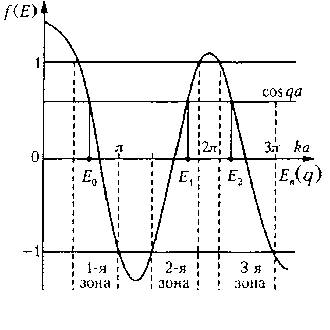
Рис. 2.

8.Найти сдвиг в слабом электрическом поле и поляризуемость основного уровня

заряженной частицы в одномерном -потенциале.

Решение.

Для основного уровня частицы в -потенциале имеем (см. зад. 1)³:

,(1)

Для вычисления его сдвига под действием возмущения во втором порядке теории возмущений (очевидно, что поправка первого порядка, равная диагональному элементу возмущения в состоянии с чётной в.ф (1) равна нулю) в качестве невозмущенных с. ф. непрерывного спектра удобно выбрать функции, отвечающие определенной четностиI= ±1. Так как для четных с. ф. гамильтониана, искажаемых- потенциалом, матричный элемент возмущения равен нулю (и поэтому их явный вид несуществен), а нечетные в. ф. не искажаются им и поэтому совпадают с в. ф.свободной частицы, то получаем следующее⁴:

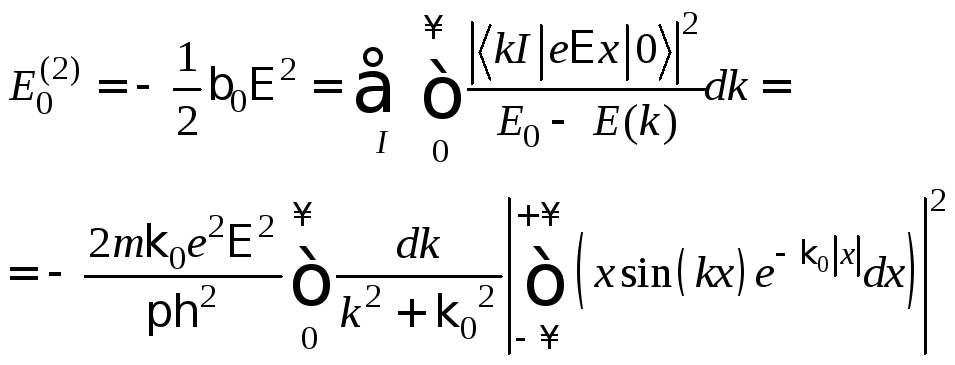(2)

В итоге, поправка второго порядка к энергии и поляризуемость:

9.1) Найти собственные функции и собственные значения операторов рождения и уничтожения. В рассматриваемых состояниях найти распределение по числу частиц. Обсудить случаи бозонных и фермионных операторов. 2) Показать, что применительно к линейному осциллятору собственные функции оператораописывают когерентные состояния.

Решение.

1. Операторы уничтожения и рождения 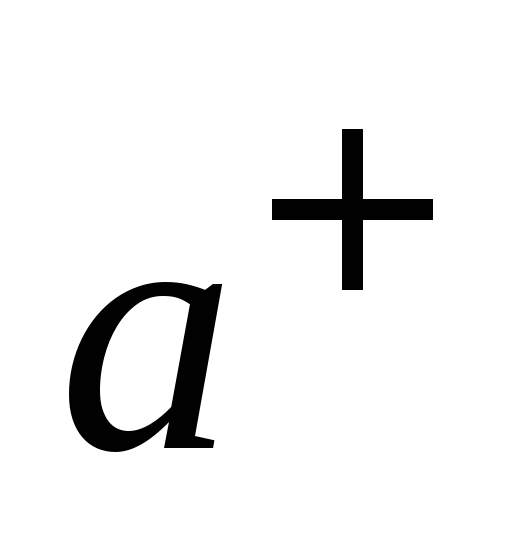действуют в пространстве функций - векторов состояний:

,(1)

Где символ соответствует n-частичному состоянию. При этом, по определению, оператор уничтожения уменьшает число частиц на единицу, а оператор рождения- увеличивает на единицу:

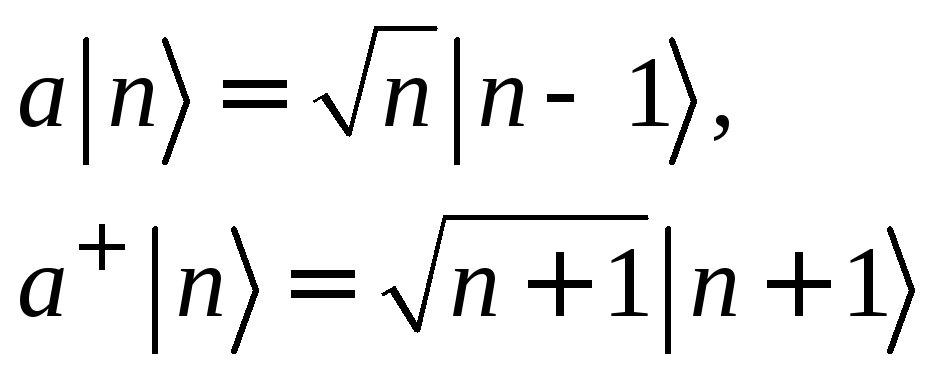(2)

В случае бозонов операторы рождения и уничтожения подчиняются следующим коммутационным соотношениям:

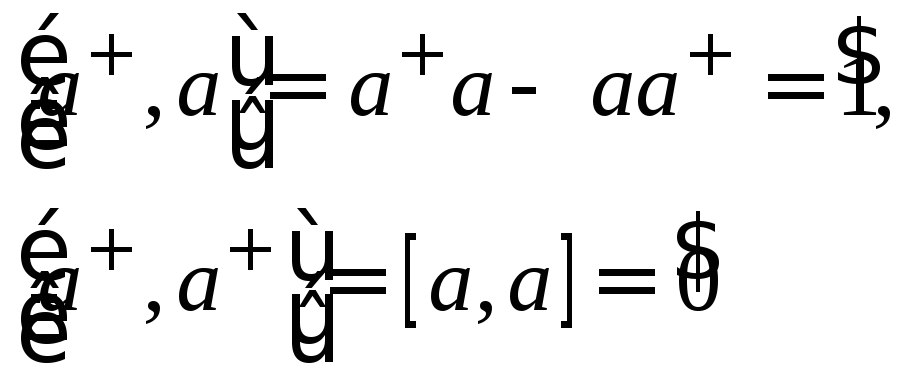(3)

Для ферми частиц:

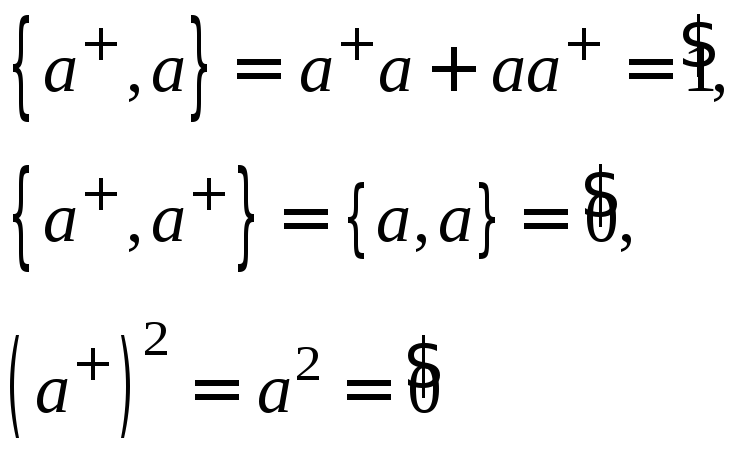(4)

Собственные функции и собственные значениябозонного оператораaопределяются из уравнения. Тогда из (2) получаем:

Отсюда, с учётом независимости состояний получаем:

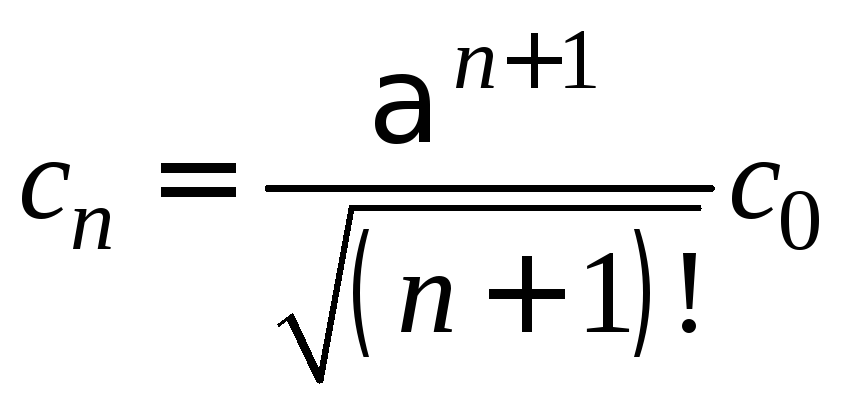
Как видно, собственным значением бозонного оператора а является любое комплексное число (операторa— неэрмитов), а соответствующая с. ф.может быть нормирована

на единицу. Условие даст:

При этом распределение по числу частиц в состоянии определяется выражением:

,

То есть представляет собой распределение Пуассона. Уравнение на с. ф и с з. бозонного оператора a⁺не имеет ни одного решения. У фермионных же операторовa,a⁺имеется по одной с ф.:— с фa,- с.фa⁺, а соответствующие им с.з. в обоих случаях равны 0.

2. Нетрудно показать, используя правила коммутации, что оператор 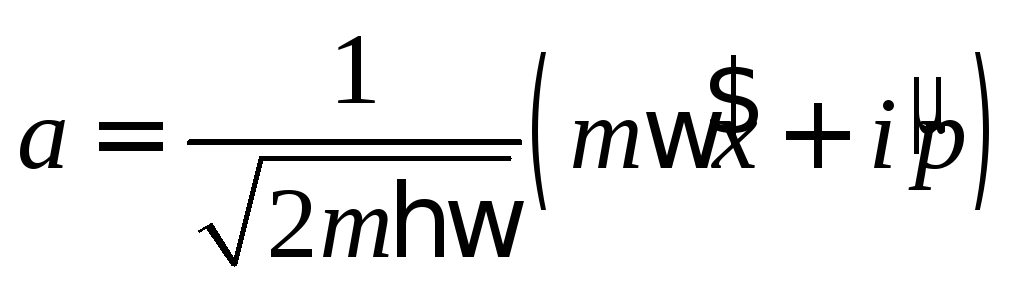и эрмитово сопряжённый к нему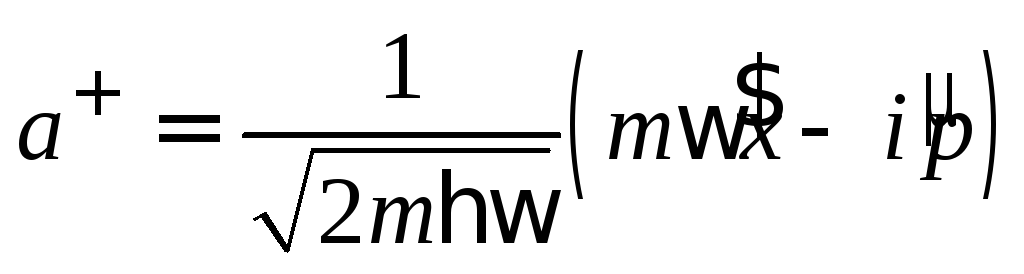являются операторами уничтожения и рождения в смысле (3). Искомая с.ф. оператораa:

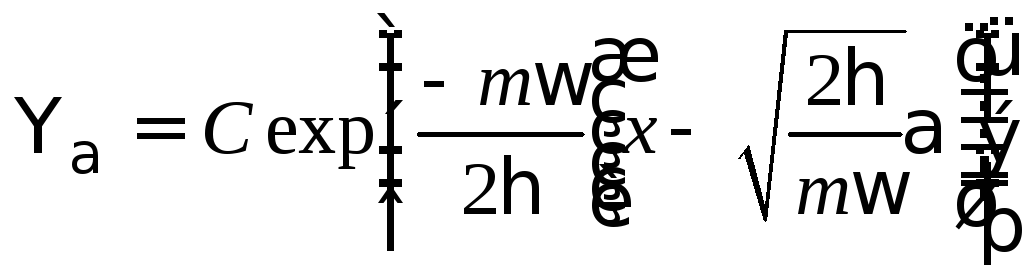(5)

Она соответствует в.ф. из задачи 1 к параграфу 11, для которой минимизируется соотношение неопределённостей. Т.о., в.ф. (5) соответствует когерентному состоянию.

10.Состояние свободной частицы при t = 0 описывается волновой функцией

Найти изменение во времени и следующие средние: .

Решение.

Разложим в. ф. по с.ф. оператора импульса, являющимися также с.ф. гамильтониана свободной частицы:

(1)

Отсюда

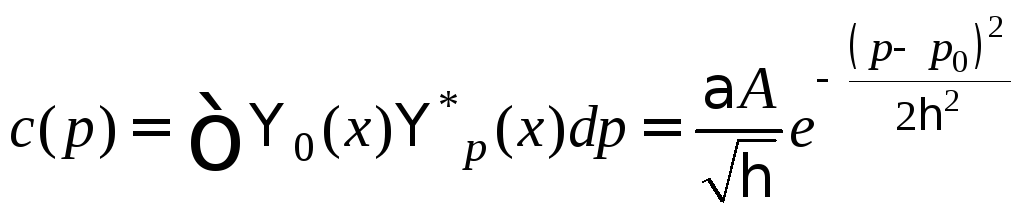(2)

Далее,

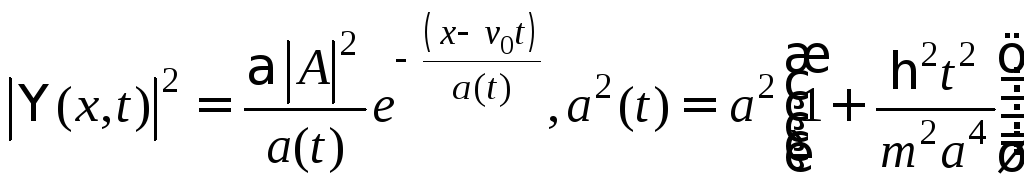
Выбрав для нормировки в.ф. на единицу, получим:

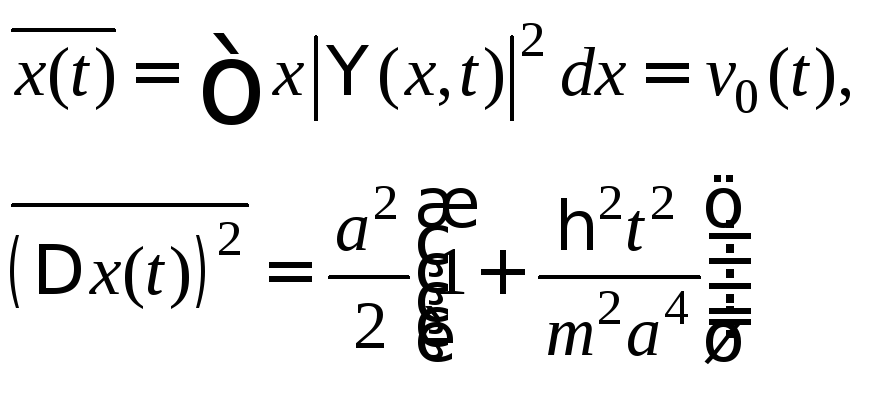
Так как является в.ф. в импульсном представлении, то:

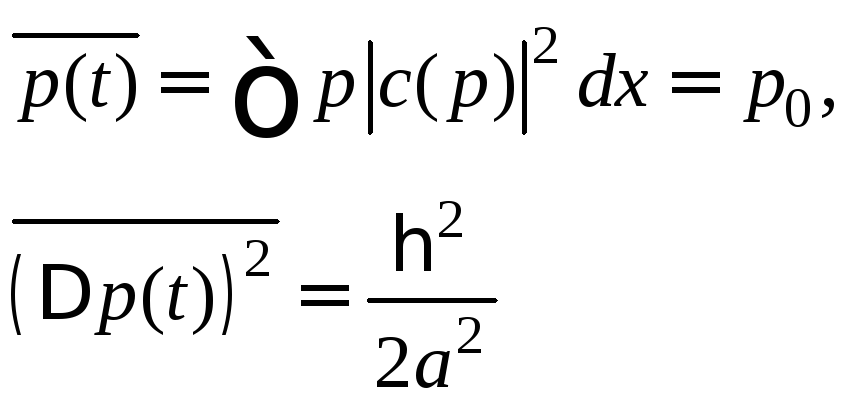
Видим, что импульсные средние не зависят от времени, что является отражением того факта, что для свободной частицы импульс сохраняется.

11. Найти унитарный оператор, соответствующий преобразованию Галилея, т.е. переходу в новую инерциальную системы отсчета. Убедиться в инвариантности уравнения Шрёдингера относительно этого преобразования. Как при этом преобразуется волновая функция частицы в координатном и импульсном представлениях?

Решение.

Пусть система К1движется со скоростьюVвдоль оси х относительно системыK, так что х = х' + Vt, t = t'. Потенциальные энергии частицы в этих системах связаны соотношением

(1)

Унитарный оператор , соответствующий преобразованию Галилея, находится из того

условия, что если волновая функцияудовлетворяет уравнению Шредингера в системеK:

, (*)

то функция должна являться решением у. Ш. в системеК'(и наоборот):

(2)

Так как обе функции описывают одно и то же физическое состояние частицы (но по отношению к различным системам координат), то должно быть выполнено условие:

, (3)

выражающее независимость от выбора системы координат плотности вероятности нахождения частицы в данной точке пространства. Из (3) следует, что искомый оператор имеет вид

,

где S(x,t) — вещественная функция.Подставив в уравнение (2) функцию

и перейдя в нем к переменным х, t, получим:

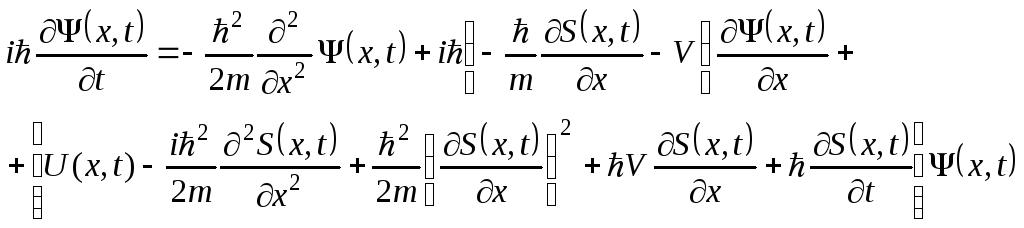(4)

Потребовав, чтобы это уравнение было тождественно (*), приходим к системе уравнений:

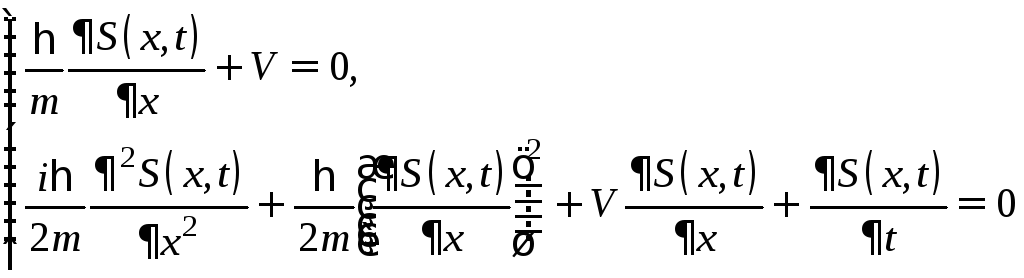(5)

Из первого из них следует, что ,aвторое позволяет найтии получить:

(6)

Несущественную постоянную в (6) можно опустить. Теперь найдем закон преобразования волновой функции частицы в импульсном представлении. Умножив на(с. ф. оператора импульса) и проинтегрировав по х' с учетом (6), получаем:

,

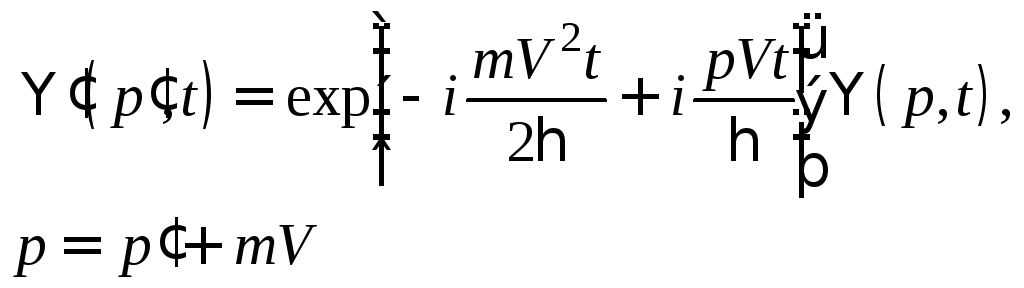Откуда

-

соотношение, связывающее плотности вероятностей в разных инерциальных системах отсчёта.

12.Найти унитарный оператор, соответствующий калибровочному преобразованию потенциалов электромагнитного поля. Убедиться в инвариантности уравнения Шредингера относительно этого преобразования.

Решение.

Пусть в. ф. является решением уравнения Шредингера:

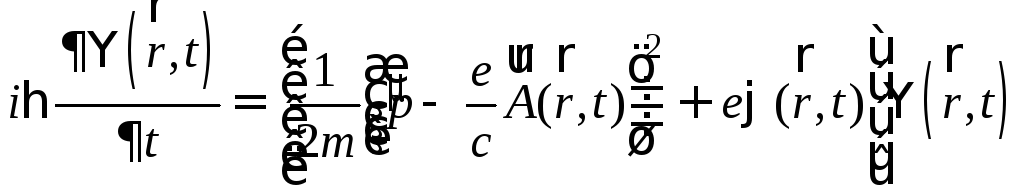, (1)

где ,- потенциалы электромагнитного поля. Инвариантность уравнения Шредингера относительно калибровочного преобразования потенциалов означает, что, если перейти к новым потенциалам

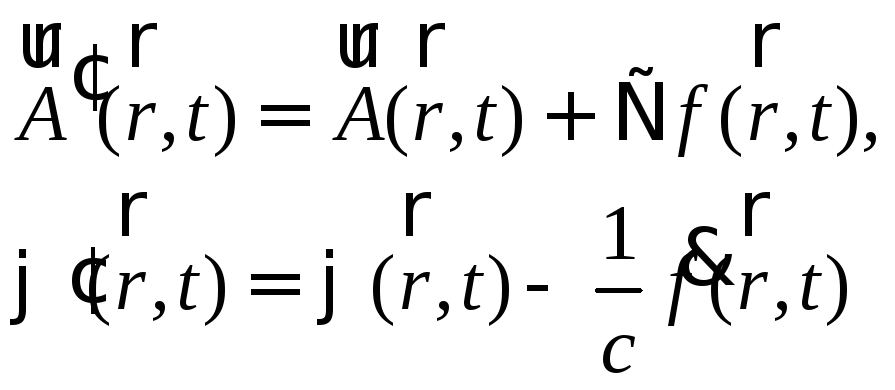(2)

то должен существовать такой унитарный оператор , что волновая функция, описывающая то же самое физическое состояние частицы, что и исходная в. ф.(но с другим выбором потенциалов), и поэтому удовлетворяющая соотношению

, (3)

является решением уравнения Шредингера

(4)

Ввиду (3), искомый оператор должен иметь вид:

(5),

где - вещественная функция. Подставив в. ф. вида

в (4), и потребовав, чтобы получающееся уравнение совпадало с уравнением (1), приходим к соотношениям:

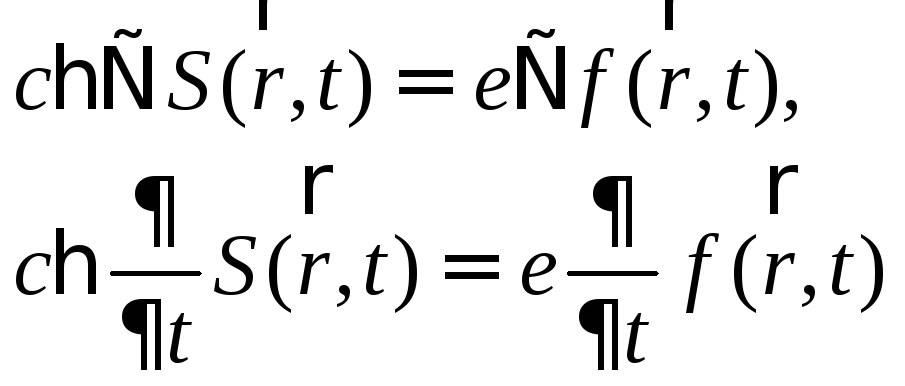(6)

Отсюда находим , что и решает задачу (несущественную постояннуюздесь можно опустить).

13.Исследовать энергетический спектр поперечного движения заряженной бесспиновой частицы в однородном магнитном поле, введя соответствующим образом выбранные операторы рождения и уничтожения. Воспользоваться выражениемдля векторного потенциала.

Решение.

Гамильтониан поперечного движении частицы в магнитном поле имеет вид (см., например, Ландау, Лифшиц, “Квантовая механика”):

(1)

Введём обычным образом операторы уничтожения (и рождения) “квантов колебаний” вдоль осей х и у (см. задачу выше):

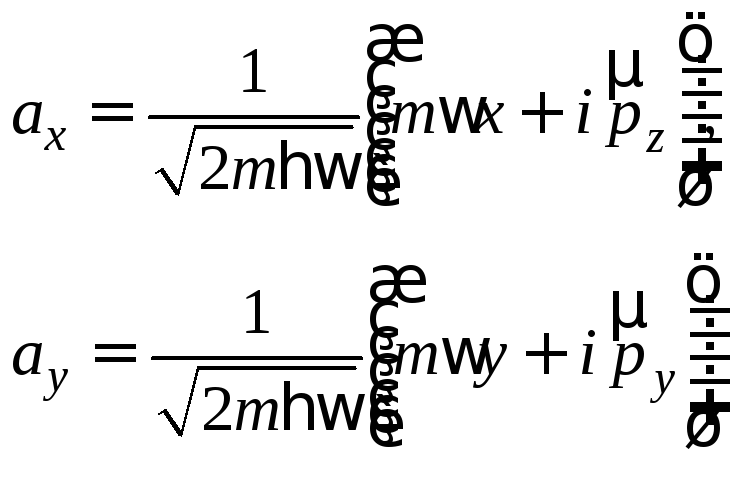(2)

Тогда (1) можно записать так:

(3)

Для удобства введём следующие операторы:

, (4)

Которые удовлетворяют тем же коммутационным соотношениям, что и :

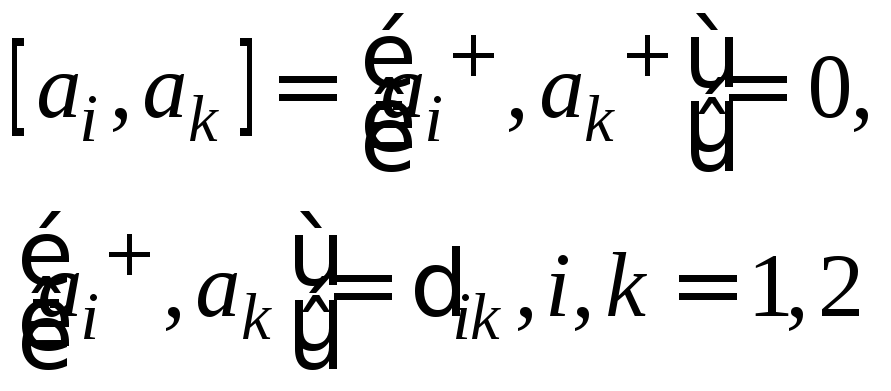
Тогда гамильтониан (3) запишется в виде:

(5)

Так как эти операторы выражаются только через операторы чисел квантов , то собственные векторы последних являются также собственными векторами гамильтониана Н и оператора l_z. Отсюда сразу следует выражение для спектра уровней Ландау:

(6)

В силу того, что энергия уровней Ландау (6) не зависит от , то они бесконечно вырождены.