
- •Московский государственный институт электронной техники (Технический Университет)
- •§2. Классическое и квантовое описание системы
- •§3. Принцип неопределенности
- •§4. Полный набор динамических переменных
- •§5. Постулаты квантовой механики
- •§6. Роль классической механики в квантовой механике
- •§7. Волновая функция и ее свойства
- •§8. Принцип суперпозиции состояний
- •§9. Понятие о теории представлений
- •§10. Операторы в квантовой механике
- •Транспонированный оператор
- •§11. Собственные функции и собственные значения эрмитовых операторов. Случай дискретного и непрерывного спектра
- •§12. Среднее значение измеряемой величины
- •§13. Вероятность результатов измерения
- •§14. Коммутативность операторов и одновременная измеримость физических величин
- •§15. Операторы координаты , импульса, момента импульса, энергии
- •§16. Решение задачи на собственные функции и собственные значения для оператора
- •§17. Решение задачи на собственные функции и собственные значения для оператора .
- •§ 18. Вычисление коммутаторов, содержащих операторы
- •§ 19 Волновое уравнение
- •§ 20 Производная оператора по времени
- •§ 21 Интегралы движения в кв. Механике
- •§22. Флуктуации физических величин
- •§ 23. Неравенство Гайзенберга
- •§ 24 Оператор Гамильтона различных систем
- •§ 25. Стационарное состояние различных систем
- •§ 26. Решение волнового уравнения в случае свободной материальной точки
- •§ 27. Решение волнового уравнения в случае бесконечно глубокой потенциальной ямы
- •§ 28. Метод (представление) Шредингера. Оператор эволюции и его свойства
- •§ 29. Метод (представление) Гайзенберга. Уравнение движения для оператора
- •§ 30. Уравнение эволюции среднего значения физической величины. Соотношение неопределенности: время – энергия
- •§ 31. Матричное представление операторов
- •§ 32. Энергетическое представление
- •§ 33. Уравнение Шредингера в матричной форме
- •§ 34*. Матричная формулировка задачи о линейном гармоническом осцилляторе
- •§ 35*. Расчет матричных элементов операторов
- •§ 36. Собственный механический момент (спин)
- •§ 37. Операторы ии их свойства
- •§ 38. Спиновая переменная волновой функции
- •§ 39. Матрицы Паули и их свойства
- •§ 40. Принцип тождественности
- •§ 41. Оператор перестановки и его свойства
- •§ 42. Симметричное и антисимметричное состояния
- •Решения задач по курсу "Квантовая теория"
- •Решения дополнительных задач по курсу "Квантовая теория"
- •Экзаменационные вопросы по курсу "Квантовая теория".
- •Экзаменационные задачи по курсу "Квантовая теория".
- •Дополнительные задачи по курсу “Квантовая теория”.
§ 42. Симметричное и антисимметричное состояния
Чтобы построить конкретные функции будем рассматривать ансамбль независимых частиц, т. е. они между собой не взаимодействуют, но могут находиться во внешнем поле.
Для i-ой частицы во внешнем поле:
![]()
Так как частицы одинаковые, то их массы
одинаковые, т. е.
![]() .
.
Полный оператор
![]() (51.1)
(51.1)
Для
![]() одинаковые аналитические выражения
(закон один), но здесь разные координаты.
одинаковые аналитические выражения
(закон один), но здесь разные координаты.
Когда оператор
![]() представим в виде (51.1), то можно провести
разделение переменных
представим в виде (51.1), то можно провести
разделение переменных
![]() .
.
Тогда уравнение
![]()
разбивается на Nодинаковых уравнений:
![]()
![]() - волновая одночастичная функция.
- волновая одночастичная функция.
![]() - это набор квантовых чисел, характеризующих
одночастичное состояние.
- это набор квантовых чисел, характеризующих
одночастичное состояние.
Тогда
![]() (51.2)
(51.2)
![]() - это все квантовые числа, относящиеся
к рассматриваемому ансамблю.
- это все квантовые числа, относящиеся
к рассматриваемому ансамблю.
![]()
Причем
![]() ,
,
где
![]() .
.
Учтем действие оператора перестановки:
Рассмотрим симметричные состояния.
![]()
Однако из (51.2) при перестановке мы получаем другую функцию. Но в (51.2) функция еще не симметричная. Симметризуем ее:
![]()
Здесь сумма по всем нетождественным перестановкам частиц.
![]() - постоянная нормировки
- постоянная нормировки
![]() ,
,
где
![]() .
.
Рассмотрим случай двух частиц
![]()
Для данного случая
![]() .
.
Так как бозоны могут находиться в неограниченном количестве в одном и том же состоянии, то здесь когда говорим о нетождественных состояниях, то имеем в виду, что эта перестановка приводит к новому состоянию.
Если перестановка происходит в одном
и том же состоянии, то она тождественная
и выбрасывается из рассмотрения. Для
бозонов из N!перестановок![]() тождественные перестановки. Тогда надо
рассматривать
тождественные перестановки. Тогда надо
рассматривать![]() перестановок, гдеNвсего бозонов, а в 1-ом состоянии находитсяN1частиц,
во 2-омN2частиц и тд.
перестановок, гдеNвсего бозонов, а в 1-ом состоянии находитсяN1частиц,
во 2-омN2частиц и тд.
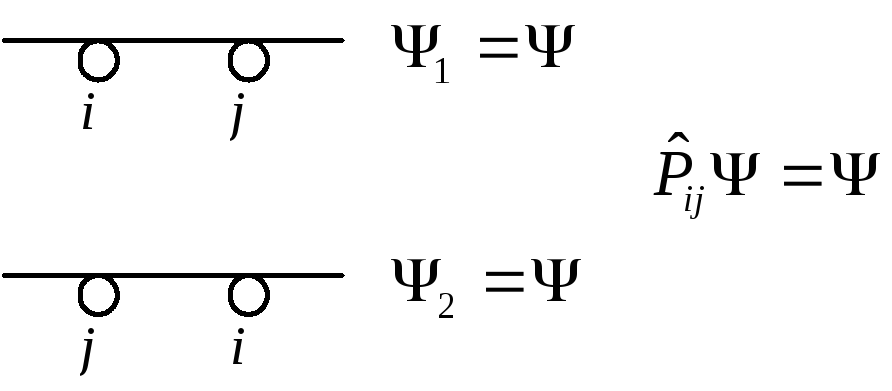
Симметричные состояния допускают произвольное число частиц в одночастичном состоянии.
Тогда нормировочный множитель
![]()
2. Рассмотрим антисимметричные состояния
Здесь
![]() (51.3)
(51.3)
![]()
Чтобы учесть знак вводят понятие парной (соседней, элементарной) перестановки.
Пусть надо переставить в ряде
![]() цифры 1 и 4. Учтем элементарные
перестановки:
2134, 2314, и т. д.
цифры 1 и 4. Учтем элементарные
перестановки:
2134, 2314, и т. д.
Здесь 5 элементарных перестановок.
![]() .
.
Тогда в сумму (51.3) надо поставить
![]() .
.
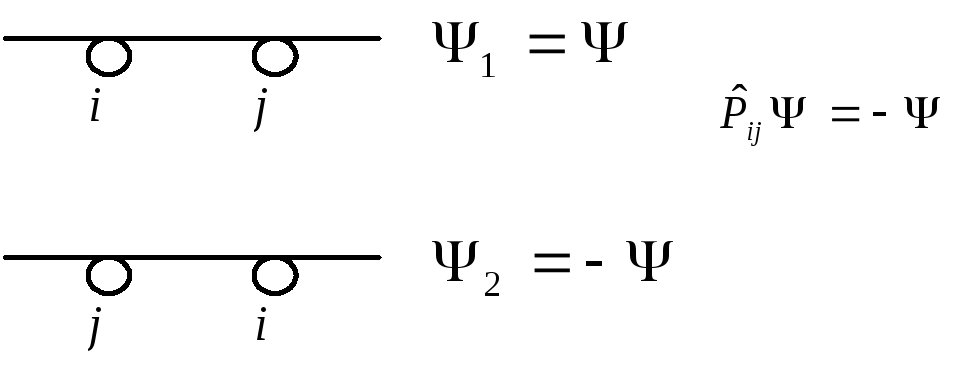
Если iиjв одном состоянии, то![]() ,
,![]() =>
=>
![]() .
.
Антисимметричные состояния запрещают нахождение более одной частицы в одночастичном состоянии.
В сумме (51.3) оператор
![]() это оператор не элементарной перестановки,
а какой-то конкретной перестановки.
это оператор не элементарной перестановки,
а какой-то конкретной перестановки.
Итак получаем из (51.3) выражение
![]()
Рассмотрим пару частиц, тогда
![]()
Эта функция обладает свойством антисимметричности. Подействуем на нее оператором перестановки:
![]() ,
,
т. е.
![]() - собственная функция оператора
перестановки.
- собственная функция оператора
перестановки.
Здесь
![]() т. к. у фермионов в каждом одночастичном
состоянии число частиц не превышает 1,
т. е. 0 или 1.
т. к. у фермионов в каждом одночастичном
состоянии число частиц не превышает 1,
т. е. 0 или 1.
В наиболее общем виде
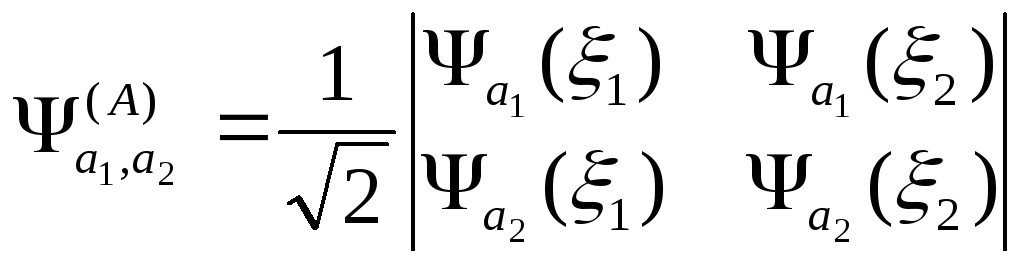 .
.
Обобщим
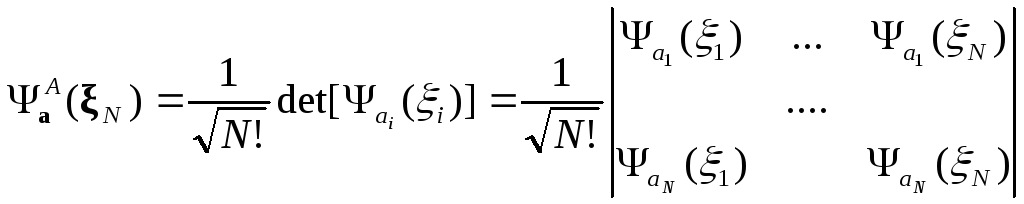
Из этого вида вытекает принцип Паули: не более одного фермиона может находиться в одном квантовом состоянии.
Допустим две частицы в одном квантовом
состоянии, тогда у них совпадают квантовые
числа, т. е.
![]() .
Тогда для детерминанта имеем 2 одинаковые
строки, он равен нулю. Состояние не
реализуется.
.
Тогда для детерминанта имеем 2 одинаковые
строки, он равен нулю. Состояние не
реализуется.
Решения задач по курсу "Квантовая теория"
Задача
1.Рассмотреть следующие операторы![]()
а)
инверсии
![]() ;
;
б)
трансляции
![]() ;
;
в)
изменения масштаба
![]() ;
;
г)
комплексного сопряжения
![]() .
.
Решение.
Представим![]() в форме
в форме
![]() ,
где
,
где![]() и
и![]() . (1.1)
. (1.1)
Учтем,
что соотношения а-г (см. условие задачи)
справедливы для каждой из функций
![]() ,
входящих в суперпозицию (1.1). Тогда имеем:
,
входящих в суперпозицию (1.1). Тогда имеем:
а)
![]()
![]() ;
;
б)
![]()
![]() ;
;
в)
![]()
![]() ;
;
г)
![]()
![]()
Таким образом, лишь последний из рассмотренных операторов не удовлетворяет свойству линейности.
Задача 2.Используя свойства
1.
![]() ; (2.1)
; (2.1)
2.
![]() ; (2.2)
; (2.2)
3.
![]() (2.3)
(2.3)
скалярного произведения
![]() ,
,![]() . (2.4)
. (2.4)
Доказать неравенство Коши-Шварца-Буняковского
![]() . (2.5)
. (2.5)
Решение.Запишем норму функции![]() вида
вида
![]() ,
где
,
где![]() -вещественное
число
-вещественное
число![]() .
.
Тогда
из
![]() с учетом (2.1)-(2.3) найдем
с учетом (2.1)-(2.3) найдем
![]()
![]() .
.
Ввиду
произвольности
![]() положительность нормы
положительность нормы![]() достигается при условии неположительности
дискриминанта
достигается при условии неположительности
дискриминанта
![]() ,
,
поставленного
в соответствие неравенству
![]() .
Легко видеть, что из
.
Легко видеть, что из![]() автоматически следует неравенство
(2.5). Знак равенства в формуле (2.5) имеет
место в том и только в том случае, когда
функция
автоматически следует неравенство
(2.5). Знак равенства в формуле (2.5) имеет
место в том и только в том случае, когда
функция![]() и
и![]() пропорциональны друг другу, т.е.
пропорциональны друг другу, т.е.
![]() ,
,![]() .
.
Задача
3.Найти оператор![]() ,
если
,
если
а)
![]() ,
,![]() ;
;![]() ,
,![]() ;
;
б)
![]() ,
,![]() ;
;![]() ,
,![]() .
.
Решение.Подставляя явный вид![]() в правую часть
в правую часть![]() и проводя интегрирование по частям,
получим
и проводя интегрирование по частям,
получим
а)
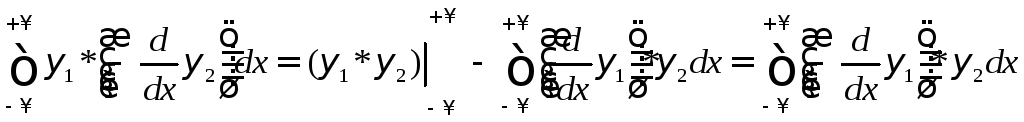 ,
,
![]()
б)
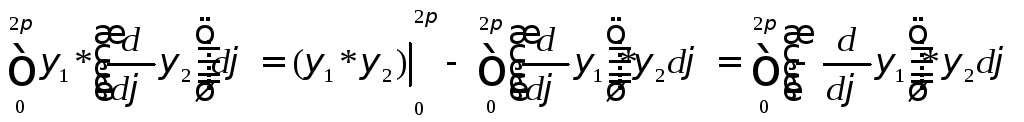 ,
,
![]() .
.
Здесь
использовано обращение функций
![]() и
и![]() в нуль на бесконечности в случае (а) и
условие периодичности функции
в нуль на бесконечности в случае (а) и
условие периодичности функции![]() и
и![]() в случае (б). В обоих случаях оператор
в случае (б). В обоих случаях оператор![]() не совпадает с оператором
не совпадает с оператором![]() .
.
Задача
4.Показать, что произвольный линейный
оператор![]() может быть представлен в виде
может быть представлен в виде
![]() ;
;![]() ,
,![]() .
.
Решение.Легко видеть, что справедливо разложение![]() на сумму
на сумму
![]()
двух операторов, первый из которых является эрмитовым:
![]() ,
,![]() ,
,
а второй – антиэрмитовым:
![]() .
.
С их помощью будем иметь
![]() ;
;![]() ,
,![]() ;
;
![]() ,
,![]() .
.
Всякая линейная комбинация эрмитовых операторов с вещественными коэффициентами есть Эрмитов оператор. Произведение двух эрмитовых операторов не обязательно эрмитово.
Задача
5.Найти![]() ,
если
,
если![]() -
произведение эрмитовых операторов
-
произведение эрмитовых операторов![]() и
и![]()
Решение.
Из определения![]() имеем
имеем
![]() ;
;
![]() ,
,![]() /
/
Отсюда
с учетом эрмитовости
![]() и
и![]() найдем
найдем
![]() . (5.1)
. (5.1)
Легко
видеть, что в общем случае
![]() .
.
Задача
6. Показать, что при условии эрмитовости![]() и
и![]() операторы
операторы![]() и
и![]() ,
также эрмитовы.
,
также эрмитовы.
Решение.
Из решения задач 4 и 5 следует, что
линейному оператору![]() можно поставить в соответствие два
самосопряженных оператора:
можно поставить в соответствие два
самосопряженных оператора:
![]() ;
;![]()
Эрмитовость
операторов
![]() ,
,![]() и
равенство (5.1) приводят к эрмитовости
операторов
и
равенство (5.1) приводят к эрмитовости
операторов![]() и
и![]() :
:
![]() ;
;![]() .
.
Задача
7. Используя определение![]() (7.1)
(7.1)
и
свойство
![]() (7.2)
(7.2)
,
показать, что уравнение
![]() (7.3)
(7.3)
имеет
решение лишь для вещественного числа
![]() .
.
Решение. Подставляя
![]() ,
,
где
![]() -
решение уравнения (7.3), в определение
эрмитова оператора (7.1), запишем
-
решение уравнения (7.3), в определение
эрмитова оператора (7.1), запишем
![]() .
.
Используя
свойство (7.2), вынесем число
![]() ,
стоящее слева и справа от запятой, за
знак скалярного произведения. Это дает
,
стоящее слева и справа от запятой, за
знак скалярного произведения. Это дает
![]() .
.
Сокращая
на положительное число
![]() ,
получим
,
получим
![]() .
.
Задача
8. Доказать, что собственные функции
эрмитова оператора![]() с невырожденным дискретным спектром
ортогональны.
с невырожденным дискретным спектром
ортогональны.
Решение.В качестве функции![]() и
и![]() в определении
в определении![]() рассмотрим
рассмотрим![]() и
и![]() ,
являющиеся решениями уравнений
,
являющиеся решениями уравнений
![]() ,
,![]() (8.1)
(8.1)
соответственно.
Воспользуемся определением (7.1) эрмитова
оператора, записав его в форме
![]() .
.
Подставляя сюда правые части уравнений (8.1) и учитывая свойство (7.2), получим
![]() .
.
В силу
вещественности и невырожденности
собственных значений
![]() и
и![]() ,
отсюда найдем
,
отсюда найдем
![]() ;
;![]() ,
,![]() , (8.2)
, (8.2)
что и требовалось доказать.
Объединяя
равенства
![]() (8.4)
(8.4)
и (8.2), запишем условие ортонормированности
![]() (8.3)
(8.3)
собственных функций эрмитова оператора с невырожденным дискретным спектром.
Задача
9.Используя свойство ортонормированности
(8.2), найти коэффициенты![]() разложения произвольной функции
разложения произвольной функции![]() по базису в гильбертовом пространстве.
по базису в гильбертовом пространстве.
Решение.
В качестве базиса выберем собственные
функции оператора![]() ,
полученные решением уравнения (7.3) и
удовлетворяющие условию (8.3). Искомое
разложение представим в форме
,
полученные решением уравнения (7.3) и
удовлетворяющие условию (8.3). Искомое
разложение представим в форме
![]() ,
,
где
суммирование проводится по всем значениям
индекса
![]() (т.е по всем собственным значениям
(т.е по всем собственным значениям![]() оператора
оператора![]() ).
Для нахождения коэффициентов
).
Для нахождения коэффициентов![]() запишем скалярное произведение
запишем скалярное произведение
![]() .
.
Преобразуем
его с учетом свойств (7.2),
![]() ,
(8.3). Это дает
,
(8.3). Это дает
![]()
Таким образом, окончательно запишем
![]() ,
,![]() .
.
Коэффициент
![]() имеет смысл проекции функции
имеет смысл проекции функции![]() на орт
на орт![]() гильбертова пространства.
гильбертова пространства.
Задача 10.Решить уравнение (7.3) для оператора
![]() ,
,![]()
Решение.Из решения задачи 3(б) и равенств
![]() (10.1)
(10.1)
найдем
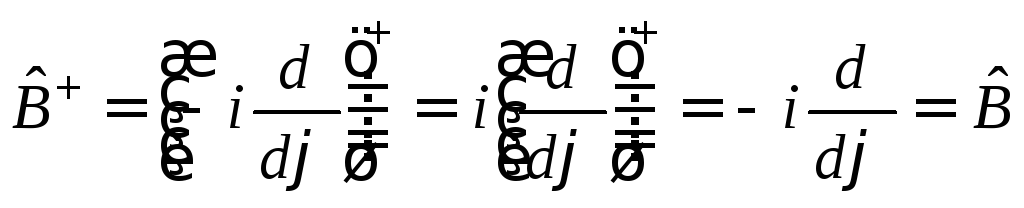 ,
,
т.е.
рассматриваемый оператор
![]() Эрмитов, а его собственные значения
вещественны. Уравнение (7.3) примет вид
Эрмитов, а его собственные значения
вещественны. Уравнение (7.3) примет вид
![]() .
.
Решая его, найдем
![]() .
.
Из условия периодичности (см. задачу 3(б))
![]()
вытекает равенство
![]() ,
,
из которого получаем ограничение
![]() ;
;![]()
Из
дискретности и невырожденности спектра
следует, что после нормировки (8.4) функции
![]() будут обладать свойством (8.3).
будут обладать свойством (8.3).
Запишем условие нормировки (8.4) в виде
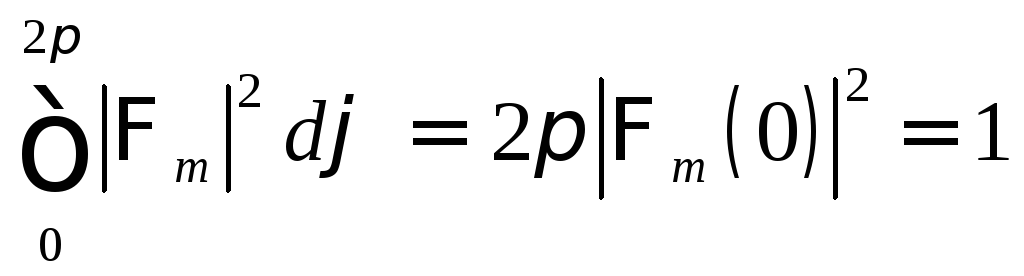
В общем случае постоянный множитель есть комплексное число, однако ввиду всегда допустимого введения произвольного фазового множителя
![]() ,
,![]() (10.1)
(10.1)
будем
предполагать вещественность константы
![]() .
Это дает
.
Это дает
![]()
Окончательно запишем
![]() ;
;![]()
Задача 11.Решить уравнение (7.3) для оператора
![]() ,
,![]() .
.
Решение. Из (10.1) и решения задачи 3а следует, что рассматриваемый оператор Эрмитов. Следовательно, его собственные значения вещественны. Уравнение (7.3) примет вид
![]() ,
,![]()
Решая его, найдем
![]() . (11.1)
. (11.1)
Норма
функции
![]() неограниченна, поскольку
неограниченна, поскольку
 .
.
Следовательно,
при соответствующем выборе константы
![]() функции
функции![]() и
и![]() вида (11.1) будут удовлетворять условию
вида (11.1) будут удовлетворять условию![]() .
(11.2)
.
(11.2)
Для
расчета
![]() воспользуемся равенством
воспользуемся равенством![]() .
Собственный дифференциал
.
Собственный дифференциал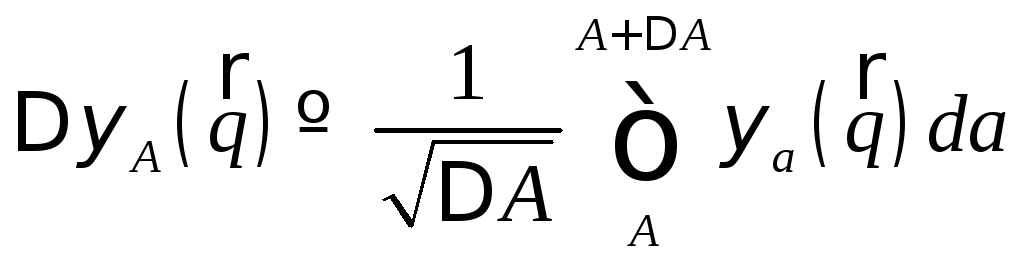 для функции (11.1) имеет вид
для функции (11.1) имеет вид
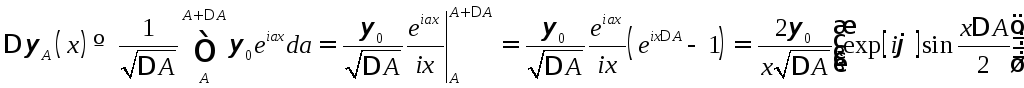
![]() .
.
Подставляя
![]() в определение нормы
в определение нормы![]() (11.3)
(11.3)
, приходим к интегралу
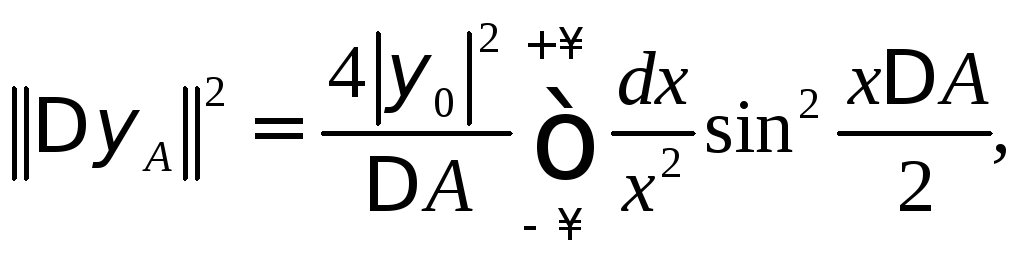
который после замены переменных
![]()
приводя к виду
![]()
Используя табличный интеграл

из условия нормировки получим
![]()
Как и
в задаче 10, константу нормировки
![]() выберем вещественной. Таким образом,
окончательно запишем
выберем вещественной. Таким образом,
окончательно запишем
![]() . (11.4)
. (11.4)
Задача 12.Для стационарного состояния вида
 (12.1)
(12.1)
описывающего
в одномерном случае частицу в бесконечно
глубокой потенциальной яме ширины
![]() ,
рассчитать средние значения величин,
соответствующих операторам:
,
рассчитать средние значения величин,
соответствующих операторам:
а)
![]()
б)
![]()
Решение.
а) По определению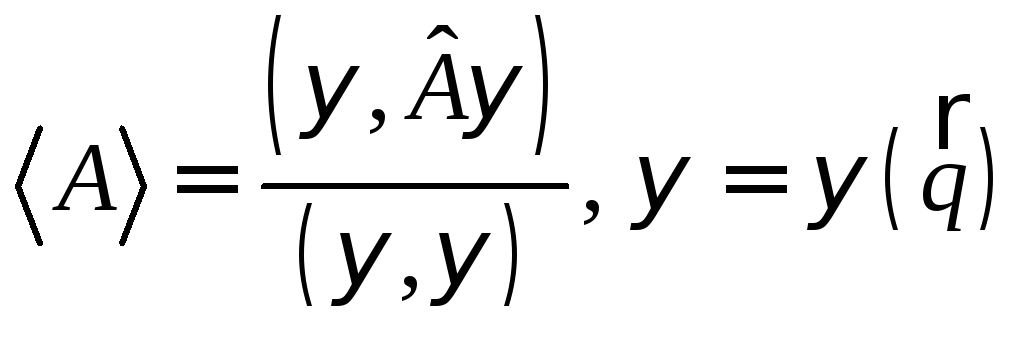 ,
(12.2)
,
(12.2)
запишем
![]() (12.3)
(12.3)
Расчет числителя (12.3) дает
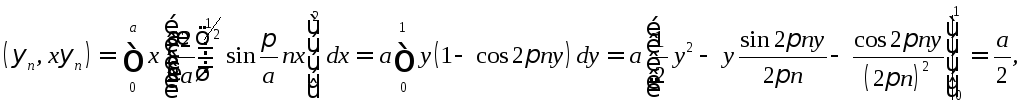
где использованы соотношения
![]()
Аналогичным образом для знаменателя (12.3) получим
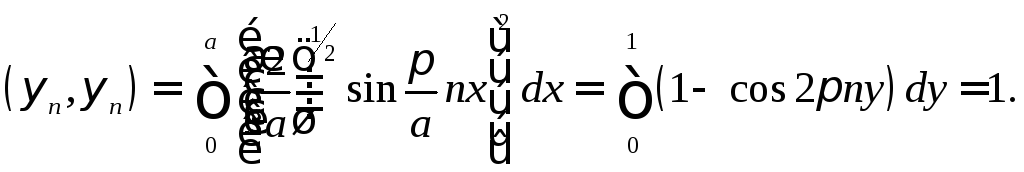
Следовательно,
для
![]() будем иметь
будем иметь
![]()
б) Учитывая свойство (7.2) и определение (12.2), запишем
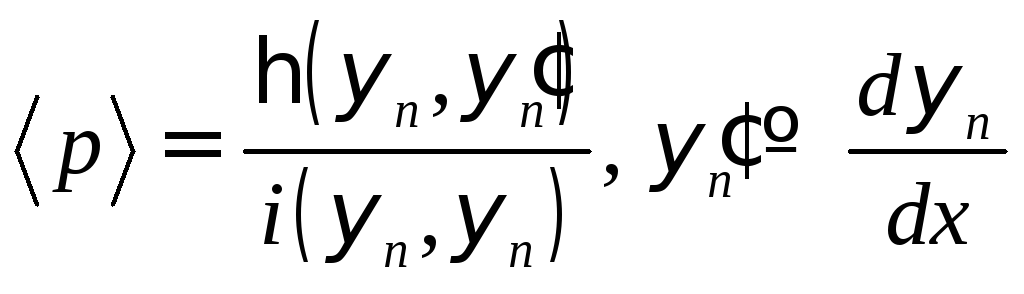 . (12.4)
. (12.4)
Расчет числителя (12.4) дает
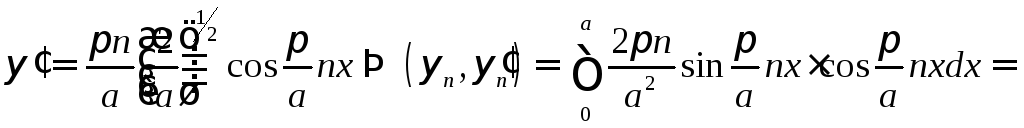
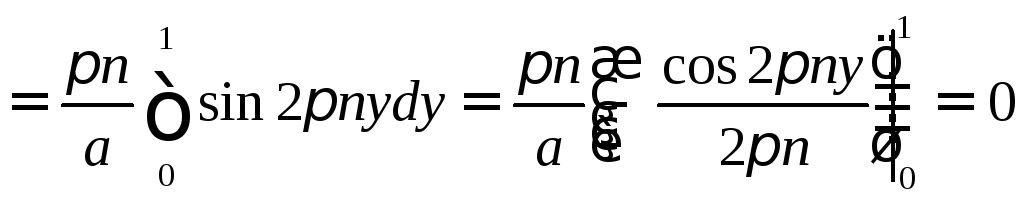
таким
образом, для
![]() будем иметь
будем иметь
![]()
Задача
13.В![]() -
представлении решить уравнение
-
представлении решить уравнение![]() (13.1)
(13.1)
для
оператора
![]() .
.
Решение.В одном случае имеем
![]() (13.2)
(13.2)
где
![]() -
некоторое собственное значение оператора
-
некоторое собственное значение оператора![]() .
Учитывая определения
.
Учитывая определения
![]() (13.6)
(13.6)
отсюда найдем
![]() (13.3)
(13.3)
Равенство
(13.3) возможно лишь при условии, что
![]() равна нулю всюду, кроме точки
равна нулю всюду, кроме точки![]() .
Среди решений уравнения (13.2) или (13.3) не
существует ни одной квадратично-интегрируемой
функции. Единственной функцией,
удовлетворяющей (13.2) и нормировке (11.2),
является дельта-функция, определенная
равенствами
.
Среди решений уравнения (13.2) или (13.3) не
существует ни одной квадратично-интегрируемой
функции. Единственной функцией,
удовлетворяющей (13.2) и нормировке (11.2),
является дельта-функция, определенная
равенствами
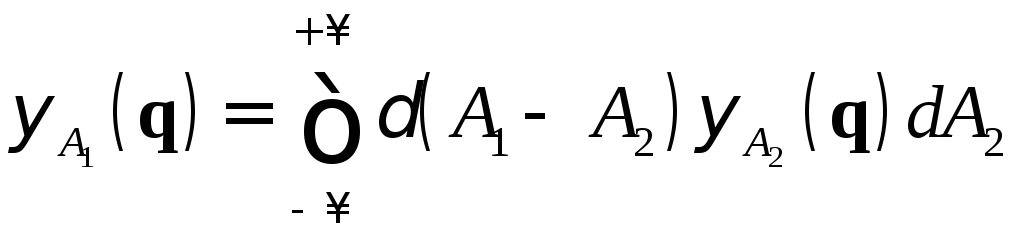 , (13.4)
, (13.4)
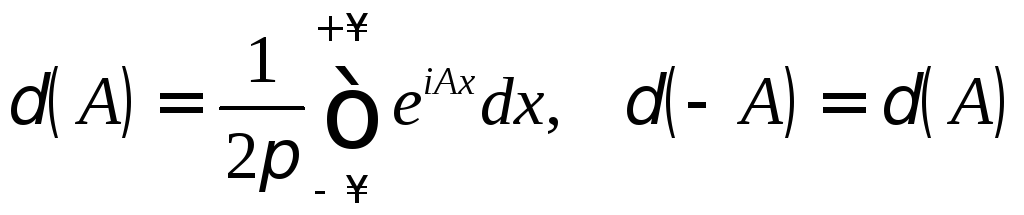 . (13.5)
. (13.5)
Таким
образом, функция
![]() имеет вид
имеет вид
![]() .
.
В трехмерном случае вместо (13.2) запишем
![]() . (13.7).
. (13.7).
В силу
(13.6) оператор
![]() представим в виде суммы трех коммутативных
операторов:
представим в виде суммы трех коммутативных
операторов:![]() .
Это обстоятельство позволяет для решения
уравнения (13.7) использовать метод
разделения переменны. Это дает
.
Это обстоятельство позволяет для решения
уравнения (13.7) использовать метод
разделения переменны. Это дает
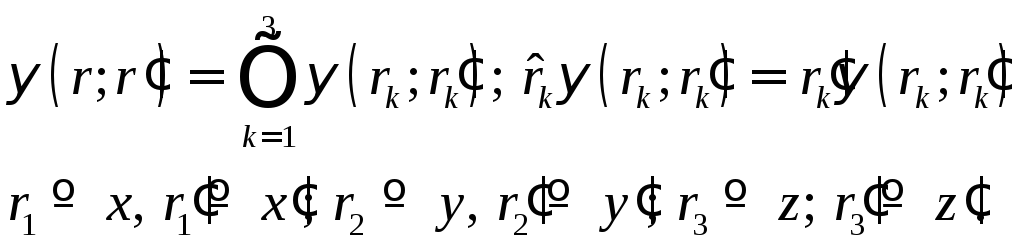 (13.8)
(13.8)
Решая (13.8) и учитывая равенство
![]() (13.9)
(13.9)
вытекающее
из определения дельта-функции в
![]() -
мерном пространстве векторов
-
мерном пространстве векторов![]() :
:
![]() , (13.10)
, (13.10)
для
![]() найдем
найдем
![]() .
.
Задача
14. В![]() -
представлении найти собственную функцию
оператора импульса.
-
представлении найти собственную функцию
оператора импульса.
Решение.Записывая![]() (14.1)
(14.1)
в декартовых координатах
![]() (14.2)
(14.2)
и
учитывая, что
![]() представим в форме суммы трех коммутативных
операторов (так же, как и
представим в форме суммы трех коммутативных
операторов (так же, как и![]() ),
),
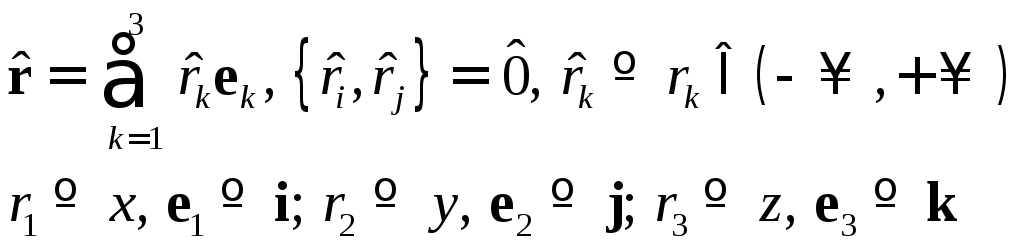 (14.3)
(14.3)
воспользуемся решением сходной одномерной задачи II. Уравнение (13.1) в обозначениях (14.3) принимает вид
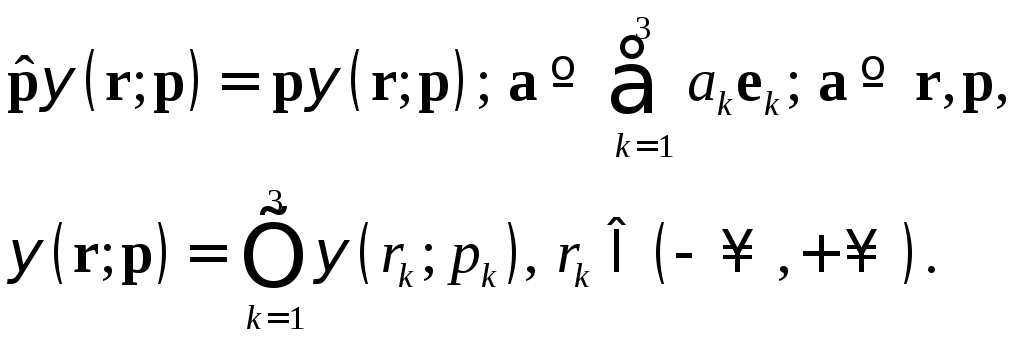 (14.4)
(14.4)
Уравнения
(14.4) сводятся к трем одномерным уравнениям
![]()
![]()
подобным исследованному в задаче II. Из (11.4) имеем
![]() (14.5)
(14.5)
Вещественная,
как и в (11.4), константа
![]() находится
из условия нормировки (11.2)
находится
из условия нормировки (11.2)
![]() (14.6)
(14.6)
Подставляя (14.5) в (14.6)

и проводя
под интегралом замену переменных
![]() ,
найдем
,
найдем
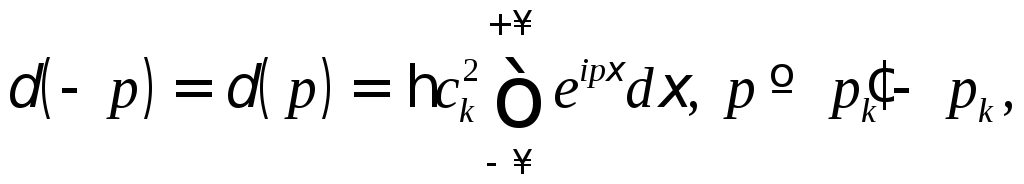
что с учетом (13.5) дает
![]()
Подставляя
найденную константу
![]() в (14.5) получим
в (14.5) получим
![]()
что вместе с (14.4) дает
![]() (14.7)
(14.7)
Условие ортонормированности (11.2) для собственной функции (14.7) оператора импульса с учетом (13.9) и (14.6) имеет вид
![]() (14.8)
(14.8)
Здесь
индексами 1 и 2 нумеруются различные
значения
![]() и
и![]() вектора
вектора![]() ,
тогда как в (14.4) эти же индексы используются
для обозначения проекций
,
тогда как в (14.4) эти же индексы используются
для обозначения проекций![]() и
и![]() вектора
вектора![]() на соответствующие оси декартовых
координат.
на соответствующие оси декартовых
координат.
Задача
15.В![]() -
представлении получить явный вид
оператора
-
представлении получить явный вид
оператора![]() ,
используя координаты а) декартовы; б)
сферические.
,
используя координаты а) декартовы; б)
сферические.
Решение.а) В декартовых координатах (14.3) и (14.2) имеем
![]() (15.1)
(15.1)
б)
Переход от декартовых координат
![]() к сферическим
к сферическим![]() определяется формулами:
определяется формулами:
![]() (15.2)
(15.2)
![]() (15.3)
(15.3)
Для
операторов
![]() и
и![]() переход (15.2) к сферическим координатам
дает
переход (15.2) к сферическим координатам
дает
![]()
Подставляя эти выражения в (15.1), запишем
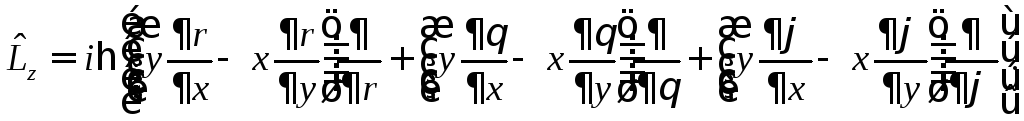 (15.4)
(15.4)
С учетом (15.3) произведенные сферических координат и выражения в круглых скобках (15.4) приводятся к виду
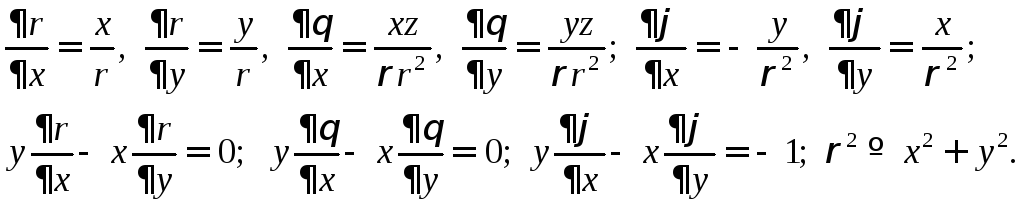 (15.5)
(15.5)
Подставляя
вторую строку (15.5) в (15.4), для оператора
![]() в сферических координатах получаем
в сферических координатах получаем
![]() (15.6)
(15.6)
Задача
16.В сферических координатах![]() -
представления найти собственную функцию
оператора
-
представления найти собственную функцию
оператора![]() .
.
Решение.
Оператор![]() (15.6)связан с оператором
(15.6)связан с оператором![]() задачи 10 равенством
задачи 10 равенством
![]()
Используя
решение задачи 10, для собственных функций
![]() ,
удовлетворяющих уравнению
,
удовлетворяющих уравнению
![]() (16.1)
(16.1)
(где
![]() -
собственное значение оператора
-
собственное значение оператора![]() ,
соответствующее
,
соответствующее![]() ),
получаем
),
получаем
![]() (16.2)
(16.2)
Задача
17. В![]() -
представлении (одномерная система)
решить уравнение (7.3) для оператора
-
представлении (одномерная система)
решить уравнение (7.3) для оператора![]() в случае частицы в бесконечно глубокой
потенциальной яме, ширины
в случае частицы в бесконечно глубокой
потенциальной яме, ширины![]() .
.
Решение. В случае бесконечно глубокой ямы по определению имеем
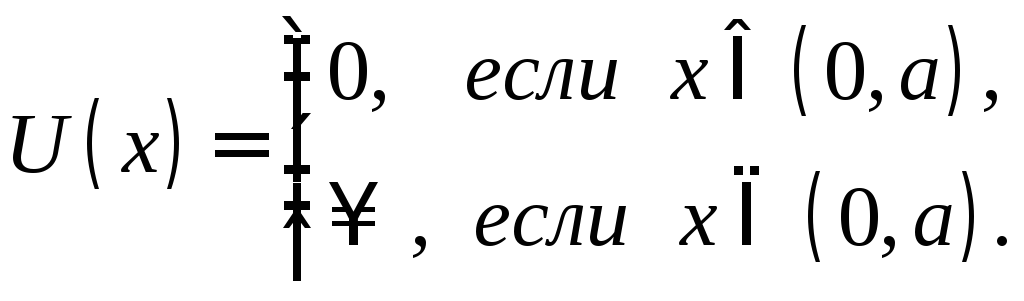 (17.1)
(17.1)
Интересующее
нас решение ищем на отрезке
![]() (17.2)
(17.2)
Поскольку
в точках
![]() и
и![]() потенциальная энергия частицы обращается
в бесконечность, вероятность преодоления
бесконечного барьера и попадания за
пределы области (17.2) равна нулю. Оказавшись
в области (17.2), частица все время будет
находиться в ней. Из формул
потенциальная энергия частицы обращается
в бесконечность, вероятность преодоления
бесконечного барьера и попадания за
пределы области (17.2) равна нулю. Оказавшись
в области (17.2), частица все время будет
находиться в ней. Из формул![]() (17.3)
(17.3)
и
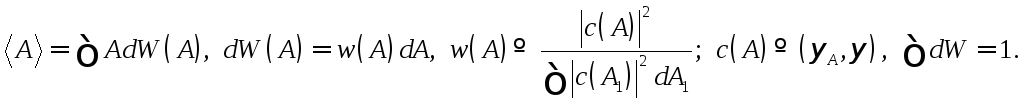 (17.4)
(17.4)
следуют соотношения
![]()
где
![]() -
волновая функция
-
волновая функция![]() ,
удовлетворяющая стационарному уравнению
Шредингера
,
удовлетворяющая стационарному уравнению
Шредингера
![]() (17.5)
(17.5)
совпадающему
с уравнением (13.1) или (13.2) (в зависимости
от характера спектра), т.е. функция
![]() ,
удовлетворяющая (17.5), есть собственная
функция
,
удовлетворяющая (17.5), есть собственная
функция![]() оператора
оператора![]() ,
соответствующая собственному значению
,
соответствующая собственному значению![]() .
Из сказанного вытекают граничные условия
.
Из сказанного вытекают граничные условия![]() ,
накладываемые на решение уравнения
(17.5).
,
накладываемые на решение уравнения
(17.5).
Таким образом, приходим к задаче
![]() (17.6)
(17.6)
Отсюда следует:
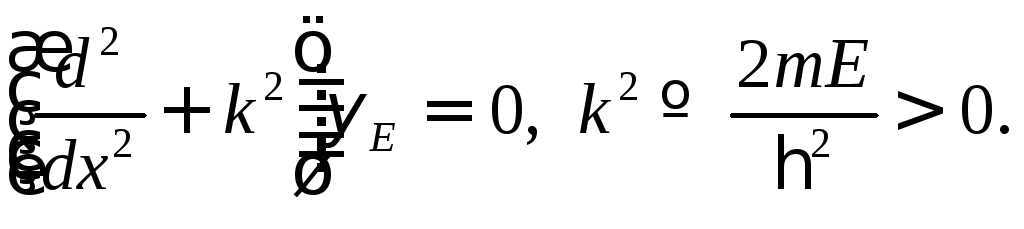 (17.7)
(17.7)
Положительность
собственного значения
![]() оператора
оператора![]() вытекает из положительности
вытекает из положительности![]() и
и![]() .
Решение уравнения (17.7) представимо в
виде суперпозиции двух элементарных
состояний, которые на языке
.
Решение уравнения (17.7) представимо в
виде суперпозиции двух элементарных
состояний, которые на языке![]() (17.3) интерпретируются как волны де Броля,
распространяющиеся в противоположных
направлениях оси
(17.3) интерпретируются как волны де Броля,
распространяющиеся в противоположных
направлениях оси![]() :
:
![]() (17.8)
(17.8)
Подстановка (17.8) в граничные условия (17.6) приводит к системе однородных уравнений
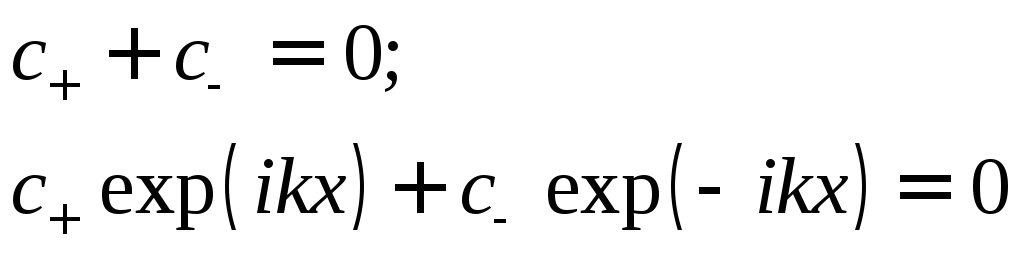 (17.9)
(17.9)
для
неизвестных коэффициентов
![]() .
Критерий существования тривиального
решения этой системы
.
Критерий существования тривиального
решения этой системы
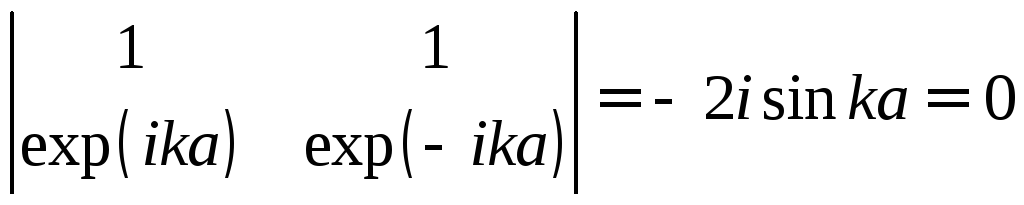
дает условие квантования
![]()
собственного
значения
![]() (17.5). Это означает, что
(17.5). Это означает, что![]() обладает
дискретным спектром, а уравнение (17.5)
эквивалентно (7.3). Вводя согласно (17.9)
обозначения
обладает
дискретным спектром, а уравнение (17.5)
эквивалентно (7.3). Вводя согласно (17.9)
обозначения
![]()
где
![]() -
пока неизвестная вещественная (в силу
наличия у
-
пока неизвестная вещественная (в силу
наличия у![]() произвольного фазового множителя
(10.1) это всегда возможно) константа, для
функции (17.8) будем иметь
произвольного фазового множителя
(10.1) это всегда возможно) константа, для
функции (17.8) будем иметь
![]() (17.10)
(17.10)
Поскольку
собственные функции оператора
![]() с дискретным спектром квадратично
интегрируемы, условие нормировки имеет
вид
с дискретным спектром квадратично
интегрируемы, условие нормировки имеет
вид
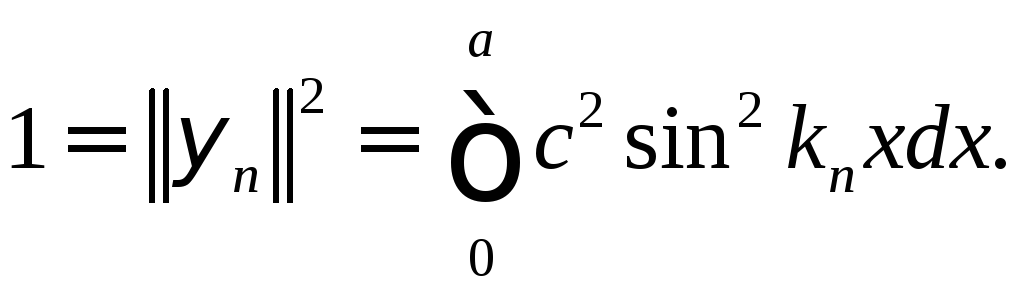
Отсюда с учетом решения задачи 12 находим
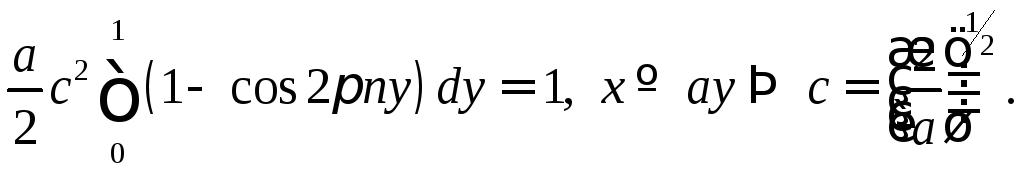
Подставляя найденное значение константы в (17.10), запишем решение задачи в окончательной форме
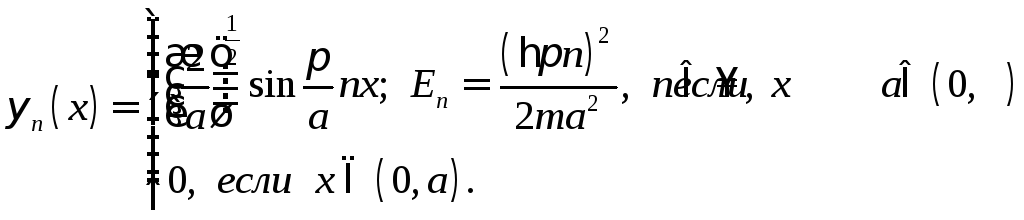 (17.11)
(17.11)
![]()
Задача
18. Используя формулы (17.4) и решения
задач 13 и 14, найти плотности вероятностей![]() и
и![]() для стационарного состояния
для стационарного состояния![]() (см. задачу 17).
(см. задачу 17).
Решение.
а) Согласно (17.3) амплитуда![]() разложения состояния
разложения состояния![]() по базису
по базису![]() равна
равна
![]()
В силу
нормировки
![]() на единицу из (17.4) и (17.11) найдем
на единицу из (17.4) и (17.11) найдем
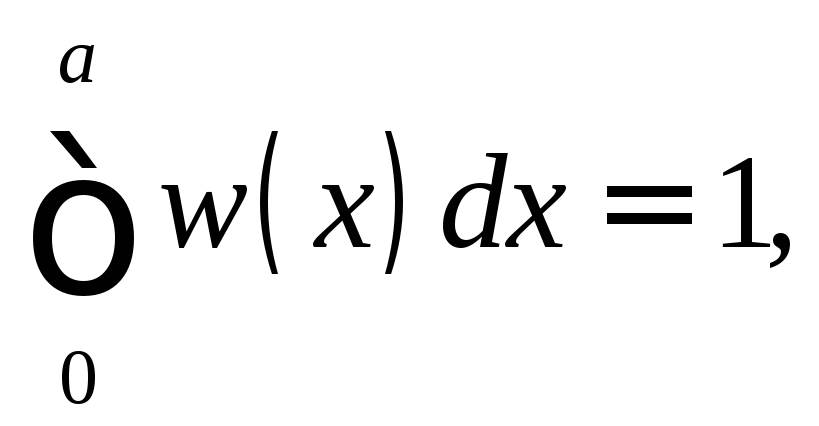
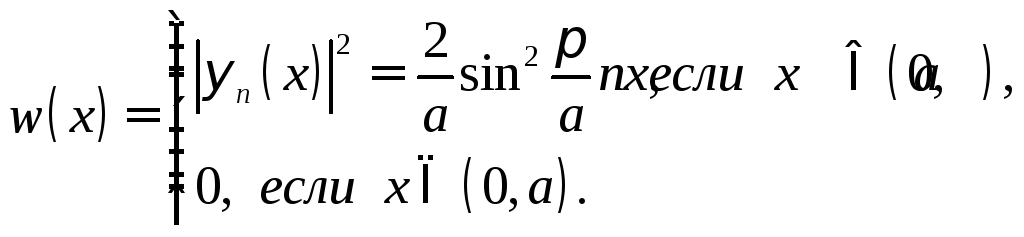 (18.1)
(18.1)
б)
Аналогично
![]() (18.2)
(18.2)
для
амплитуды
![]() разложения
разложения![]() по базису
по базису![]() запишем
запишем
![]()
Подставляя
сюда
![]() из (17.11), вводя обозначения
из (17.11), вводя обозначения
![]()
и проводя интегрирование, получим
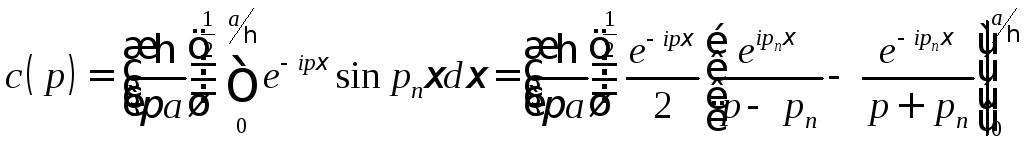 .
.
Учитывая равенства
![]()
для
![]() в (17.4) будем иметь
в (17.4) будем иметь
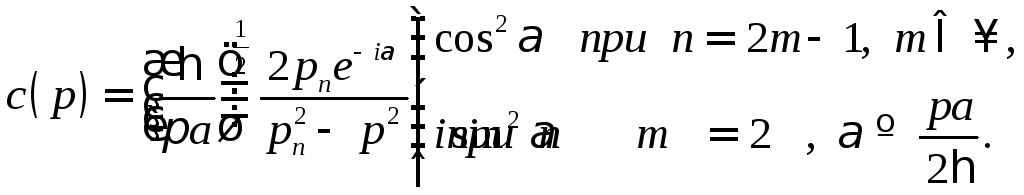
Подставляя
![]() в (17.4), запишем
в (17.4), запишем
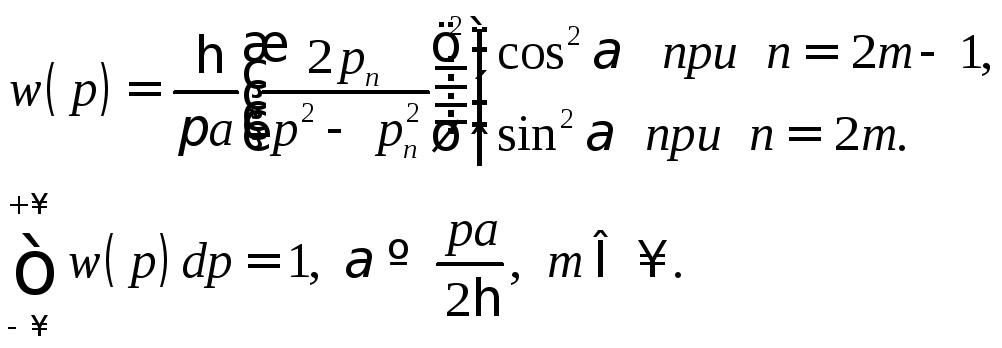 (18.3)
(18.3)
Условие нормировки в (18.3) вытекает из равенства Парсеваля в форме
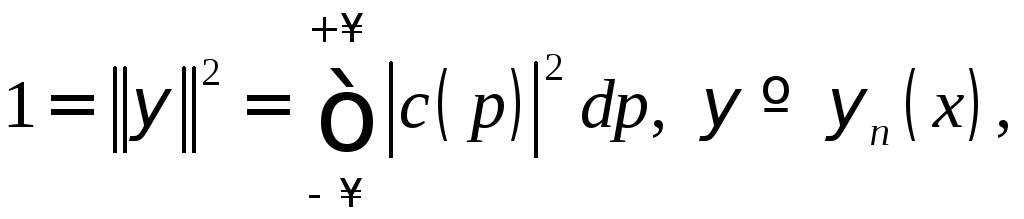
справедливой
в случае непрерывного спектра собственных
значений
![]() оператора
оператора![]() .
.
Задача
19. Рассчитать коммутатор![]() .
.
Решение.Для нахождения явного вида оператора![]() необходимо рассмотреть результат его
действия на произвольную функцию
необходимо рассмотреть результат его
действия на произвольную функцию![]() .
Используя (13.6), (14.2) и определение
.
Используя (13.6), (14.2) и определение![]() , (19.1)
, (19.1)
запишем
![]()
![]() . (19.2)
. (19.2)
Задача
20.Найти коммутатор![]() .
.
Решение.Используя (19.2) и вид![]() в
в![]() -
представлении
-
представлении
![]() , (20.1)
, (20.1)
запишем
![]() . (20.2)
. (20.2)
Задача
21.Показать, что![]() .
.
Решение.Воспользуемся соотношением
![]() , (21.1)
, (21.1)
легко проверяемым непосредственной подстановкой всех коммутаторов в (21.1) согласно определению (19.1).
Тогда для искомого коммутатора запишем
![]() . (21.2)
. (21.2)
Ввиду
симметричности (относительно перестановки
индексов) оператора
![]() и антисимметричности (согласно определению
(20.1)) тензора
и антисимметричности (согласно определению
(20.1)) тензора![]() двойное суммирование в (21.2) по индексам
двойное суммирование в (21.2) по индексам![]() и
и![]() дает нуль. Равенство
дает нуль. Равенство
![]() (21.3)
(21.3)
объясняется также и тем, что скалярный оператор инвариантен относительно преобразования
![]() . (21.4)
. (21.4)
Задача
22. Используя неравенство
Коши-Шварца-Буняковского получить
нижнюю границу для дисперсии![]() наблюдаемой
наблюдаемой![]() .
.
Решение.Выбирая в качестве![]() и
и![]() функции
функции
![]()
и используя неравенство
![]() , (22.1)
, (22.1)
получим
![]() . (22.2)
. (22.2)
В силу
эрмитовости
![]() оператор
оператор![]() так же эрмитов (7.1), т.е. выполняется
равенство
так же эрмитов (7.1), т.е. выполняется
равенство
![]() . (22.3)
. (22.3)
Согласно определению (13.5) неравенство (22.2) принимает вид
![]() .
.
Отсюда с учетом
![]() (22.4)
(22.4)
![]() (22.5)
(22.5)
получим
![]() .
.
Таким
образом, мы нашли, что наименьшее из
возможных значений дисперсии
![]() (и среднеквадратичного отклонения
(и среднеквадратичного отклонения![]() )
физической величины
)
физической величины![]() равно нулю.
равно нулю.
Задача
23.Доказать, что![]() обращается в нуль, если соотношение, по
которому проводится усреднение,
описывается собственной функцией
оператора
обращается в нуль, если соотношение, по
которому проводится усреднение,
описывается собственной функцией
оператора![]() .
.
Решение.
Пусть в качестве![]() в (13.5) выбрана
в (13.5) выбрана![]() ,
удовлетворяющая (7.3). Тогда в силу
,
удовлетворяющая (7.3). Тогда в силу
![]() , (23.1)
, (23.1)
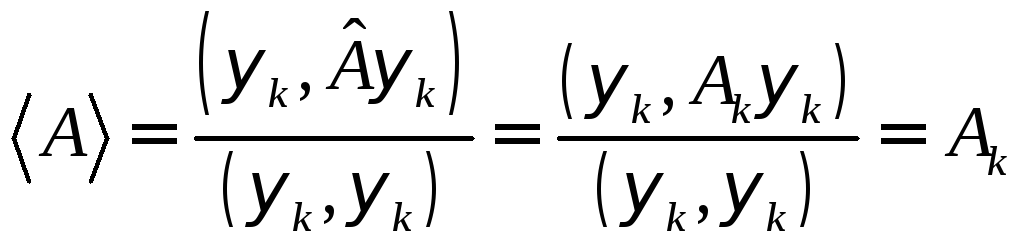 (23.2)
(23.2)
и (13.5) запишем
![]() .
.
С учетом определения (22.5) и равенства (22.3) это дает
![]() .
.
Верно и обратное: равенство нулю нормы некоторой функции
![]()
реализуется лишь в случае равенства нулю этой функции:
![]() . (23.3)
. (23.3)
Сравнивая
равенство (23.3) с уравнением (7.3), заключаем,
что оно возможно, если
![]() -
одна из собственных функций оператора
-
одна из собственных функций оператора![]()
![]() ,
,
где
![]() -
собственное значение оператора
-
собственное значение оператора![]() ,
соответствующее этой собственной
функции.
,
соответствующее этой собственной
функции.
Задача
24.Для стационарного состояния (17.11)
рассчитать![]() и
и![]() (см.
задачу 12).
(см.
задачу 12).
Решение.Согласно определению![]() (24.1)
(24.1)
запишем
![]() . (24.2)
. (24.2)
Для
получения
![]() и
и![]() (с учетом
(с учетом![]() (24.3) и
(24.3) и![]() (24.4) нам остается рассчитать
(24.4) нам остается рассчитать![]() и
и![]() .
По определению (13.5) для
.
По определению (13.5) для![]() имеем
имеем
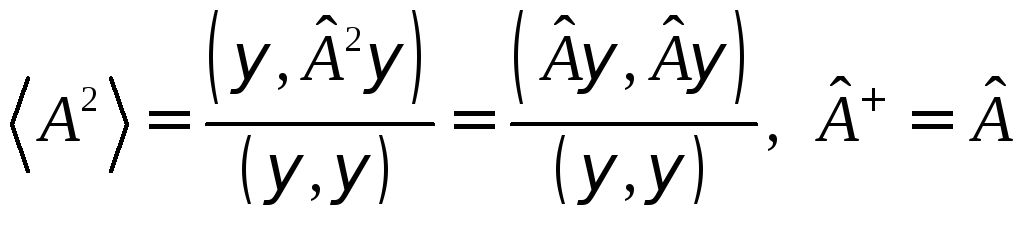 . (24.5)
. (24.5)
а) В
случае
![]() число
число![]() находится вычислениями
находится вычислениями
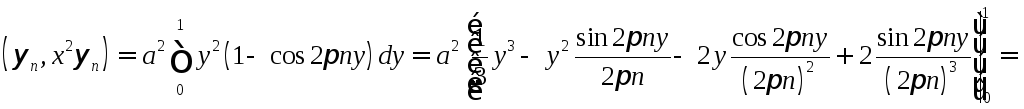
![]() ,
,
подобными проделанным в задаче 12а. Следовательно,
![]() . (24.6)
. (24.6)
Подставляя (24.6) и (24.3) в (24.2), получим
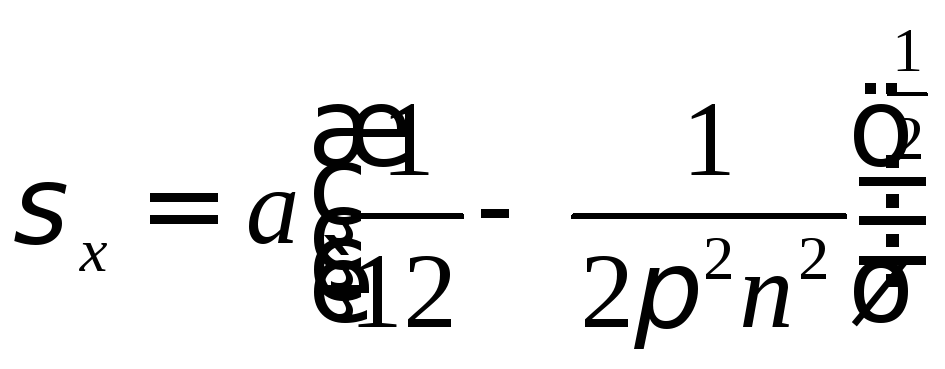 . (24.7)
. (24.7)
б) Для
оператора
![]() (см. задачу 12б) найдем
(см. задачу 12б) найдем
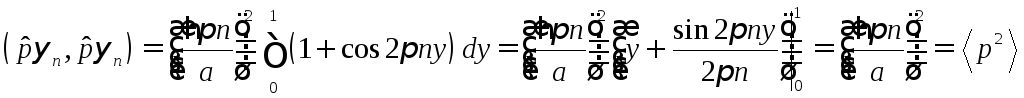 . (27.8)
. (27.8)
Подстановка (24.8) и (24.4) в (24.2) дает
![]() . (24.9)
. (24.9)
