Итак, наилучшая средняя квадратическая аппроксимация функции 
заданной на сфере, многочленом, составленным из нормированных сферических гармоник степени и порядка 
, имеет вид
(4.17)
где -- нормированная присоединенная функция Лежандра.
Специальное исследование показало, что наш ряд при неограниченном увеличении числа членов при некоторых дополнительных условиях, накладываемых на функцию
, сходится. Однако, исследование скорости этой сходимости лежит за пределами нашего курса.
4.3.1 Интегральная форма ряда Лапласа
Мы уже говорили, что разложения вида (4.17) есть аналог ряда Фурье, в котором роль тригонометрических функций выполняют сферические функции. Существует также и аналог интеграла Фурье -- интегральная форма ряда Лапласа. Для того,
чтобы ее получить, подставим в (4.17) постоянные 
и 
, которые определятся с помощью интегралов (4.16). Переменные, по которым производится интегрирование мы будем помечать штрихом. Таким образом
Принимая во внимание, что
получим
(4.18)
Для дальнейшего упрощения полученной интегральной формулы воспользуемся так называемой теоремой сложения сферических функций.
Пусть точка 
имеет постоянные координаты, а точка 
принадлежит элементу поверхности и имеет штрихованные координаты. Обозначим центральное
расстояние между этими двумя точками греческой буквой 
. Тогда теорема сложения для нормированных сферических функций выглядит так
(4.19)
Теперь формулу (4.18) можно переписать следующим образом
(4.20)
Каждое слагаемое в полученной формуле часто называют функциями Лапласа
(4.21)
Лекция 5. Аналитическое представление гравитационного потенциала
•5.1 Разложение гравитационного потенциала в ряд Лапласа
•5.2 Посточнные Стокса
•5.3 Механический смысл стоксовых постоянных
•5.4 Потенциал тяжести
•5.5 Пределы Пуанкаре и Крудели для угловой скорости вращения. Фигуры равновесия
5.1 Разложение гравитационного потенциала в ряд Лапласа
Напомним, что под потенциалом какой либо силы, в том числе и силы тяжести мы будем понимать силовую функцию. Для начала остановимся на потенциале сил притяжения, который чаще всего называют гравитационным потенциалом. Пусть
элемент массы dm находится в точке Q 
, а точка P(x,y,z) с фиксированными координатами находится вне притягивающего тела. Радиус-вектор, соединяющий точки Р и Q, будем обозначать через 
, а радиус-векторы этих точек соответственно
через 
и . Угол между этими векторами будем обозначать через . Если точка О - - начало координат, то из треугольника ОРQ следует
Потенциал притяжения тела в точке 
имеет вид
(5.1)
где 
-- элемент объема, 
-- плотность. Вынесем из-под знака корня величину
, получим
Под знаком интеграла стоит производящая функция полиномов Лежандра (см. формулу (4.1)), поэтому
где 
-- полином Лежандра степени 
.
Теперь потенциал притяжения в точке 
принимает вид
(5.2)
Каждое отдельное слагаемое полученной формулы есть функция Лапласа для
потенциала притяжения во внешней точке. Обозначив ее через 
, получим
(5.3)
Теперь ряд Лапласа можно записать так
(5.4)
Функции Лапласа, как следует из формулы (5.3), зависят от распределения плотности внутри притягивающего тела. Приведенный интеграл есть постоянная величина, которая, в свою очередь, определяется с помощью так называемых постоянных Стокса, или, стоксовых постоянных.
5.2 Посточнные Стокса
Постоянной Стокса называется величина, которая определяется следующим образом
(5.5)
где гармоническая функция внутри объема интегрирования.
Вернемся к формуле (5.3). Воспользуемся формулой сложения гармонических функций (4.19). Ее, очевидно, можно переписать следующим образом
Следовательно
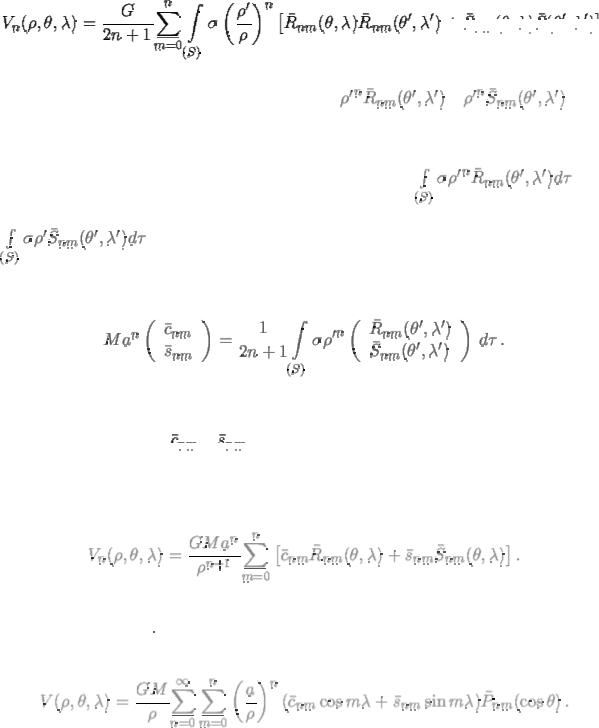
(5.6)
Функции текущих (штрихованных) координат |
и |
являются |
||
гармоническими, так как они принадлежат к шаровым функциям первого типа. |
||||
Следовательно, по определению (5.5) интегралы вида |
|
и |
||
являются стоксовыми постоянными. |
|
|
||
Введем обозначения |
|
|
||
|
|
|
|
(5.7) |
|
|
|
|
|
Здесь, как несколько позже убедимся, М -- масса тела, а -- постоянная, имеющая
размерность длины, а 
и 
безразмерные постоянные Стокса. Теперь функцию Лапласа для потенциала притяжения во внешней точке Можно представить следующим образом
(5.8)
Суммируя по всем 
, получим искомое разложение потенциала притяжения в ряд Лапласа
(5.9)
Все рассуждения мы провели для нормированных функций, отмечая их чертой сверху. Однако эти же рассуждения справедливы и для ненормированных функций. В этом случае постоянные Стокса будут иметь несколько иной вид. Опуская выкладки, приведем лишь окончательную формулу