
- •Теория фигуры Земли
- •В.Л.Пантелеев
- •Лекция 1. Теория фигуры Земли
- •Краткий исторический обзор
- •Лекция 2. Геодезические системы координат
- •2.1 Декартовы системы координат
- •2.2 Сферическая система координат
- •2.3 Геодезическая система координат
- •2.4 Эллипсоидальная система координат
- •Лекция 3. Основные формулы теории потенциала
- •3.1 Формулы Грина
- •3.1.1 Формула Остроградского
- •3.1.2 Первая формула Грина
- •3.1.3 Вторая формула Грина
- •3.1.4 Третья формула Грина
- •3.2 Гармонические функции
- •3.2.1 Свойства гармонических функций
- •3.2.2 Теоремы о гармонических функциях
- •3.3 Шаровые функции
- •3.3.1 Дифференциальное уравнение для сферических функций
- •3.3.2 Интегрирование дифференциального уравнения
- •Лекция 4. Сферические функции
- •4.1 Полиномы Лежандра и их свойства
- •4.1.1 Ортогональность сферический функций
- •4.2 Нормированные сферические функции
- •4.3.1 Интегральная форма ряда Лапласа
- •5.1 Разложение гравитационного потенциала в ряд Лапласа
- •5.2 Посточнные Стокса
- •5.3 Механический смысл стоксовых постоянных
- •5.4 Потенциал тяжести
- •Лекция 6. Нормальная Земля
- •6.1 Нормальный потенциал тяжести
- •6.2 Сфероид Клеро
- •6.3 Теорема Стокса
- •6.4 Гравитационный потенциал эллипсоида вращения
- •Лекция 7. Нормальное поле тяжести Земли
- •7.1 Формула Сомильяны
- •7.2 Нормальная сила тяжести
- •7.3 Вторые производные гравитационного потенциала
- •Лекция 8. Определение фигуры геоида
- •8.1 Возмущающий потенциал
- •8.2 Краевая задача Дирихле для сферы
- •8.2.1 Внутренняя проблема Дирихле
- •8.3 Краевые задачи Неймана
- •8.4 Смешанная краевая задача
- •8.5 Определение высот геоида
- •8.6 Определение уклонений отвеса
- •Лекция 9. Квазигеоид Молоденского
- •9.1 Критика классической теории Стокса
- •9.2 Система высот
- •9.3 Краевые условия задачи Молоденского

пунктов задают геодезическими координатами 




 , соответственно, широтой, долготой и высотой. Фундаментально задачей является определение центра общего земного эллипсоида относительно центра масс.
, соответственно, широтой, долготой и высотой. Фундаментально задачей является определение центра общего земного эллипсоида относительно центра масс.
В доспутниковую эпоху геодезические работы вполне удовлетворяла привязка к эллипсоиду, аппроксимирующему исследуемую территорию. Советский геодезист Ф.М.Красовский получил параметры эллипсоида для Советского Союза с началом отсчета высот по Кронштадскому футштоку. Сжатие эллипсоида Красовского равно 1:298,3, Эта величина значительно отличалась от сжатия общего земного эллипсоида принятого в то время и полученного по гравиметрическим данным. Авторы давали разные оценки сжатия от 1:296,6 до 1:297,4. Первое же определение сжатия по спутниковым данным дало величину, практически совпадающую со сжатием эллипсоида Красовского. Точность определения существенно возросла. Генеральная Ассамблея МАС в 1976 г для сжатия Земли утвердила значение
1:298,2570.
Спутниковые альтиметрические исследования дали прямые измерения топографии
водной глади поверхности океанов, которая совпадает с геоидом с точностью 




 м. Сами альтиметрические наблюдения достигли точности нескольких сантиметров. Появилась необходимость с такой же точностью строить и теорию движения спутников и определять поверхность геоида. Классическое линейное приближение с точностью до первой степени сжатия стало неприемлемым. Если радиус Земли равен R, то малыми величинами мы должны считать линейные величины
м. Сами альтиметрические наблюдения достигли точности нескольких сантиметров. Появилась необходимость с такой же точностью строить и теорию движения спутников и определять поверхность геоида. Классическое линейное приближение с точностью до первой степени сжатия стало неприемлемым. Если радиус Земли равен R, то малыми величинами мы должны считать линейные величины 







 км. Малыми величинами второго порядка будут
км. Малыми величинами второго порядка будут 







 м, а третьего порядка --
м, а третьего порядка --
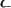







 см. Отсюда следует, что теория движения спутников должна обеспечивать сантиметровую точность, а современная теория фигуры Земли должна строиться так, чтобы обеспечить точность до малых третьего порядка. К сожалению, таких точностей еще не получено.
см. Отсюда следует, что теория движения спутников должна обеспечивать сантиметровую точность, а современная теория фигуры Земли должна строиться так, чтобы обеспечить точность до малых третьего порядка. К сожалению, таких точностей еще не получено.
Лекция 2. Геодезические системы координат
•2.1 Декартовы системы координат
•2.2 Сферическая система координат
•2.3 Геодезическая система координат
•2.4 Эллипсоидальная система координат

Сферическая система. Широта долгота и радиус-вектор. Система координат, построенная на эллипсоиде. Геодезические координаты: широта, долгота и высота. Связь между сферической,геодезической и декартовой системами координат.
Геодезические задачи решают на плоскости, если размеры площади невелики. Если исследуемая часть поверхности занимает несколько градусов широты или долготы, то необходимо учитывать и кривизну поверхности. В этом случае часто подходит и шар. Для решения глобальных задач, в том числе и задач по космической геодезии в качестве тела отсчета берут эллипсоид вращения. В частности на эллипсоиде решают следующие задачи:
--Уточнение формы и размеров общего земного эллипсоида (ОЗЭ).
--Перенос направлений и расстояний с физической поверхности на эллипсоид.
--Определение координат точек на поверхности референц-эллипсоида.
--Определение расстояний между точками с заданными координатами.
--Уточнение координат по мере уточнения элементов эллипсоида.
2.1 Декартовы системы координат
Введем две прямоугольные системы координат: локальную и глобальную.
Начало системы отсчета (точка Р) для локальной прямоугольной системы координат выберем в точке наблюдения, лежащей на поверхности эллипсоида. Ось РХ
направим на Север, ось РУ? на Восток, а ось |
по нормали к |
поверхности |
эллипсоида вниз (по внутренней нормали). |
В этой системе |
координат |
"горизонтальная" плоскость ХРУ не совпадает с плоскостью астрономического горизонта.
Глобальную декартову геодезическую систему координат Oxyz строят так: начало отсчета совмещают с центром ОЗЭ (не путать с центром масс Земли!), плоскость xOy -- c плоскостью экватора. Ось Ox совмещают с линией пересечения плоскости нулевого меридиана и плоскости экватора. Ось Oy пересекает экватор в точке с долготой 90°. Ось Oz совпадает с осью вращения ОЗЭ. Эта ось не обязательно совпадает с осью вращения Земли. Для трехосного ОЗЭ начало координат берут в центре масс Земли, а оси -- совпадающими с главными осями

инерции. В этом случае плоскость xOy, вообще говоря, не будет лежать в плоскости экватора.
2.2 Сферическая система координат
Телом отсчета для сферической системы координат является сфера с радиусом 

 . Начало этой системы координат совмещают с центром сферы. Координатами являются геоцентрическая широта
. Начало этой системы координат совмещают с центром сферы. Координатами являются геоцентрическая широта 

 , долгота
, долгота 
 и радиус-вектор
и радиус-вектор 
 . Широтой называется угол между радиусом-вектором и плоскостью экватора. Долгота есть угол между плоскостью, проходящей через заданную точку и осью вращения (плоскость меридиана) и плоскостью меридиана, принятого в качестве нулевого. Связь между сферической системой и глобальной декартовой определяется формулами
. Широтой называется угол между радиусом-вектором и плоскостью экватора. Долгота есть угол между плоскостью, проходящей через заданную точку и осью вращения (плоскость меридиана) и плоскостью меридиана, принятого в качестве нулевого. Связь между сферической системой и глобальной декартовой определяется формулами
(2.1)
В том случае, когда широта определяется как угол между плоскостью экватора и отвесной линией, сферическая система координат называется астрономической.
Широта и долгота, определенные в этой системе мы будем обозначать через 
 и
и 
 .
.
2.3 Геодезическая система координат
С геодезической системой координат 




 связывают понятия геодезической широты, долготы и высоты. Геодезическая широта В есть угол, под которым пересекается нормаль к поверхности эллипсоида с плоскостью экватора. Долгота
связывают понятия геодезической широты, долготы и высоты. Геодезическая широта В есть угол, под которым пересекается нормаль к поверхности эллипсоида с плоскостью экватора. Долгота  - - двугранный угол между плоскостью нулевого меридиана и плоскостью меридиана, проходящего через заданную точку.
- - двугранный угол между плоскостью нулевого меридиана и плоскостью меридиана, проходящего через заданную точку.
Геодезические широта и долгота отличаются от соответствующих астрономических координат, связанных с отвесной линией, так как отвесная линия не совпадает с нормалью к эллипсоиду. Отклонение отвесной линии можно спроецировать на две плоскости: плоскость меридиана и плоскость первого вертикала. Нетрудно понять,

что обе эти составляющие можно определить через разности между астрономическими и геодезическими координатами
(2.2)
Отклонения отвесной линии составляют, как правило, первые несколько секунд дуги. Заметим, что геодезическая и геоцентрическая долготы совпадают. Обе они определены как двугранный угол между плоскостью нулевого меридиана и плоскостью, содержащей ось вращения и заданную точку. Геоцентрическая же широта отличается от геодезической.
Рассмотрим точку 
 , лежащую вне ОЗЭ. Опустим из этой точки перпендикуляр на поверхность эллипсоида и продолжим его до пересечения с экваториальной плоскостью (рис. 2). Проекцию точки
, лежащую вне ОЗЭ. Опустим из этой точки перпендикуляр на поверхность эллипсоида и продолжим его до пересечения с экваториальной плоскостью (рис. 2). Проекцию точки 
 на поверхность эллипсоида обозначим через
на поверхность эллипсоида обозначим через

 Тогда отрезок PQ есть геодезическая высота точки
Тогда отрезок PQ есть геодезическая высота точки 
 . Угол, под которым упомянутый перпендикуляр пересекает плоскость экватора, есть геодезическая
. Угол, под которым упомянутый перпендикуляр пересекает плоскость экватора, есть геодезическая
широта 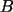 . Она относится как к точке
. Она относится как к точке  , так и к точке
, так и к точке 
 . Геоцентрические широты этих двух точек, как видно из рисунка, различаются. Геоцентрическая широта точки
. Геоцентрические широты этих двух точек, как видно из рисунка, различаются. Геоцентрическая широта точки
 угол
угол 

 между радиус-вектором этой точки и плоскостью экватора.
между радиус-вектором этой точки и плоскостью экватора.

|
|
Рис. 2. |
|
|
|
Установим связь между координатами точки , |
сжатием эллипсоида |
и широтами |
|||
и . Поскольку точка |
лежит на поверхности эллипсоида, то ее прямоугольные |
||||
координаты |
подчиняются |
уравнению |
эллипсоида |
вращения: |
|
|
. Рассмотрим сечение |
. |
Тогда, как |
легко видеть, |
|
. Чтобы определить |
, нужно найти угловой коэффициент нормали в |
||||
точке . Уравнение нормали к кривой |
|
в точке |
имеет вид |
||
|
|
|
|
|
(2.3) |

У нас |
, поэтому |
, |
,
Следовательно,
Определим отличие геоцентрической широты 

 от геодезической
от геодезической  . Имеем очевидные равенства
. Имеем очевидные равенства
(2.4)
Второй эксцентриситет эллипса, как мы знаем, определяется следующим образом
, поэтому
Для Земли второй эксцентриситет мал, поэтому, пренебрегая малыми второго порядка относительно сжатия, получим 








 . Можно также считать, что
. Можно также считать, что
Учитывая сказанное, получим
Наибольшее отличие геодезической широты от геоцентрической достигается на
широте 45° и составляет .
Связь глобальных декартовых координат с геоцентрическими определяется формулами (2.1). Определим теперь формулы, связывающие декартовы координаты с геодезическими. Это означает, что бы должны определить координаты точки 
 через параметры эллипсоида и геодезические широту и долготу.
через параметры эллипсоида и геодезические широту и долготу.

Поскольку 


 , для определения координат
, для определения координат 
 ,
, 
 ,
, 

 точки
точки 
 достаточно, для начала, определить только координаты
достаточно, для начала, определить только координаты 
 и
и 

 , то есть все рассуждения проводить
, то есть все рассуждения проводить
только для сечения |
. Обратимся к рис. 3. |
Рис. 3.
Определим прямоугольные координаты точки 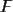
 , расположенной на высоте Н над поверхностью эллипсоида. Сначала определим координаты проекции точки
, расположенной на высоте Н над поверхностью эллипсоида. Сначала определим координаты проекции точки 
 на
на
поверхность эллипсоида (точка  ). Ее координаты в сечении Охz равны
). Ее координаты в сечении Охz равны
Индексом "0" мы отметили принадлежность координат к точке, лежащей на поверхности эллипсоида. Как мы видели
поэтому

Остается определить радиус-вектор точки  . Воспользуемся уравнением эллипса и выполним необходимые преобразования.
. Воспользуемся уравнением эллипса и выполним необходимые преобразования.
(2.5)
Выразим 




 и
и 



 через
через 




 и
и 



 , для чего воспользуемся приведенными
, для чего воспользуемся приведенными
выше формулами. Определим радиус-вектор точки 
следовательно,
(2.6)
Обозначим
(2.7)
Теперь
(2.8)
Для произвольного сечения, проходящего через ось вращения |
, будем иметь |
(2.9)
Теперь поднимем точку  на высоту Н и совместим ее с точкой
на высоту Н и совместим ее с точкой 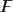
 . Прямоугольные координаты изменятся на
. Прямоугольные координаты изменятся на
