Поскольку интегрирование ведется по сфере радиуса в формуле (8.16) мы

полагали . Введем обозначение

(8.17)

и решение задачи Стокса принимает окончательный вид

(8.18)

Функцию часто называют функцией Стокса. В (8.17) она задана в виде разложения по степеням полиномов Лежандра от косинуса центрального расстояния

. Ее "компактный" вид следующий

Легко видеть, что точка -- особая. Здесь функция Стокса обращается в бесконечность, тем не менее интеграл (8.18) сходится, но при выполнении двух указанных выше условий, которым должны удовлетворять гравитационные аномалии. Используя формулу (8.1), которую часто называют формулой Брунса, из возмущающего потенциала легко получить высоты геоида

(8.19)

8.6 Определение уклонений отвеса

Отвесная линия (вертикаль) совпадает с направление вектора силы тяжести g.

Она является нормалью к уровенной поверхности. С другой стороны нормаль к эллипсоиду совпадает с направлением вектора нормальной силы тяжести. Эти две нормали не совпадают. Между ними образуется угол, который геодезисты называют

уклонением отвеса. Не будет ошибкой сказать и отклонение отвесной линии. Правда возникает вопрос отклонение от чего? Чтобы таких вопросов не возникало, мы будем употреблять геодезический термин.

Две упомянутые нормали, продолженные вверх, пересекаются с воображаемой небесной сферой в точках, одна из которых будет астрономическим зенитом (или просто зенитом), а другая -- геодезическим. Понятно, что и плоскости горизонта астрономического и геодезического не совпадают. Договорились считать уклонения отвеса положительным, если зенит смещается в северном или восточном направлении.

Обратимся к локальной геодезической системе координат с началом в пункте наблюдений (точка ). Горизонтальные оси PX и PY, как мы знаем из лекции 7, лежат в плоскости, перпендикулярной к нормали к эллипсоиду. Одна из них направлена на север, другая -- на восток. Ось PZ направлена вниз по внутренней нормали к эллипсоиду. Нетрудно понять, что при положительных "горизонтальных" компонентах вектора силы тяжести обе компоненты уклонения отвеса будут отрицательны. Поэтому компоненты уклонения отвеса в плоскости меридиана и первого вертикала соответственно определяют следующим образом

(8.20)

Из приведенных формул видно, что обе компоненты -- безразмерные величины, хотя на практике они измеряются в угловых единицах. Дело в том, что уклонения отвеса на Земле составляют секунды дуги, поэтому вместо тригонометрических формул, связывающих уклонения отвеса с компонентами вектора силы тяжести, мы взяли простое отношение.

С другой стороны

поэтому

(8.21)

(8.22)

Формула (8.19) позволяет вычислить высоты геоида, если на поверхности Земли заданы смешанные гравитационные аномалии. Принципиально не имеет значения, в каких координатах заданы эти аномалии и в каких координатах практически ведется интегрирование. Мы для этих целей будем применять геодезические координаты и . Перепишем формулу (8.19)

Интегрирование будем выполнять на сфере, а не на эллипсоиде. При этом можно ожидать погрешность в определении высот геоида порядка сжатия. Пренебрегая этими погрешностями, определим элементарные приращения для осей PX и PY

поэтому

(8.23)

Теперь нужно вычислить производные и . Для этого обратимся к формулам сферической тригонометрии.

Рассмотрим сферический треугольник, который образуют дуги, соединяющие три точки на сфере: точку , в которой мы хотим определить уклонение отвеса, точку

-- полюс, и точку -- текущую точку на поверхности сферы, где расположен элемент поверхности. Дуга PN равна 90-, а дуга QN равна 90-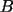. Угол при точке равен

-- азимуту текущей точки Дуга РР' равна аргументу функции Стокса -- . Угол

формулы сферической тригонометрии, несложно получить производные угла по и по , входящие в формулы (8.23)

Подставим полученные выражения в (8.23), получим

Запишем приведенный интеграл в виде двукратного интеграла. Элемент сферы

Эти формулы носят имя голландского ученого Венинг-Мейнеса. Как и в формулу

На практике используют более сложные методики для вычисления уклонений отвеса с использованием и гравиметрических и геодезических данных.

Лекция 9. Квазигеоид Молоденского

•9.1 Критика классической теории Стокса

•9.2 Система высот

•9.3 Краевые условия задачи Молоденского

9.1 Критика классической теории Стокса

Применение формулы Стокса для определения высот геоида относительно общего земного эллипсоида наталкивается на серьезные трудности. Во-первых, для интегрирования необходимо, чтобы гравитационные аномалии были известны по всей поверхности Земли, более двух третей которой покрыта морями и океанами.

Измерение силы тяжести на поверхности океанов стало возможно лишь в ХХ столетии.

В 1922-1929 годы голландский ученый Ф.А.Венинг-Мейнес работал над созданием аппаратуры для измерения силы тяжести на подвижном основании. Наконец, в 1929 году им был создан окончательный вариант маятникового прибора с которым ВенингМейнес совершил плавание на подводной лодке в акваторию юго-восточной Азии, где в то время у Голландии были колонии. Точность гравиметрической съемки ученый оценил в 3-4 мГал, что было достаточно для изучения состояния земной коры в том регионе. На основании этих данных предложил новую теорию изостазии.

Уже в 1930 году заведующий кафедрой гравиметрии механико-математического факультета МГУ профессор Л.В.Сорокин совершил первое плавание в Черном море также на подводной лодке с оригинальной аппаратурой, изготовленной в мастерских ГАИШ. В 1954 году силами института ВНИИГеофизика был создан первый в мире морской гравиметр, а в 1955 году прошел морские испытания на подводной лодке во время плавания вокруг Новой Земли. Результаты убедительно показали, что точность гравиметра не уступает точности маятникового прибора, требует гораздо более простой обработки наблюдений. Маятниковые приборы наземной гравиметрии, как известно, были вытеснены гравиметрами, то же произошло и с морскими приборами. Морские гравиметры сейчас являются основными инструментами морской гравиметрии. Все меньше и меньше остается "белых" пятен на Земле, где сила тяжести неизвестна Вторая проблема -- более серьезная. Теория Стокса требует, чтобы все массы

лежали под уровенной поверхностью, называемой геоидом. Кроме того, измерения силы тяжести выполняются на физической поверхности, не совпадающей с геоидом. Задача состоит в том, чтобы в измеренной значение внести такие поправки, которые бы перенесли все массы под уровень моря, не изменяя самой уровенной поверхности, а сила тяжести оказалась бы отнесенной к уровню моря (геоиду). Эта проблема широко обсуждалась в научной литературе и получила название проблемы регуляризации Земли.

Оказалось, что для успешного решения проблемы регуляризации необходимо знать внутреннее строение Земли. В научный спор о том, как решать проблему регуляризации, в 50-х годах вмешался М.С.Молоденский, который доказал, что