h 
200 км
500 км
1000 км
5000 км
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0.86 |
|
0.68 |
|
0.48 |
|
0.055 |
|
|
|
|
|
|
|
|
|
4 |
|
0.80 |
|
0.59 |
|
0.36 |
|
0.017 |
|
|
|
|
|
|
|
|
|
6 |
|
0.76 |
|
0.51 |
|
0.27 |
|
0.005 |
|
|
|
|
|
|
|
|
|
8 |
|
0.71 |
|
0.44 |
|
0.20 |
|
- |
|
|
|
|
|
|
|
|
|
10 |
|
0.67 |
|
0.37 |
|
0.15 |
|
- |
|
|
|
|
|
||||
20 |
|
0.49 |
|
0.18 |
|
0.035 |
|
- |
|
|
|
|
|
|
|
|
|
50 |
|
0.19 |
|
0.018 |
|
-- |
|
- |
|
|
|
|
|
|
|
|
|
100 |
|
0.041 |
|
-- |
|
-- |
|
- |
|
|
|
|
|
|
|
|
|
Таблица показывает, что для выполнения задачи измерения вторых производных годятся лишь очень низкие спутники. Причем на высоте 200 км от гармоник степени и порядка 100 остается лишь около 4%. Это означает, что если на поверхности Земли нас может удовлетворить точность 1% от амплитуды аномалий градиента, то в космических условиях мы будем вынуждены требовать точность на два порядка выше. Следовательно, в качестве приемлемой точности измерения мы должны планировать чувствительность приборов не менее 0,001Э, что эквивалентно градиенту 
мГал/м 
g/м. Такой высокой чувствительности в земных условиях вряд ли можно достигнуть. Однако в космосе, в условиях глубокого вакуума и сверхнизких температурах надежда на успех остается.
Лекция 8. Определение фигуры геоида
•8.1 Возмущающий потенциал
•8.2 Краевая задача Дирихле для сферы
•8.3 Краевые задачи Неймана
•8.4 Смешанная краевая задача
•8.5 Определение высот геоида
•8.6 Определение уклонений отвеса
8.1 Возмущающий потенциал
Среди специалистов по высей геодезии широко применяется термин возмущающий потенциал, как разность между реальным и нормальным потенциалами в одной
точке. Нельзя сказать, что термин удачен. В небесной механике часто употребляется термин возмущающие силы, возмущающая силовая функция, возмущения. Возникает вопрос, что именно возмущает данная сила? Для небесной механики ответ ясен -- закон движения тела, делает его отличным от кеплеровского, невозмущенного. Правда, терминология московской и петербургской школ небесных механиков различаются. Москвичи говорят функция возмущающая, а петербуржцы -- пертурбационная. Так что же "возмущает" возмущающий потенциал? Ответ -- ничего. По-видимому прав австрийский геодезист Г.Мориц, который предлагает ввести термин аномалия потенциала. Говорим же мы аномалия силы тяжести, имея в виду разность реальной и нормальной силы тяжести! Но отдавая дань традиции, мы будем употреблять термин возмущающий потенциал именно как разность реального и нормального потенциалов тяжести или притяжения взятых в одной и той же точке. Возьмем точку 
на поверхности геоида -- уровенной поверхности -- с координатами
, где |
геодезическая высота точки (расстояние |
от уровенной поверхности |
до эллипсоида) |
Другими словами это высота геоида |
в точке . Две другие |
координаты -- |
и соответственно геодезические широта и долгота (см. лекцию 2, |
|
раздел 2.3). На поверхности эллипсоида точку с такими же значениями широты и
долготы будем обозначать буквой 
. Понятно, что высота этой точки равна нулю. Сила тяжести в точке 
:
Нормальная сила тяжести в точке 
:
Разность абсолютных значений этих векторов определяет смешанную гравитационную аномалию.
Возмущающий потенциал в точке 
(на эллипсоиде) равен
Однако, поскольку 
, получим
(8.1)
Определим смешанную аномалию
(8.2)
В первом слагаемом мы дифференцируем потенциал по внешней нормали к геоиду, а во втором -- к эллипсоиду. Эти два направления, вообще говоря, не совпадают.
Правда, отличие не велико и ошибка составляет всего , то есть величину порядка квадрата отклонения отвесной линии. Это существенно меньше квадрата сжатия, поэтому в нашем приближении можно не делать различия в направлениях отвесной линии и нормали к эллипсоиду.
"Опустим" значение силы тяжести из точки 
в точку 
, применяя формулы линейного приближения
(8.3)
Вертикальный градиент силы тяжести, как мы видели (см. лекцию 7, уравнение (7.12)), зависит от радиусов кривизны нормальных сечений и угловой скорости вращения Земли
(8.4)
Пренебрегая малыми порядка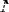 
, можно пренебречь и членом 
. Кроме того, поскольку 
также малая величина (сравнению с 
), можно не учитывать различия между радиусами кривизны меридионального сечения и сечения в первом вертикале. После упрощений, формула (8.3) принимает вид
(8.5)
Теперь смешанную аномалию можно записать так
Разность |
|
есть возмущающий потенциал в точке |
, а тот, в свою |
||
очередь, |
связан с |
высотой |
геоида |
формулой (8.1). Заменяя |
в этой формуле |
реальное |
значение |
силы |
тяжести |
на нормальное, получим |
. Теперь |
смешанную аномалию можно выразить через возмущающий потенциал следующим образом
(8.6)
Итак, задача определения фигуры геоида (поверхности уровня относительно эллипсоида) сводится к определению гармонической функции Т -- возмущающего потенциала, который линейно связан с высотой геоида. Проблема интегрирования уравнения Лапласа, при условии, что на заданной поверхности искомая функция подчиняется некоторому условию, которое называют краевым условием, принадлежит к большому классу краевых задач, с некоторыми из них мы и познакомимся.
8.2 Краевая задача Дирихле для сферы
Попытаемся решить следующую задачу. Дано дифференциальное уравнение
Лапласа, определяющее функцию 
, гармоническую в некоторой области, ограниченной замкнутой поверхностью 
. Все значения этой функции на границе области, то есть на поверхности 
, известны. Из всех решений уравнения Лапласа требуется выбрать только те, которые удовлетворяют краевому условию. Решение этой задачи существенным образом зависит от вида граничной поверхности. Покажем, как она решается, если заданная поверхность -- сфера. В данной формулировке имеем дело с внутренней проблемой Дирихле.
Иногда требуется определить гармоническую функцию вне граничной поверхности.
Тогда это внешняя проблема Дирихле.