22.Моменты инерции площади сечения.

Дадим определения этим геометрическим характеристикам для сечения произвольной формы (рис. 5.1).

Статическим моментом площади относительно некоторой оси называется взятый по всей его площади интеграл от произведения площади элементарного участка dA на расстояние от его центра тяжести до рассматриваемой оси.

(5.1)

Статические моменты выражаются в см³ и м³.

Статический момент площади составной фигуры относительно какой-либо оси равен сумме статических моментов площадей отдельных фигур относительно этой же оси.

Статический момент площади может быть положительным, отрицательным или равным нулю. Он равняется нулю тогда, когда рассматриваемая ось проходит через центр тяжести площади сечения.

Осевым (экваториальным) моментом инерции сечения относительно некоторой оси называется взятый по всей его площади А интеграл от произведения площади элементарного участка dA на квадрат расстояния от его центра тяжести до рассматриваемой оси:

(5.4)

Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятый по всей его площади А интеграл от произведения площади элементарного участка dA на квадрат расстояния от его центра тяжести до рассматриваемой точки (полюса):

(5.5)

Центробежным моментом инерции сечения относительно некоторых двух взаимно перпендикулярных осей называется взятый по всей его площади А интеграл от произведения площади элементарного участка dA на расстояния от его центра тяжести до рассматриваемых осей:

(5.6)

Моменты инерции измеряются в см⁴ и м⁴. Осевые и полярные моменты инерции всегда положительны. Центробежные моменты инерции могут быть положительными, отрицательными или равными нулю.

Центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с его осями симметрии, равен нулю.

23.Зависимость между моментами инерции относительно параллельных осей. Вычисление моментов инерции сложных сечений.

Определим момент инерции фигуры относительно какой-либо оси (рис. 3.4).

Пусть - центральная ось и момент инерцииизвестен. Из чертежа видно. Следовательно

Первый интеграл дает площадь поперечного сечения. Второй интеграл, представляющий статический момент относительно центральной оси равен рулю.

Рис. 3.4. Параллельный перенос осей

Третий интеграл представляет собой момент инерции относительно оси . Таким образом

(3.13)

и относительно ортогональной оси

. (3.14)

Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.

Из формул (4.13) и (3.14) видно, что момент инерции относительно центральной оси меньше, чем момент инерции относительно любой нецентральной оси, которая параллельно центральной.

Момент инерции относительно центральной оси называется центральным моментом инерции.

Положение главных центральных осей и величины главных центральных моментов инерции для симметричных сечений определяются в следующем порядке:

1. Сложное сечение разбивается на простые фигуры (круг, прямоугольник, двутавр, уголок и т.п.) и проводятся их центральные оси Z_i и Y_i (как правило – горизонтально и вертикально).

2. Определяется по формулам (5.3) положение центра тяжести всего сечения и через эту точку проводятся его центральные оси Z и Y. При наличии двух осей симметрии центр тяжести всего сечения находится в точке их пересечения.

Если сечение обладает только одной осью симметрии, то по формулам (5.3) определяется только одна координата центра тяжести. Поясним это для фигуры, показанной на рис. 5.8:

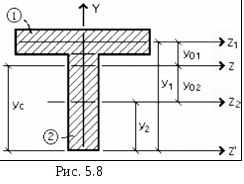
а) оси Z' и Y' выбираем так, чтобы ось Y' совпала с осью симметрии фигуры, а ось Z' – чтобы было удобно определить расстояние до этой оси от центральных осей простых фигур;

б) определяем статический момент площади сечения относительно произвольной оси Z' по формуле:

= А₁у₁ + А₂у₂,

где А_i – площади сечений простых фигур; у_i – расстояния от произвольной оси Z' до центральных осей простых фигур Z_i. Расстояния у_i необходимо брать с учетом знаков;

в) определяем координату у_C центра тяжести по формуле (5.3):

= 

г) на расстоянии у_C от оси Z проводим вторую центральную ось Z. Первой центральной осью является ось симметрии Y.

3. Моменты инерции относительно главных центральных осей Z и Y (рис. 5.8) определяем по формулам (5.9), которые в развернутом виде запишутся так:

так как одна из рассматриваемых осей

(ось Y) является осью симметрии.

В этих формулах:

–осевые моменты инерции простых фигур относительно своих центральных осей (собственные моменты инерции), которые определяются по формулам (5.10)–(5.19) или по таблицам сортаментов для прокатных элементов;

–расстояния от общих центральных осей сечения Z и Y до центральных осей простых фигур. В рассматриваемом примере ипоказаны на рис. 5.8;

A_i – площади простых фигур. Если простой фигурой является фигура, вырезанная от общей, т.е. "пустая" фигура, то в соответствующие формулы площади таких фигур A и их собственные моменты инерции подставляются со знаком "минус".