Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Терёхина, Фикс - Высшая математика

.pdf

Скачиваний:

136

Добавлен:

29.05.2015

Размер:

2.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 219 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

2.4.5. wY^ISLENIE OB_EMOW TEL WRA]ENIQ I PLO]ADEJ POWERHNOSTI WRA]ENIQ tABLICA 2.3.

	b		b
1.a)	Vox = Za	y2(x) dx	2. Vox = aZ [y22(x) ;y12(x)] dx
	8 x = x(t)		t2
1.b)	8 x = x(t)		Vox = y2(t) x0(t) dt
	< y = y(t)		tZ1
	:

d		d
3. Voy = Zc	x2(y) dy	4. Voy = Zc [x22(y) ; x12(y)] dy

	Voy = 2 Zb x y (x) dx	6. FWRox: = 2 Zb y(x)
5.	Voy = 2 Zb x y (x) dx	6. FWRox: = 2 Zb y(x)		1 + yx02	dx:
	a	a	q

oTMETIM, ^TO PRI RE[ENII ZADA^I NEOBHODIMO NARISOWATX FIGURU, SOPOSTAWITX SO SLU^AQMI, UKAZANNYMI W TABLICE 2.3, I PODOBRATX NUVNU@ FORMULU.

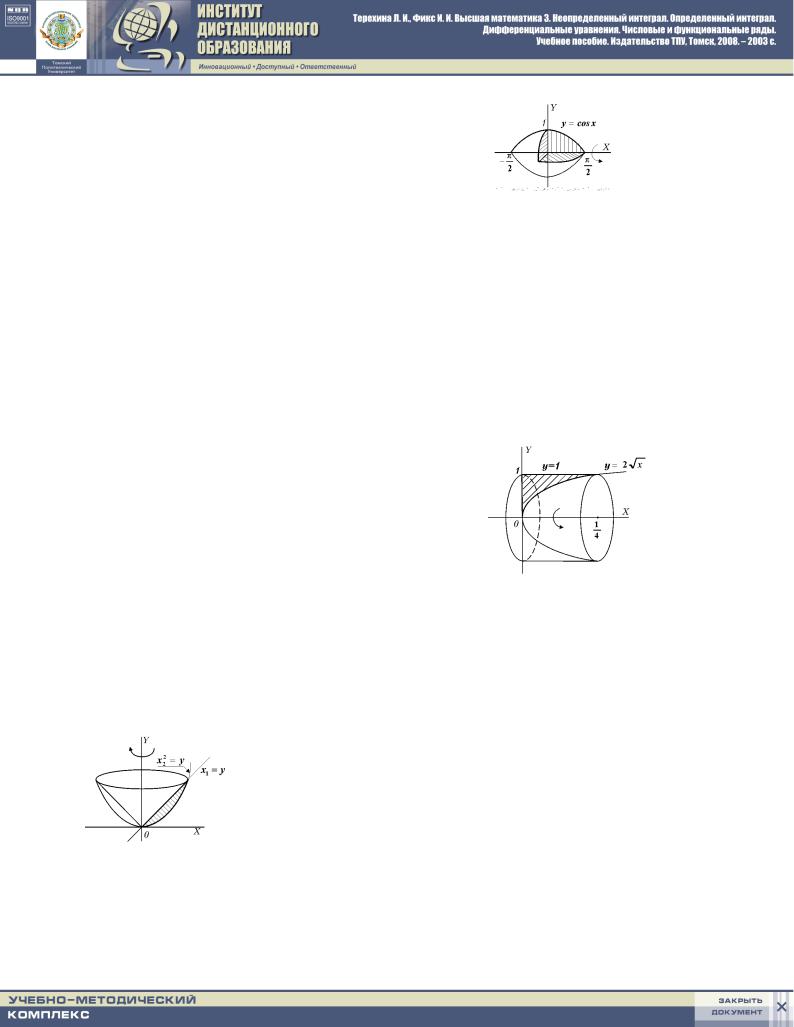
nAJTI OB_EM TELA WRA]ENIQ WOKRUG OSI OX FIGURY,

OGRANI-

^ENNOJ LINIQMI

y = cos x

y = 0:

dELAEM RISUNOK I WIDIM, ^TO DANNYJ SLU-

^AJ SOOTWETSTWUET SLU^A@ 1.a) TABLICY 2.3.

Vox = Z

(x) dx:

iSHODNAQ FORMULA

pREDELY INTEGRIROWANIQ NAHODIM IZ RAWENSTWA

cos x = 0

x1 = ; =2

x2 =

=2:

tOGDA

=2 1 + cos 2x

Vox =

cos2 x dx = 2

cos2 x dx = 2 Z

dx =

; =2

sin 2x

sin

= Z (1 + cos 2x) dx =

x +

2 :

nAJTI OB_EM TELA WRA]ENIQ WOKRUG OSI OX FIGURY,

OGRA-

NI^ENNOJ LINIQMI y = 2px

y = 1

x = 0:

dELAEM RISUNOK I WIDIM,

^TO DANNYJ SLU^AJ

SOOTWETSTWUET SLU^A@ 2 TABLICY 2.3.

pRI-

^EM

y2(x) = 1

y1(x) = 2px:

Vox = Za

[y22(x) ; y12(x)] dx:

pREDELY INTEGRIROWANIQ NAHODIM IZ RAWEN-

STWA

2px = 1

x = 1=4:

tOGDA

1=4

Vox = Z [12 ; (2px)2] dx =

Z (1 ; 4x) dx = (x ; 2x2)

= 8 :

nAJTI OB_EM TELA WRA]ENIQ WOKRUG OSI OY FIGURY, OGRANI-

^ENNOJ LINIQMI

y =

y = x:

dELAEM RISUNOK I WIDIM, ^TO DANNYJ SLU^AJ

SOOTWETSTWUET SLU^A@ 4 TABLICY 2.3.

Voy = Zc [x22(y) ; x12(y)] dy:

pREDELY INTEGRIROWANIQ NAHODIM IZ RAWEN-

STWA

x = x =) x1 = 0 x2 = 1

= c = 0 y2

= d

= 1:

tOGDA, U^ITYWAQ,

x1(y) = y

POLU^IM

^TO x2 (y) = y

(y) = y

Voy = Z (y ; y2) dy =

2 ;

0 =

;

3! =

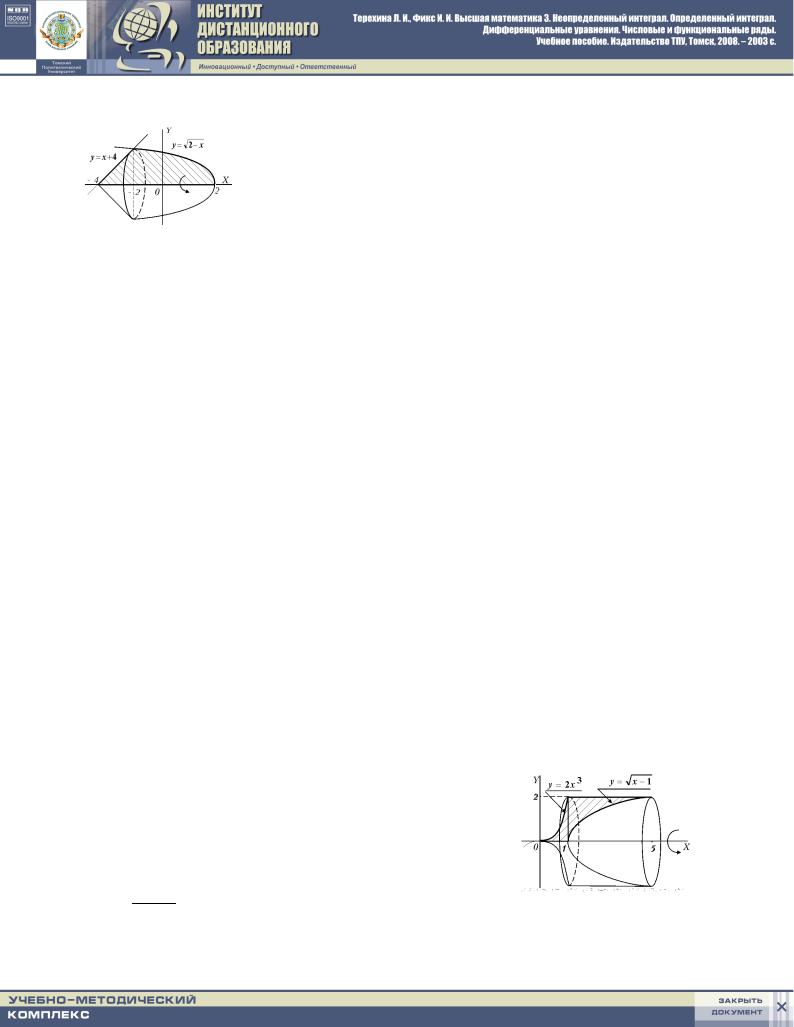
	4. nAJTI OB_EM TELA WRA]ENIQ WOKRUG OSI OX FIGURY, OGRANI-
^ENNOJ LINIQMI y = p2 ; x y = x + 4 y = 0:
	dELAEM RISUNOK I WIDIM, ^TO DANNYJ SLU^AJ SO-
	OTWETSTWUET SLU^A@ 1.a) TABLICY 2, NO S TOJ RAZ-
	NICEJ, ^TO PRI IZMENENII x OT ;4 DO 2 FIGURA
	SWERHU OGRANI^ENA DWUMQ LINIQMI, I OB_EM TELA
	WRA]ENIQ BUDET RAWEN SUMME OB_EMOW.

nAJDEM KOORDINATY TO^KI PERESE^ENIQ PRQMOJ I PARABOLY

x + 4 = p

x2 + 8x + 16 = 2

; x

; x =)

+ 9x + 14 = 0

x1 =

= ;2

(x1

= ;7 -

POSTORONNIJ KORENX

tAKIM OBRAZOM, IMEEM

y(x) = 8 x

+ 4 x

[;4

;2]

< p2

;

[

2 2]:

Vox

= Za

(x) dx

pRI NAHOVDENII OB_EMA PO FORMULE

NEOB

HODIMO RAZBITX INTEGRAL NA DWA INTEGRALA, W KAVDOM IZ KOTORYH

BUDET SWOQ PODYNTEGRALXNAQ FUNKCIQ

Vox = Z (x + 4)2 dx + Z (p2 ; x)2 dx =

Z (x2 + 8x + 16) dx+

2 =

+ Z (2 ; x) dx = ( 3

+ 4x2 + 16x)

;

4 + (2x ;

2 )

;

3 :

nAJTI OB_EM TELA WRA]ENIQ WOKRUG OSI OX FIGURY,

OGRA-

NI^ENNOJ LINIQMI y = 2 x3

y = px ; 1

y = 0

y = 2:

iZ RISUNKA WIDNO, ^TO W DANNOM SLU^AE OB_EM TE- LA WRA]ENIQ TAKVE BUDET RAWEN SUMME OB_EMOW, PERWYJ IZ KOTORYH V1 NAHODITSQ PO FORMULE 1 TABLICY 2.3, A WTOROJ OB_EM V2; PO FORMULE 2. nAJDEM KOORDINATY TO^EK PERESE^ENIQ PRQMOJ I PARABOL

2x3 = 2 =) x = 1 px ; 1 = 2 =) x = 5:

tAKIM OBRAZOM, IMEEM

Vox = V1 + V2 = Z1(2x3)2 dx + Z5

22 ; (p

x ; 1)2

dx =

= Z1

4x6 dx + Z5 (4

; (x ; 1)) dx = Z1

4x6 dx + Z5

(5 ; x) dx =

4x7

+ 05x

25 1

; 2 1

1 =

+ 25 ; 5

; 2 + 2

= 7 :

nAJTI OB_EM TELA WRA]ENIQ WOKRUG OSI OY FIGURY, OGRA-

NI^ENNOJ LINIQMI

x2 + 4y2 = 2

x = 2y

x = 0 (x 0 y 0):

sWERHU FIGURA OGRANI^ENA \LLIPSOM, KANONI^ESKOE URAWNENIE KOTO-
	x2		y2	= 1 POLUOSI a = p		b = 1=p
ROGO		+			2		2
	2		1=2

dELAEM RISUNOK I WIDIM, ^TO DANNYJ SLU^AJ SOOTWETSTWUET SLU^A@ 3 TABLICY 2.3 S TOJ LI[X RAZNICEJ, ^TO INTEGRAL

Voy = Zc

NEOBHODIMO RAZBITX NA DWA

TAK KAK

x (y) dy

y 2 [0

]

x(y) = > p

[

;

tO^KI PERESE^ENIQ \LLIPSA I PRQMOJ

NAHODQTSQ IZ RAWENSTWA

;

= 2y

2 ; 4y

)

= 4y

= 2

y = 1=2:

iTAK, ISKOMYJ OB_EM BUDET SKLADYWATXSQ IZ DWUH OB_EMOW: OB_EMA

V1 OT WRA]ENIQ PRQMOJ	x = 2y	I OB_EMA V2	OT WRA]ENIQ DUGI \L-
LIPSA
1=2	1=p2	1=2	1=p2

Voy = V1+V2 = Z (2y)2 dy+ Z (2;4y2) dy = Z 4y2 dy+ Z (2;4y2) dy =
				0				1=2						0			1=2
4y3					4y3			1=p		1	2			4	1		1
			1=2						2
=	3	j	0	+ 02y	; 3	1	j	1=2		= 0	+ p	;	1	;3	p	3	+ 1	0	86:

				@		A				6	2				( 2)		6
										@							A

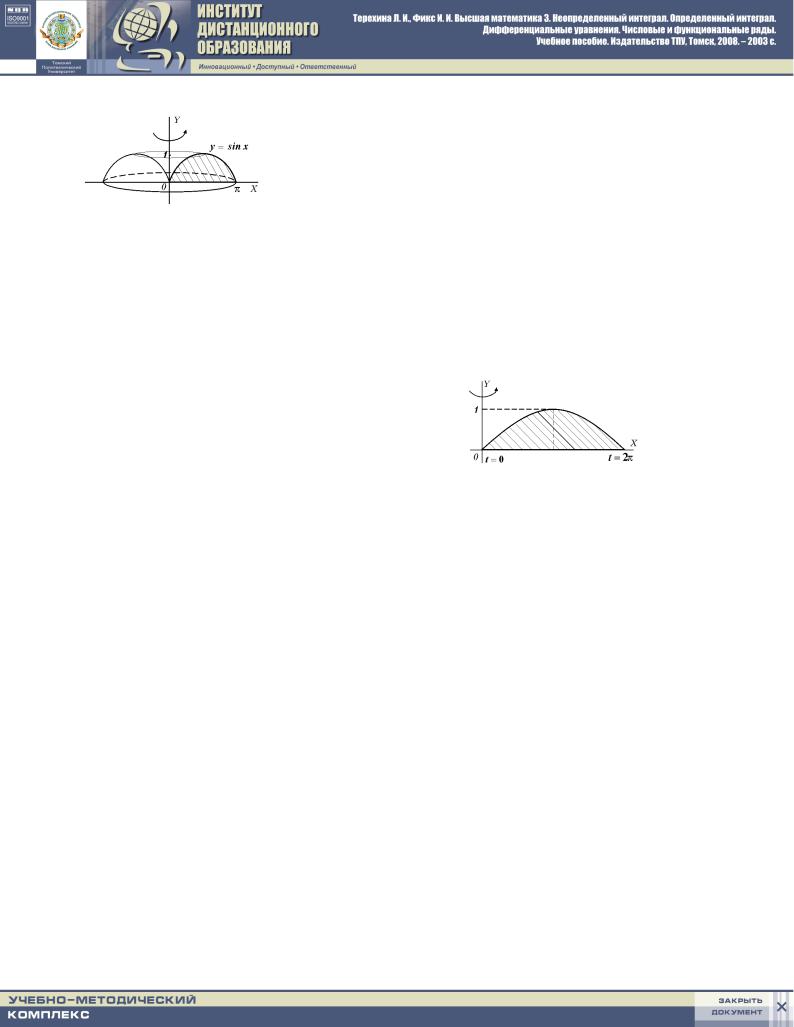
7. nAJTI OB_EM TELA WRA]ENIQ WOKRUG OSI OY FIGURY, OGRANI-
^ENNOJ LINIQMI				y = sin x y = 0 0 x :
				pRI NAHOVDENII OB_EMA TELA WRA]ENIQ PO
					d
				FORMULE Voy = Zc		x2(y) dy NAM POTREBUETSQ
RE[ATX INTEGRAL				R arcsin2 y dy	^TO QWLQETSQ DOWOLXNO TRUDOEMKOJ
ZADA^EJ, PO\TOMU WOSPOLXZUEMSQ FORMULOJ 5, TABLICA 2.3
	b
Voy = 2 Za		x y(x) dx = 2 Z x			sin x dx =	j iNTEGRIRUQ PO ^ASTQM
POLU^IM j			;x	0		cos( ) = ; (;1) = :
		=		cos x j0 + sin x j0 = ;
8. nAJTI OB_EM TELA WRA]ENIQ WOKRUG OSI OY FIGURY, OGRANI-
^ENNOJ CIKLOIDOJ
8 x = t	; sin t		I OSX@ OX :		y = 0:
< y = 1	; cos t
:

zDESX TAKVE UDOBNEE ISPOLXZOWATX FORMULU 5 DLQ WY^ISLENIQ OB_EMA

Voy = 2 aZ

x y(x) dx

W KOTOROJ DELAEM ZAMENU PEREMENNOJ

dx = x0

x = t

;

sin t

y = 1

;

cos t

= (1

;

cos t) dt

pRIRAWNIWAQ

y = 1 ; cos t

I y = 0 NAHODIM PREDELY INTEGRI-

ROWANIQ

t1 = 0 t2

= 2 :

tOGDA

Voy

= 2 Z (t ; sin t) (1 ; cos t) (1 ; cos t) dt =

= 2 Z

(t;sin t) (1;cos t)2 dt = 2 Z (t;sin t) (1;2 cos t+cos2 t) dt =

= 2 Z

(t ; sin t ; 2t cos t + 2 sin t cos t + t cos2 t ; sin t cos2 t) dt =

t cos 2t

= 2 Z (t ;sin t ;2t cos t + 2 sin t cos t +

;sin t cos2 t) dt =

= 2 Z (t +

) dt = 2 2

= 6 3:

2 0

iNTEGRALY OTOSTALXNYH SLAGAEMYH BUDUT RAWNY NUL@.

2.4.7. nEBERU]IESQ INTEGRALY

nARQDU S RASSMOTRENNYMI KLASSAMI INTEGRIRUEMYH FUNKCIJ SU- ]ESTWUET BOLX[OJ KLASS NEINTEGRIRUEMYH FUNKCIJ, T.E. FUNKCIJ, INTEGRALY OT KOTORYH NE WYRAVA@TSQ W \LEMENTARNYH FUNKCIQH.

nAPRIMER, K NEBERU]IMSQ OTNOSQTSQ INTEGRALY

ex2 dx

cos(x2) dx

sin(x2) dx

sin x

ln x

cos x

Z arctg2x dx

Z xtg x dx

A TAKVE SLU^AI NEINTEGRIRUEMOSTI DIFFERENCIALXNYH BINOMOW I DR.

oDNAKO, ESLI INTEGRALY OT TAKIH FUNKCIJ QWLQ@TSQ OPREDELENNY- MI, A TAKVE, ESLI NAHOVDENIE PERWOOBRAZNOJ QWLQETSQ O^ENX TRU- DOEMKOJ ZADA^EJ, PRIBEGA@T K PRIBLIVENNYM METODAM WY^ISLENIQ OPREDELENNYH INTEGRALOW, SREDI KOTORYH NAIBOLEE TO^NYM QWLQETSQ METOD sIMPSONA, KOTORYJ LEGKO REALIZOWATX NA |wm.

			b
pRIBLIVENNOE RAWENSTWO			Za	f(x) dx
b ; a		[ y0 + y2n + 2(y2		+ : : : + y2n	;	2) + 4(y1 + : : : + y2n	;	1) ]
6n					;		;
NAZYWAETSQ	FORMULOJ PARABOL ILI FORMULOJ sIMPSONA.

sOGLASNO \TOJ FORMULE PROMEVUTOK INTEGRIROWANIQ DELITSQ NA ^ET- NOE ^ISLO ^ASTEJ 2n I WY^ISLQ@TSQ ZNA^ENIQ PODYNTEGRALXNOJ FUNKCII WO WSEH TO^KAH

x0 x1 x2 : : : x2n;2 x2n;1 x2n: pOLU^ENNYE ZNA^ENIQ FUNKCII

y(x0) = y0 y(x1) = y1 y(x2) = y2 : : :

: : : y(x2n;2) = y2n;2 y(x2n;1) = y2n;1 y(x2n) = y2n

PODSTAWLQ@TSQ W FORMULU, W KOTOROJ, KAK LEGKO ZAMETITX, SGRUP- PIROWANY ZNA^ENIQ S NE^ETNYMI I ^ETNYMI NOMERAMI. mETOD LEGKO REALIZOWATX DAVE WRU^NU@, WZQW NE O^ENX BOLX[IE ZNA^ENIQ 2n OD- NAKO TO^NOSTX METODA WOZRASTAET PRI UWELI^ENII ^ISLA RAZBIENIJ PROMEVUTKA. pO\TOMU DLQ DOSTIVENIQ BOLX[OJ STEPENI TO^NOSTI ISPOLXZUETSQ |wm.

g L A W A 3. differencialxnye urawneniq i sistemy

dIFFERENCIALXNOE URAWNENIE QWLQETSQ ODNIM IZ WAVNEJ[IH MATE- MATI^ESKIH PONQTIJ.

dIFFERENCIALXNOE URAWNENIE { \TO URAWNENIE, KOTOROE SWQZYWAET NEZAWISIMYE PEREMENNYE, ISKOMU@ FUNKCI@ I PROIZWODNYE ISKOMOJ FUNKCII PO NEZAWISIMYM PEREMENNYM.

dIFFERENCIALXNOE URAWNENIE DLQ OTYSKANIQ FUNKCII ODNOJ NE- ZAWISIMOJ PEREMENNOJ NAZYWAETSQ O B Y K N O W E N N Y M. eSLI ISKOMAQ FUNKCIQ ZAWISIT OT NESKOLXKIH PEREMENNYH, TO GOWORQT O DIFFERENCIALXNOM URAWNENII W ^ASTNYH PROIZWODNYH. w DANNOM PO- SOBII MY BUDEM RASSMATRIWATX TOLXKO OBYKNOWENNYE URAWNENIQ. p O R Q D O K DIFFERENCIALXNOGO URAWNENIQ OPREDELQETSQ PORQDKOM STAR[EJ PROIZWODNOJ, WHODQ]EJ W URAWNENIE.

nAHOVDENIE RE[ENIQ DIFFERENCIALXNOGO URAWNENIQ NAZYWAETSQ EGO INTEGRIROWANIEM, POTOMU ^TO W BOLX[INSTWE SLU^AEW \TO DEJST- WITELXNO INTEGRIROWANIE. mETOD RE[ENIQ URAWNENIQ OPREDELQETSQ TIPOM URAWNENIQ. dALEKO NE WSQKOE URAWNENIE DOPUSKAET ANALITI^ES- KOE RE[ENIE, I TOGDA DLQ POLU^ENIQ RE[ENIQ PRIHODITSQ PRIBEGATX K ^ISLENNYM METODAM.

dIFFERENCIALXNOE URAWNENIE, POLU^ENNOE W REZULXTATE ISSLEDO- WANIQ KAKOGO-LIBO REALXNOGO PROCESSA ILI QWLENIQ, NAZYWA@T DIF- FERENCIALXNOJ MODELX@ \TOGO PROCESSA ILI QWLENIQ. w PROCESSE PO- STROENIQ DIFFERENCIALXNYH MODELEJ WAVNOE ZNA^ENIE IMEET ZNANIE ZAKONOW TOJ OBLASTI NAUKI, S KOTOROJ SWQZANA RE[AEMAQ ZADA^A. tA- KIE, NAPRIMER, KAK ZAKONY nX@TONA, oMA, kEPLERA, kIRHGOFA, DEJ- STWIQ MASS, SOHRANENIQ \NERGII, WSEMIRNOGO TQGOTENIQ I T.D.

1. dIFFERENCIALXNYE URAWNENIQ 1-GO PORQDKA

1.1.oSNOWNYE PONQTIQ I OPREDELENIQ

1.dIFFERENCIALXNYM URAWNENIEM 1-GO PORQDKA NAZYWAETSQ URAW- NENIE, SWQZYWA@]EE NEZAWISIMU@ PEREMENNU@, ISKOMU@ FUNKCI@ I EE PERWU@ PROIZWODNU@.

y0 = f(x y)

dIFFERENCIALXNOE URAWNENIE 1-GO PORQDKA MOVET BYTX ZADANO W

TREH FORMAH:
y0 = f(x y) ; QWNAQ,	F (x y y0) = 0 ; NEQWNAQ,

M(x y) dx + N(x y) dy = 0 ; DIFFERENCIALXNAQ.

pRAKTI^ESKI DOSTATO^NO PROSTO PEREHODITX OT ODNOJ FORMY ZAPISI URAWNENIQ K DRUGOJ, I SAMA FORMA ZAPISI URAWNENIQ SOWER[ENNO NE

OPREDELQET TIP URAWNENIQ I METOD EGO INTEGRIROWANIQ. nAPRIMER: (x2 ;y2)y0;2xy+1 = 0 ; NEQWNAQ FORMA, =) y0 = 2xxy2 ;;y12 ; QWNAQ,

)(x2 ; y2)dy ; (2xy ; 1)dx = 0 ; DIFFERENCIALXNAQ FORMA.

2.r E [ E N I E M DIFFERENCIALXNOGO URAWNENIQ NAZYWAETSQ L@- BAQ DIFFERENCIRUEMAQ FUNKCIQ y = y(x) KOTORAQ PRI PODSTANOW- KE W URAWNENIE OBRA]AET EGO W TOVDESTWO. iNTEGRALOM URAWNENIQ NAZYWAETSQ EGO RE[ENIE, POLU^ENNOE W NEQWNOM WIDE.

lEGKO POKAZATX, ^TO KAVDOE DIFFERENCIALXNOE URAWNENIE PERWOGO PORQDKA IMEET BESKONE^NOE MNOVESTWO RE[ENIJ. wSE \TO MNOVESTWO MOVNO OPISATX ODNOJ FUNKCIEJ, KOTORAQ NAZYWAETSQ OB]IM RE[ENI- EM ILI OB]IM INTEGRALOM DIFFERENCIALXNOGO URAWNENIQ. iZ \TOGO MNOVESTWA MOVNO WYBRATX KONKRETNOE (^ASTNOE) RE[ENIE, ESLI ZA- DATX NA^ALXNOE USLOWIE.

3.n A ^ A L X N Y M U S L O W I E M DLQ URAWNENIQ PERWOGO PORQDKA QWLQETSQ ZADANIE ZNA^ENIQ ISKOMOJ FUNKCII PRI ZADANNOM

ZNA^ENII NEZAWISIMOJ PEREMENNOJ, T.E. y(x0) = y0:

4. o B ] I M RE[ENIEM DIFFERENCIALXNOGO URAWNENIQ 1-GO PO- RQDKA NAZYWAETSQ FUNKCIQ y = y(x C) KOTORAQ UDOWLETWORQET SLEDU@]IM USLOWIQM:

a)FUNKCIQ SODERVIT ODNU PROIZWOLXNU@ POSTOQNNU@ C

b)\TA FUNKCIQ QWLQETSQ RE[ENIEM URAWNENIQ PRI L@BYH ZNA^E- NIQH PROIZWOLXNOJ POSTOQNNOJ

c)PRI ZADANNOM NA^ALXNOM USLOWII PROIZWOLXNU@ POSTOQNNU@ MOVNO OPREDELITX EDINSTWENNYM OBRAZOM TAK, ^TO POLU^ENNOE ^ASTNOE RE[ENIE BUDET UDOWLETWORQTX ZADANNOMU NA^ALXNOMU USLO-

WI@.

5. z A D A ^ A k O [ I { NAHOVDENIE ^ASTNOGO RE[ENIQ, UDOW- LETWORQ@]EGO ZADANNOMU NA^ALXNOMU USLOWI@.

f(x y)

6. tEOREMA kO[I. (tEOREMA SU]ESTWOWANIQ I EDINSTWENNOSTI ^ASTNOGO RE[ENIQ DIFFERENCIALXNOGO URAWNENIQ 1-GO PORQDKA.) eS-

LI W URAWNENII y0 = f(x y) FUNKCIQ NEPRERYWNA WMESTE SO SWOEJ ^ASTNOJ PROIZWODNOJ PO y W TO^KE M0(x0 y0) I EE OKREST- NOSTI, TO URAWNENIE IMEET I PRI TOM EDINSTWENNOE ^ASTNOE RE- [ENIE, UDOWLETWORQ@]EE ZADANNOMU NA^ALXNOMU USLOWI@ y(x0) = y0:

7. g E O M E T R I ^ E S K I J S M Y S L DIFFERENCIALXNOGO URAWNENIQ I EGO OB]EGO I ^ASTNOGO RE[ENIJ.

a)gRAFIK y = y(x) RE[ENIQ DIFFERENCIALXNOGO URAWNENIQ y0 = f(x y) NAZYWAETSQ INTEGRALXNOJ KRIWOJ.

b)oB]EE RE[ENIE y = y(x C) URAWNENIQ ESTX SEMEJSTWO INTEG- RALXNYH KRIWYH.

c)dIFFERENCIALXNOE URAWNENIE 1-GO PORQDKA y0 = f(x y) ZADAET SWQZX MEVDU KOORDINATAMI TO^KI M(x y) PLOSKOSTI XOY S UGLOWYM KO\FFICIENTOM KASATELXNOJ K INTEGRALXNOJ KRIWOJ, PROHODQ]EJ ^E- REZ \TU TO^KU.

d)zADANIE NA^ALXNOGO USLOWIQ y(x0) = y0 OZNA^AET ZADANIE TO^KI

NA PLOSKOSTI M0(x0 y0): e) rE[ITX ZADA^U kO[I

y0 = f(x y) y(x0) = y0

OZNA^AET, ^TO IZ WSEGO MNOVESTWA INTEGRALX-

NYH KRIWYH, PREDSTAWLQ@]IH OB]EE RE[ENIE

URAWNENIQ, NEOBHODIMO OTOBRATX TU EDINSTWEN-

NU@, KOTORAQ PROHODIT ^EREZ DANNU@ TO^KU

M0(x0 y0):

f) wYPOLNENIE USLOWIJ TEOREMY kO[I W TO^KE OZNA^AET, ^TO ^E- REZ DANNU@ TO^KU PLOSKOSTI OBQZATELXNO PROHODIT I PRITOM TOLXKO ODNA INTEGRALXNAQ KRIWAQ.

tO^KI (x y) PLOSKOSTI, W KOTORYH NE WYPOLNQ@TSQ USLOWIQ TEO- REMY kO[I, NAZYWA@TSQ O S O B Y M I TO^KAMI. w \TIH TO^KAH TERPIT RAZRYW ILI FUNKCIQ f(x y) ILI EE PROIZWODNAQ fy0 (x y): ~E- REZ KAVDU@ IZ TAKIH TO^EK LIBO PROHODIT MNOVESTWO INTEGRALXNYH KRIWYH, LIBO NE PROHODIT NI ODNOJ.

1.2. oSNOWNYE TIPY URAWNENIJ 1-GO PORQDKA

rASSMOTRIM NEKOTORYE TIPY DIFFERENCIALXNYH URAWNENIJ 1-GO PORQDKA, RE[ENIE KOTORYH, W KONE^NOM ITOGE, SWODITSQ K INTEGRIROWANI@ (RE[ENIE MOVNO PREDSTAWITX W ANALITI^ESKOM WIDE).

pROSTEJ[IMI DIFFERENCIALXNYMI URAWNENIQMI 1-GO PORQDKA QW-


LQ@TSQ URAWNENIQ WIDA	f(x) dx + g(y) dy = 0 HARAKTERNOJ OSO-
BENNOSTX@ KOTORYH QWLQETSQ TO, ^TO MNOVITELEM PRI			dx	QWLQETSQ
FUNKCIQ, ZAWISQ]AQ TOLXKO OT x		A MNOVITELEM PRI	dy	QWLQETSQ
FUNKCIQ, ZAWISQ]AQ TOLXKO OT y:		gOWORQT, ^TO W TAKOM URAWNENII
PEREMENNYE RAZDELENY,	A SAMO URAWNENIE NAZYWAETSQ URAWNENIEM S

RAZDELENNYMI PEREMENNYMI.

rE[ENIE TAKIH URAWNENIJ ZAKL@^AETSQ W PO^LENNOM INTEGRIROWANII
LEWOJ I PRAWOJ EGO ^ASTEJ	Z f(x) dx + Z g(y) dy = C:

pOSLE NAHOVDENIQ INTEGRALOW MY POLU^AEM OB]IJ INTEGRAL URAW- NENIQ F(x y C) = 0: eSLI UDAETSQ WYRAZITX QWNO FUNKCI@ ^EREZ

NEZAWISIMU@ PEREMENNU@ (^TO DALEKO NE WSEGDA WOZMOVNO), TO POLU-
^AEM OB]EE RE[ENIE URAWNENIQ y = f(x C). rASSMOTRIM PRIMER
	cos x dx = p		dy:
		y
dANNOE URAWNENIE QWLQETSQ URAWNENIEM S RAZDELENNYMI PEREMENNY-

MI, TAK KAK PRI dx STOIT FUNKCIQ, ZAWISQ]AQ TOLXKO OT x A PRI dy


STOIT FUNKCIQ, ZAWISQ]AQ TOLXKO OT y: mOVNO INTEGRIROWATX OBE
^ASTI URAWNENIQ R cos x dx = R p				dy:
^ASTI URAWNENIQ R cos x dx = R p			y	dy:
2	3=2	=)			3	2=3
sin x + C = 3 y		=)		y = [	2(sin x + C)]		:
mETODY RE[ENIQ RASSMATRIWAEMYH NIVE URAWNENIJ (KROME URAWNENIJ W POLNYH DIF-
FERENCIALAH) PREDSTAWLQ@T SOBOJ SPOSOBY SWEDENIQ \TIH URAWNENIJ K URAWNENIQM S

RAZDELENNYMI PEREMENNYMI.


1.2.1.	uRAWNENIQ WIDA		y0 = f(x) g(y) ;
	URAWNENIQ S RAZDELQ@]IMISQ PEREMENNYMI
o P R E D E L E N I E.		dIFFERENCIALXNOE URAWNENIE y0 = f(x y) QW-

LQETSQ URAWNENIEM S RAZDELQ@]IMISQ PEREMENNYMI, ESLI EGO PRA- WAQ ^ASTX PREDSTAWLQET SOBOJ, ILI MOVET BYTX PREDSTAWLENA W WIDE PROIZWEDENIQ (ILI OTNO[ENIQ) DWUH FUNKCIJ, ODNA IZ KOTORYH

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 219 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.12.2018280.58 Кб1Теория организации для ТПУ.doc
#
29.05.2015516.61 Кб25Теория экзамен.doc
#
02.05.2019210.94 Кб6теория_«SWOT» анализ_сам.работа.doc
#
12.11.201975.69 Mб0Теория_БЖД_практика.doc
#
30.07.2019118.89 Кб2ТерВер_шпора.docx
#
29.05.20152.54 Mб136Терёхина, Фикс - Высшая математика.pdf
#
22.11.20191.87 Mб7Терминология.doc
#
29.05.201537.45 Кб27Термодин 1-10.docx
#
29.05.201513.16 Кб24Термодин 21-30.docx
#
29.05.201523.55 Кб19Термодин 31-40.doc
#
29.05.2015194.56 Кб17Термодин 71-80.doc