Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Терёхина, Фикс - Высшая математика

.pdf

Скачиваний:

136

Добавлен:

29.05.2015

Размер:

2.54 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2121

4.2. rQD fURXE DLQ PERIODI^ESKOJ S PERIODOM T = 2l FUNKCII, ZADANNOJ NA INTERWALE [;l l]

eSLI FUNKCIQ y = f(x) ZADANA NA INTERWALE [;l l] GDE l{ PROIZWOLXNOE ^ISLO, IMEET PERIOD T = 2l I UDOWLETWORQET NA RAS- SMATRIWAEMOM INTERWALE USLOWIQM TEOREMY dIRIHLE, TO UKAZANNAQ FUNKCIQ MOVET BYTX PREDSTAWLENA W WIDE SUMMY RQDA fURXE

n x

f(x) =

cos

+ bn

sin

(2)

n=1

KO\FFICIENTY

bn NAHODQTSQ PO FORMULAM

1 l

n x

1 l

n x

a0 = l Z f(x) dx

an = l Z

f(x) cos

bn = l Z

f(x) sin

dx:

4.3. rQDY fURXE ^ETNOJ I NE^ETNOJ FUNKCIJ

w SLU^AE, ESLI FUNKCIQ

y = f(x)

QWLQETSQ ^ETNOJ ILI NE^ET-

NOJ, RQD fURXE DANNOJ FUNKCII BOLEE PROST. tAK, RQD fURXE ^ETNOJ FUNKCII SODERVIT TOLXKO SWOBODNYJ ^LEN I ^LENY S KOSINUSAMI. w TAKIH SLU^AQH GOWORQT O RAZLOVENII PO KOSINUSAM, A RQD NE^ETNOJ FUNKCII SODERVIT TOLXKO ^LENY S SINUSAMI I GOWORQT O RAZLOVENII W RQD fURXE PO SINUSAM.

dLQ ^ETNOJ PERIODI^ESKOJ FUNKCII WSE KO\FFICIENTY bn = 0, I RQD fURXE BUDET RQDOM PO KOSINUSAM

n x

f(x) =

an cos nx

f(x) =

an cos

n=1

a0 =

Z f(x) dx

a0 =

f(x) dx

n x

an =

f(x) cos nx dx:

an = l

Z f(x) cos

dx:

dLQ NE^ETNOJ PERIODI^ESKOJ FUNKCII KO\FFICIENTY a0 = 0 an = 0 I RQD fURXE BUDET RQDOM PO SINUSAM

f(x) = X1 bn sin nx

n=1

bn = 2 Z f(x) sin nx dx:

f(x) =

2 bn = l

X
1 bn sin n x
n=1	l

Zl	f(x) sin nl x dx:
0

194

4.4. rQD fURXE NEPERIODI^ESKIH FUNKCIJ

eSLI FUNKCIQ f(x) NEPERIODI^ESKAQ I ZADANA NA PROIZWOLXNOM INTERWALE (a b) TO POD RAZLOVENIEM FUNKCII W RQD fURXE W \TOM PROMEVUTKE PONIMA@T RAZLOVENIE W RQD fURXE PERIODI^ESKOJ FUNK- CII S PERIODOM 2l = b ; a KOTORAQ NA PROMEVUTKE (a b) SOWPADAET S DANNOJ FUNKCIEJ f(x):

~ASTO PODOBNAQ ZADA^A MOVET BYTX SFORMULIROWANA TAK: rAZLOVITX W RQD fURXE FUNKCI@ f(x) NA PROMEVUTKE [0 l] (ILI,

W ^ASTNOSTI, [0 ]) W RQD PO KOSINUSAM ILI PO SINUSAM.

w \TIH SLU^AQH SMYSL ZADA^I ZAKL@^AETSQ W TOM, ^TO RASKLADYWA- ETSQ W RQD SOOTWETSTWENNO ^ETNAQ ILI NE^ETNAQ PERIODI^ESKAQ FUNK- CIQ S PERIODOM T = 2l (ILI T = 2 ), KOTORAQ NA INTERWALE [0 l] (ILI [0 ]) SOWPADAET S ZADANNOJ FUNKCIEJ.

tO ESTX FUNKCI@ DOOPREDELQ@T NA INTERWALE [;l 0] (ILI [; 0]) ^<TNYM ILI NE^<TNYM OBRAZOM I DLQ POLU^ENIQ E< RQDA fURXE IS- POLXZU@T PRIWEDENNYE WY[E FORMULY.

1: rAZLOVITX W RQD fURXE FUNKCI@, ZADANNU@ W INTERWALE (; )
WYRAVENIEM
f(x) = 8x ; 1	; < x < 0
< x + 1	0 < x <
:

tAK KAK DANNAQ FUNKCIQ QWLQETSQ NE^ETNOJ, TO MOVNO ZARANEE SKA-

ZATX, ^TO WSE KO\FFICIENTY an = 0

(n = 0 1 2 3 : : :):

nAHODIM

bn = 2 Z f(x) sin nx dx = 2

Z (x + 1) sin nx dx =

U = x + 1

dV = sin nx dx

= 2

2;x +n

cos nx dx3=

1cos nx + n1

dU = dx

V =

cos nx

+ 1

cos nx

sin nx

0 # =

cos n + n

+0# =

[1 ; ( + 1)

(;1)

= n [1 ; ( + 1) cos n ] = n

] :

195

rQD fURXE DLQ DANNOJ FUNKCII

f(x) = 1 bn sin nx =

2 1

1 ; ( + 1) (;1)n

sin nx:

n=1

zAPI[EM NESKOLXKO PERWYH KO\FFICIENTOW

b1 =

(2 + ) 3 27

b2 =

(; ) = ;1 b3

(2 + ) 1 09

b4 =

(; ) = ;0 5

b5 =

(2 + ) 0 65

b6 = 0 333 : : :

tOGDA RQD fURXE

f(x) = 3 27 sin x;sin 2x+1 09 sin 3x;0 5 sin 4x+0 65 sin 5x;: : :

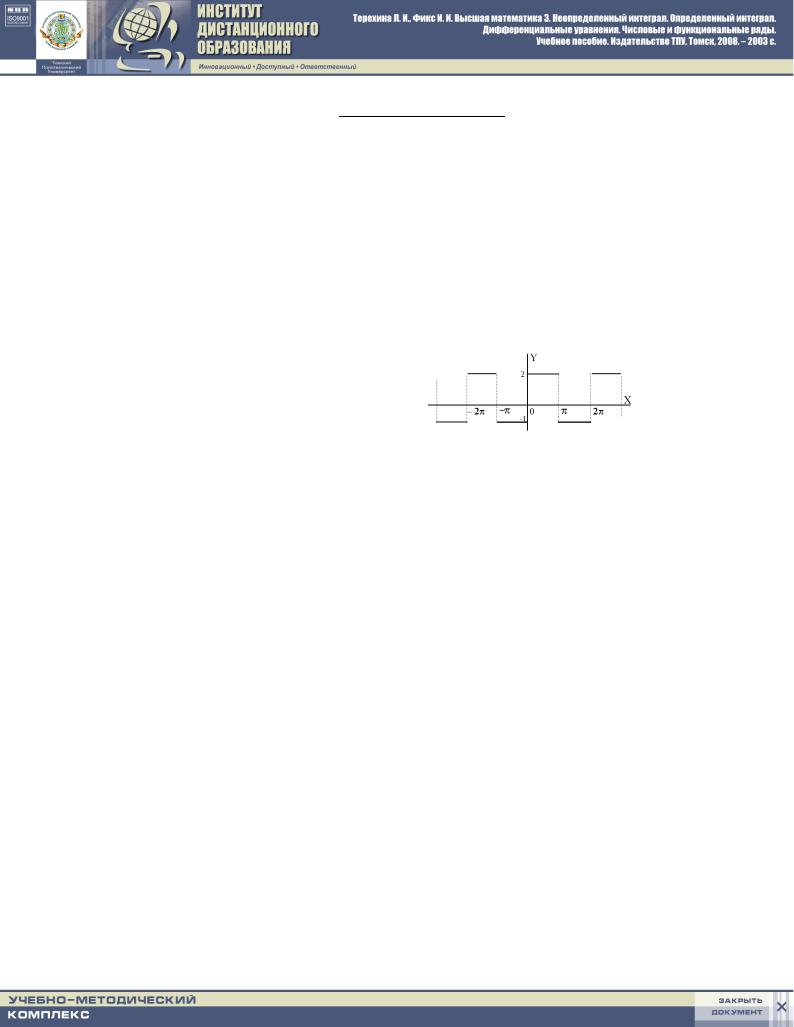
2: rAZLOVITX W RQD fURXE FUNKCI@, ZADANNU@ W INTERWALE (; ) WYRAVENIEM

f(x) = 8;1		; < x < 0
<	2	0 < x <
:

nAJDEM KO\FFICIENTY RQDA fURXE PO SOOTWETSTWU@]IM FORMULAM, U^ITYWAQ ZADANIE FUNKCII NA KAVDOJ ^ASTI INTERWALA

a0 = 1

f(x) dx = j

INTEGRAL RAZBIWAEM NA SUMMU INTEGRALOW j =

;

(

1) dx +

(2) dx

+2 ] = 1:

= 1

x + (2x)

1 [

;

an = 1

f(x) cos nx dx = 1

2 Z

(;1) cos nx dx + Z (2) cos nx dx

3 =

= 1 2;;n1 sin nx

0 + n2

sin nx4;0

3 = 0

T.K. sin n = sin 0 = 0

;

bn = Z

f(x) sin nx dx = ;

(;1) sin nx dx+Z (2) sin nx dx 3=

;

= 1 2 n1 cos nx

;n2 cos nx

[(cos 0;cos n );2(cos n ;cos 0)] =

[;3 cos 0 ;

3 cos5 n ] =

(1 ; cos n ) =

[1 ; (;1)n]:

zDESX MY ZAMENILI cos n = (;1)n:

dALEE, T.K. PRI

n = 2k WY-

RAVENIE [1 ; (;1)2k] = 1 ; 1 = 0

TO WSE KO\FFICIENTY S ^ETNYMI

b2k = 0

n = 2k

; 1

NOMERAMI OBRATQTSQ W NOLX

A PRI

WYRAVENIE

[1;(;1) ; ] = 1+1 = 2 I WSE KO\FFICIENTY S NE^ETNYMI NOMERAMI

196

b2k;1 =

b1 =

1 91 b3

0 64 b5 =

0 38:

(2k 1)

s U^ETOM;NAJDENNYH KO\FFICIENTOW RQD fURXE DLQ DANNOJ FUNKCII

a0 1

1 sin(2k 1)x

f(x) =

2 +

bn sin nx = 2

;

BUDET IMETX WID

n=1

k=1

= 0 5 + 1 91 sin x + 0 64 sin 3x + 0 38 sin 5x + :::

3: rAZLOVITX W RQD fURXE FUNKCI@, ZADANNU@ W INTERWALE (;2 2) WYRAVENIEM

f(x) = 81

;2 < x < 0

< x

0 < x < 2

nAJDEM KO\FFICIENTY RQDA fURXE PO FORMULAM, SOOTWETSTWU@]IM

SLU^A@ PROIZWOLXNOGO l

U^ITYWAQ, ^TO W NA[EM SLU^AE l

= 2

TAKVE ZADANIE FUNKCII NA KAVDOJ ^ASTI INTERWALA.

x2 0

2Z 1 dx + Z x dx3 =

3 =

a0 = 2

;

[ 2 + 2 ] = 2

6;2

;

n x

an =

f(x) cos

dx= 22

1 cos

dx+

x cos

dx3=

;

U = x

dU = dx 5

wTOROJ INTEGRAL BEREM PO ^ASTQM:

dV = cos n x dx V =

sin n x

n x 0

n x 2

sin

+ x

sin

0 ;

cos

3 =

;

n2 2

(sin 0 + sin n ) +

sin n ;

(cos n ; 1)

n2 2

(1 ; cos n ) =

[1 ; (;1)n]:

n2 2

w ITOGE POLU^AEM, ^TO a2k = 0

a2k

1 =

;

(2k ;

3 =

n x

bn = 2

f(x) sin

dx = 2

sin

dx +

sin

;

n x 0

n x 2

3 =

;

cos

2 ; n cos

sin

n2 2

;

2";

(1;cos n );

cos n +0#= ;

(1+cos n ) = ;

[1+(;1)

197

w ITOGE POLU^AEM, ^TO b2k = ;

b2k;1 = 0:

zAPI[EM NESKOLXKO PERWYH KO\FFICIENTOW RQDA fURXE

a0 = 2

a1 =

0 4

a2 = 0

a3 =

0 05

a4 = 0 : : :

9 2

b1 = 0

b2 = ;

0 32

b3 = 0

b4 =

;

0 16 : : :

oKON^ATELXNO

IMEEM RQD fURXE

f(x) = 2

an cos nx+bn sin nx =

n=1

cos(2k

1)x

sin 2kx

= 1 +

;1)2

;

k=1

(2k

k=1

;

= 1 + 0 4 cos x ; 0 32 sin 2x + 0 05 cos 3x ; 0 16 sin 4x + : : :

4: rAZLOVITX FUNKCI@, ZADANNU@ W INTERWALE (0

) WYRAVE-

NIEM

f(x) = ; x

W RQD fURXE PO KOSINUSAM

pREDPOLAGAQ PRODOLVENIE FUNKCII NA

PROMEVUTOK

(; 0)

^ETNYM

OBRAZOM,

IMEEM, ^TO WSE KO\FFICIENTY

bn = 0

A KO\FFICIENTY a0

NAHODQTSQ PO FORMULAM,

SOOTWETSTWU@]IM

SLU^A@ ^ETNOJ FUNKCII W INTERWALE (

a0 = 2 Z f(x) dx = 2

Z (

; x) dx = 2 0;x ; x22 1 j0 = :

;x dV = cos nx dx

an= Z f(x) cos nx dx=

Z( ;x) cos nx dx= V =1 sin nx dU = dx

;

= 2(

+ 1

sin nx

cos nx

sin nx dx) =

sin nx

j0 ;n2

= 2

;

cos n +

! =

(1 ; cos n ) =

[1 ; (;1)n]:

iTAK

POLU^ILI

: a0 =

14 a2k;1 =

(2k

;

2 a2k = 0

T.E. a1

= 4= 1 27 a3 = 4=9 0 14 a5 = 4=25

0 05 : : :

rQD fURXE

1 cos(2k

1)x

f(x) = 2 +

an cos nx = 2

(2k

;1)2

k=1

n=1

;

= 1 57 + 1 27 cos x + 0 14 cos 3x + 0 05 cos 5x + : : :

198

5:	rAZLOVITX FUNKCI@	y = e;	x		ZADANNU@ W INTERWALE		(0 1)
W RQD fURXE PO SINUSAM.
		fUNKCIQ ZADANA NA POLUINTERWALE.
		pRODOLVIM EE NA INTERWAL (;1 0) NE-
		^ETNYM OBRAZOM. tOGDA WSE				KO\FFICI-
		ENTY		an = 0

A KO\FFICIENTY bn			NAHODQTSQ PO FORMULAM, SOOTWETSTWU@]IM SLU-
^A@ NE^ETNOJ FUNKCII W INTERWALE [;l						l ] PRI^EM l = 1:
	2	l		n x	1
bn =		Z	f(x) sin		dx = 2 Z	e;x sin n x dx =
	l			l
		0			0

dANNYJ INTEGRAL QWLQETSQ CIKLI^ESKIM. wOSPOLXZUEMSQ TABLICEJ

Z eax sin bx dx =

eax

(a sin bx ; b cos bx) :

a2 + b2

tOGDA POLU^AEM

2e;x

2e;1

(;sin n x;n cos n x) j0 =

(;sin n ;n cos n );

1 + n2 2

1+n2 2

;

(;sin 0;n cos 0) =

2e;1

[;n (;1)n];

(;n ) =

1+n2 2

1+n2

2e;1

hn (;1)n+1i+

(n ) =

he;1(;1)n+1 +1i :

1+n2 2

rQD fURXE DLQ FUNKCII

f(x) = 1 bn sin n x

= 2

e;1(;1)n+1 + 1

sin n x:

1 + n2 2 i

n=1

z A M E ^ A N I E. oTMETIM, ^TO MOVNO RASKLADYWATX W RQD fURXE FUNKCII, ZADANNYE W PROIZWOLXNOM INTERWALE [a a + 2l] DLINOJ 2l: w \TIH SLU^AQH W FORMULAH NAHOVDENIQ KO\FFICIENTOW RQDA fURXE

(2) NUVNO PREDELY INTEGRIROWANIQ ZAMENITX NA a I a+ 2l: nAIBOLEE ^ASTO \TA SITUACIQ WOZNIKAET, KOGDA FUNKCIQ ZADANA NA INTERWALE [0 2 ] TOGDA PREDELY ; I ZAMENQ@TSQ SOOTWETSTWENNO NA 0 I 2 :

199

6: w INTERWALE (0 2 ) RAZLOVITX W RQD fURXE FUNKCI@ y = x2:

tAK KAK DANNAQ FUNKCIQ NE QWLQETSQ ^ETNOJ ILI NE^ETNOJ, TO NAHODIM WSE KO- \FFICIENTY RQDA.

8 3

8 2

a0 =

f(x) dx =

x2 dx =

3 j0

3 :

;

an = 1

f(x) cos nx dx = 1 Z x2

cos nx dx =

;

U = x2

dV = cos nx dx

1 sin nx

Z x sin nx dx) =

dU = 2x dx V =

= ( n

sin nxj0

; n

;

U = x

dV = sin nx dx

( ; nx cos nxj02 + n1

1 cos nx =

Z cos nx dx) =

dU = dx

V =

sin nx) 2 =

(

x cos nx

(

2 cos 2 n + 0) =

;

; n

bn = 1

U = x2

dV = sin nx dx

x2 sin nx dx =

dU = 2x dx

V =

1 cos nx

cos nx

[

4 2

+ 0] =

= [

; n

x cos nx dx] =

; n

iTAK, RQD fURXE

4 2

f(x) =

an cos nx+ bn sin nx =

+ 4

1 cos nx

1 sin nx

n=1

nAJDEM AMPLITUTU An I FAZU 'n GARMONIK, IME@]IH ODINAKOWU@ ^ASTOTU. iSPOLXZUEM IZWESTNOE IZ FIZIKI PRAWILO SLOVENIQ DWUH GARMONIK

nX=1 an cos nx+bn sin nx= nX=1 An sin(nx+'n) = nX=1 qan2 +bn2 sin(nx+'n):

An = v

+ 16 2

aMPLITUDA n

;

OJ GARMONIKI

1 + 2n2

un4

4=n2

fAZA

'n = arctg bn

= arctg

= ;arctg

;4 =n

200

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2121

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.12.2018280.58 Кб1Теория организации для ТПУ.doc
#
29.05.2015516.61 Кб25Теория экзамен.doc
#
02.05.2019210.94 Кб6теория_«SWOT» анализ_сам.работа.doc
#
12.11.201975.69 Mб0Теория_БЖД_практика.doc
#
30.07.2019118.89 Кб2ТерВер_шпора.docx
#
29.05.20152.54 Mб136Терёхина, Фикс - Высшая математика.pdf
#
22.11.20191.87 Mб7Терминология.doc
#
29.05.201537.45 Кб27Термодин 1-10.docx
#
29.05.201513.16 Кб24Термодин 21-30.docx
#
29.05.201523.55 Кб19Термодин 31-40.doc
#
29.05.2015194.56 Кб17Термодин 71-80.doc