Линию с распределенными параметрами называют неоднородной, если продольные сопротивления в ней различны и поперечные сопротивления неодинаковы.
Когда говорят о линии с распределенными параметрами, то обычно этот термин мысленно связывают с мощными линиями передач электрической энергии на большие расстояния, с телефонными телеграфными воздушными и кабельными линиями, с антеннами в радиотехнике и другими родственными линиями и установками.
Пусть r0 – продольное активное сопротивление единицы длины ли-
нии;
L0 – индуктивность единицы длинны линии; C0 – емкость единицы длины линии; g0 – поперечная проводимость единицы длины линии (она не является обратной величиной продольного сопротивления r0 );
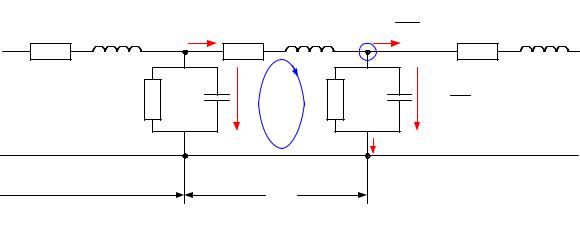
Разобьем линию на участки длиной dx (см. рис. 5.2), x – расстояние, отсчитываемое от начала линии. На длине dx активное сопротивление рано r0dx , индуктивность – L0dx , проводимость утечки – g0dx и емкость – C0dx .
Рис. 5.2
И ток, и напряжение являются в общем случае функциями расстояния вдоль линии x и времени t .
Обойдем, выделенный участок линии по контуру и запишем для него второй закон Кирхгофа - сумма падений напряжения для замкну-
того контура равняется нулю: |
|
∂i + u + |
∂u dx = 0 . |
-u + r dx ×i + L dx |
0 |
0 |
¶t |
¶x |
|
|
Сократив на u и поделив на dx получаем выражение:
- |
∂u = r × i + L |
∂i . |
|
¶x |
0 |
0 |
¶t |
Запишем первый закон Кирхгофа для выделенного узла –1: |
|
i = di + i + |
∂i |
dx |
(1) |
|
|
¶x |
|
Ток di равен сумме токов, проходящих через проводимость g0dx
|
кость C0dx : |
|
|
|
|
|
|
|
|
|
|
¶u |
|
|
¶ |
|
|
¶u |
|
|
di = u + |
|
dx g0dx + |
|
C0dx u + |
|
dx . |
|
¶x |
¶t |
¶x |
|
|
|
|
|
|
|
|
Пренебрегая слагаемыми второго порядка малости, получим |
|
|
|
di = u × g dx + C dx |
∂u |
|
|
|
|
|
|
0 |
|
0 |
¶t |
|
|
|
|
|
|
|
|
|
|
Подставляя (2) в (1) и поделив на dx , после упрощения получаем
- |
¶i |
= g |
|
× u + C |
¶u . |
|
|
|
¶x |
0 |
|
0 ¶t |
Таким образом, получаем систему дифференциальных уравнений в частных производных, которые в математической физике называются
телеграфными уравнениями:
- ¶u¶x- ¶i¶x
= r × i + L |
¶i |
|
0 |
0 |
¶t |
(2а) |
|
× u + C0 ¶u |
= g0 |
|
|
|
¶t |
|
Чтобы решить эти уравнения, воспользуемся символическим мето-
дом
Введем изображения токов и напряжений |
|
i( x, t) ® I ( x)e jωt , u( x, t) ®U ( x)e jωt . |
(3) |
Здесь – I ( x) и U (x) комплексные величины тока и напряжения соответ-
ственно.
Очевидно, что в этом случае мы можем получить следующие соотношения
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶u ® e jωt |
dU ( x) |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶x |
|
|
|
|
dx |
|
L |
∂i ® L I ( x) |
d |
e jωt = jwL I ( x)e jωt |
; |
|
0 |
¶t |
0 |
|
|
|
dx |
0 |
|
|
|
|
|
|
|
|
|
|
¶i |
® e jωt |
d |
I ( x) |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶x |
|
|
|
|
dx |
|
|
C |
∂u ® jwC U (x)e jωt . |
|
|
|
0 ¶t |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив все выше полученные выражения в телеграфные уравнения,
и сократив на множитель e jωt , получим
− |
dU (x) |
|
= (r + jωL |
) I ( x); |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I ( x) |
|
|
|
|
|
|
|
|
|
|
|
|
− |
d |
|
|
= ( g |
|
+ jωC |
|
)U ( x). |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введя обозначения Z0 = r0 + jωL0 , Y0 = g0 + jωC0 ,
мость напряжения и тока от пространственной координаты эти уравнения можно переписать
− |
dU |
= Z I ; |
|
dx |
|
|
|
0 |
|
|
|
|
|
(2в) |
d I |
|
|
|
− |
= Y U. |
|
|
|
|
dx |
0 |
|
|
|
|
|
|
Продифференцируем первое уравнение по x и подставим в него второе получим дифференциальное уравнение второго порядка с постоянными коэффициентами
|
d 2 |
U |
|
= Z Y U → |
d 2U |
− γ2U = 0, γ = |
|
. |
(2г) |
|
|
Z Y |
|
|
|
|
|
|
|
|
dx2 |
0 |
0 |
dx2 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Будем искать решение в виде U = Ae px . Подставляя искомое решение в (2г) получим характеристическое уравнение относительно p
p2 − γ2 = 0 → p1,2 = ±γ .
Теперь решение можно записать в виде
U = A1e p1 x + A2e p2 x = A1e− γx + A2eγx .
Здесь A1, A2 комплексные константы которые определяются с помощью
граничных условий, комплексное число γ = 
 Z0Y0 принято называть
Z0Y0 принято называть
постоянной распространения. Запишем его в алгебраической форме
γ = α + jβ ,
где α – коэффициент затухания (характеризующий затухание падающей волны на единицу длины линии); β – коэффициент фазы (про-
странственная частота); он характеризует изменение фазы падающей
волны на |
единицу |
длины |
линии. |
Размерность величин |
[γ] = [α] = [β] = 1/ км. |
|
|
|
|
|
|
|
|
Найдём ток из уравнений |
|
|
|
|
A e−γx − A eγx |
|
− |
dU |
= Z0 I |
→ I = − |
1 dU |
= |
. |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
Z0 dx |
|
Z0 |
γ |
|
Величину, стоящую в знаменателе Z0  γ называют волновым сопротивлением и обозначают Zв :
γ называют волновым сопротивлением и обозначают Zв :
Z |
|
= |
Z0 |
= |
|
Z0 |
|
= |
|
Z0 |
= z |
e jϕв . |
в |
|
|
|
|
|
|
|
|
γ |
Z0Y0 |
|
|
|
Y0 |
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, ток можно записать |
|
|
|
|
|
I = |
A e− γx − A eγx |
= |
A e− γx |
− |
A e |
γx |
1 |
|
|
|
2 |
|
1 |
|
|
2 |
|
. |
|
|
|
|
Z в |
|
|
|
|
Z в |
|
|
Z в |
Теперь можно перейти от комплексных величин к мгновенным значениям, то есть осуществить обратный переход от комплексных функций к мгновенным значениям тока и напряжения:
I ( x)e jωt → i( x, t), U ( x)e jωt → u(x, t) .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
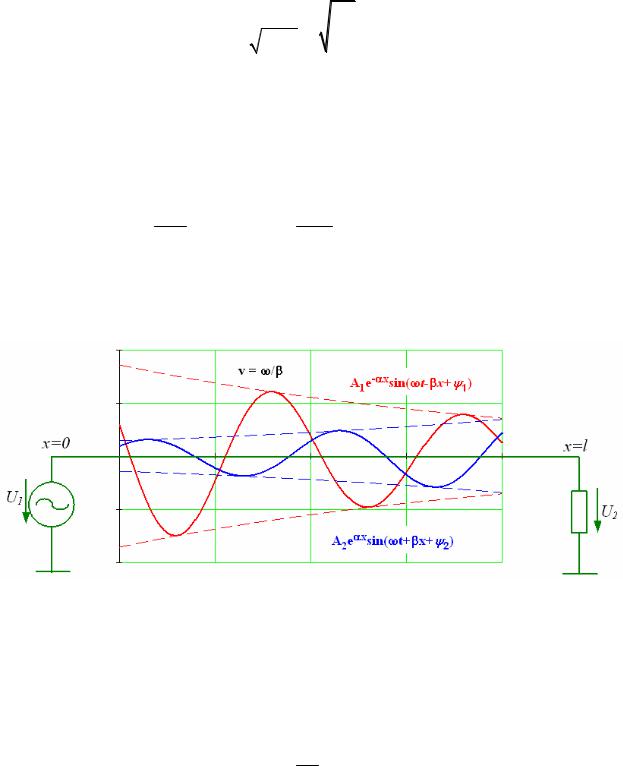
В результате получим |
|
|
|
|
|
|
|
|
|
|
|
|
u( x, t) = A e−αx sin(ωt − βx + ψ ) + A |
eαx sin(ωt + βx + ψ |
2 |
), |
|
|
|
|
|
m1 |
1 |
|
m2 |
|
|
|
|
|
|
|
|
i( x, t) = |
Am1e−αx |
sin(ωt − βx + ψ − ϕ |
|
) − |
Am2 |
eαx sin(ωt + βx + ψ |
2 |
− ϕ |
|
). |
|
в |
|
в |
|
zв |
1 |
|
|
zв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.3
Бегущая волна характеризуется волновыми параметрами – длинной волныλ и фазовой скоростью υ . Скорость распространения – υ и дли-
ну – λ волны можно определить, используя выражения:
ωt − βx + ψ = const → |
d (ωt − βx + ψ1 ) |
= ω − β |
dx |
= 0 → |
υ = |
dx |
= ω , |
|
|
|
1 |
dt |
|
dt |
|
dt β |
|
|
|
λ = 2βπ .
§5.1 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в начале линии
Выпишем комплексное представление волн напряжения и тока вдоль линии, и определим константы интегрирования входящие в эти выражения, используя граничные условия в начале линии:
U = A e− γx + A eγx |
; |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
A1e− γx |
|
A2eγx |
|
|
|
|
|
. |
(4) |
I = |
|
− |
|
|
. |
|
Z в |
Z в |
|
|
|
|
|
|
|
Пусть в начале линии при x = 0 напряжении U1 и I1 , тогда можно получить:
U1 = A1 + A2 ;
I1Zв = A1 − A2 .
Просуммируем первое, и второе уравнения в системе (4), в результате получим выражение для константы A1 :
A1 = U1 + I1 Z в = A1e jψп . 2
Вычитая второе уравнение из первого в системе (4), получим выражение для константы A2 :
A2 = U1 − I1 Z в = Ae jψо . 2
Поставим найденные константы в выражения для напряжения:
|
U |
|
+ I |
|
Z |
|
e− γx + |
U |
|
− I |
|
Z |
|
eγx = |
|
|
eγx + e−γx |
eγx − e− γx |
U = |
|
|
1 |
|
1 |
|
в |
|
|
1 |
|
1 |
|
в |
U |
1 |
|
|
|
− I1 Z в |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Напомним, что в скобках находятся гиперболические функции синус и косинус:

§5.2 Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии
Обозначим расстояние от текущей точки на линии до конца линии y , а длину всей линии ℓ:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ℓ− x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(10) |
Пусть известны напряжения и ток в конце линии U 2 |
и |
|
I 2 . Будем ис- |
пользовать эти значения как граничные условии при |
y = 0 . На основа- |
нии системы уравнений (4) получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U ( y) = A e− γ(ℓ− y ) + A eγ(ℓ− y ) |
|
|
|
|
U (0) = U |
2 |
= A e− γℓ + A eγℓ |
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1e− γ(ℓ− y) |
|
A2eγ(ℓ− y) |
|
|
|
|
|
|
|
A1e− γℓ |
|
|
|
|
A2eγℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. (11) |
I ( y) = |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
I (0) = I |
2 |
|
= |
|
|
|
|
− |
|
|
|
|
|
Z в |
|
|
|
|
Z в |
|
|
|
|
|
Z в |
|
|
|
Z в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решая систему относительно констант A1 и A2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− γℓ |
|
|
|
γℓ |
|
|
|
A = |
|
U |
2 + I 2 Z в |
eγℓ = A e jψп ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= A1e + A2e ; |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
U |
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12) |
|
I Z |
|
= A e− γℓ − A eγℓ, |
|
|
|
|
U1 − I1 Z в − γℓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jψ |
о |
|
|
|
|
|
2 |
в |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
A2 = |
2 |
|
e = |
Ae |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив найденные значения постоянных A1 |
и |
|
A2 |
в систему (4) по- |
лучаем: |
|
|
|
|
( y) = |
|
2ch(γy) + I 2 Z |
вsh(γy); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(13) |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I ( y) = |
|
|
|
sh(γy) + I 2ch(γy), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§5.3 Линии без потерь
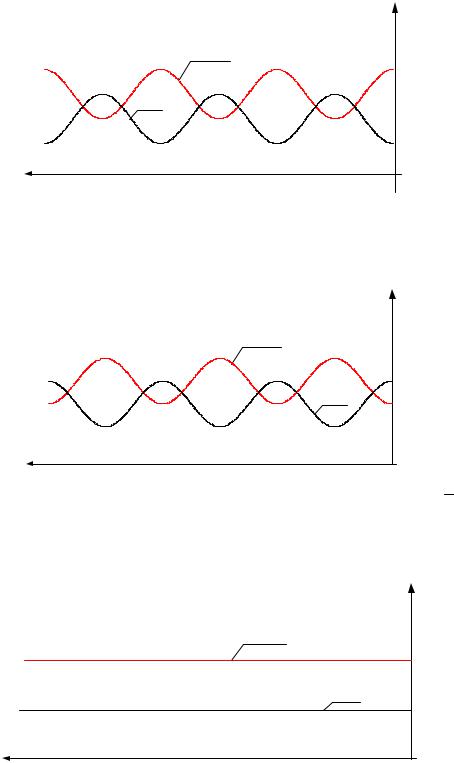
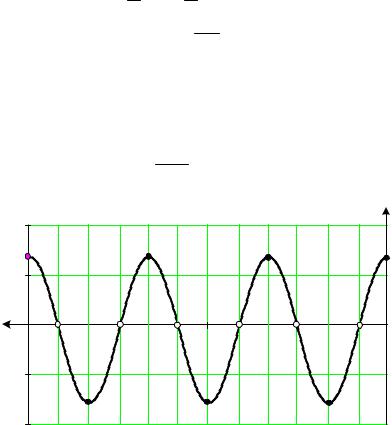
Строго говоря, линии без потерь не существует. Однако можно создать линию с очень малыми потерями (с очень малыми r0 и g0 по сравнению с ω L0 и ω C0 соответственно). В ряде случаев, в особенности при высоких частотах, когда ω L0 >> r0 и ω C0 >> g0 , можно пренебречь наличием потерь в линии и принять r0 = 0 и g0 = 0 . В этом случае коэффициент затухания α = 0 , и коэффициент распространения становится чисто мнимой величиной γ = jβ , β = ω
 L0C0 , а волновое сопротивление явля-
L0C0 , а волновое сопротивление явля-
ется чисто активным:
Для определения напряжения и тока в любой точке линии обратимся к системе уравнений (13)
|
U |
( y) = |
U |
2ch(γy) + I 2 Z вsh(γy); |
|
|
|
U |
|
, |
|
|
|
2 |
|
I ( y) = |
|
|
sh(γy) + I 2ch(γy). |
|
Z в |
|
|
|
|
|
и учтем, что ch(γy) = сh( jβy) = cos(βy), sh(γy) = sh( jβy) =
перепишем уравнения (15):
|
|
|
|
|
|
|
|
|
U |
( y) = |
U |
2 cos(βy) + j I 2 Z в sin(βy); |
|
U |
|
|
|
2 |
|
I ( y) = j |
|
|
sin(βy) + I 2 cos(βy). |
|
|
|
|
Z в |
Используя те же выражения для системы (5) можно записать уравнения линий без потерь через ток и напряжения в начале линии:
|
U |
( y) = |
U |
1 cos(βy) − j I1 Z в sin(βy); |
|
|
|
U |
|
|
(17) |
|
|
1 |
|
I ( y) = − j |
|
sin(βy) + I1 cos(βy). |
|
|
|
|
|
|
Z в |
|
§5.4 Коэффициент отражения
Отношение напряжения отраженной волны в конце линии к напряжению падающей волны в конце линии называют коэффициентом от-
ражения по напряжению и обозначают Ku . В соответствии с формулой (12) можно получить:
|
|
|
|
|
U |
2 |
− I |
2 |
Z |
|
|
|
|
U |
2 |
|
− Z в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A eγl |
|
|
|
|
в |
|
|
|
|
|
|
|
Z − Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
= |
2 |
= |
|
|
|
2 |
|
|
|
|
= |
2 |
|
|
= |
н |
в |
. |
u |
A e−γl |
|
|
|
+ I 2 Z в |
|
|
|
Z + Z |
|
|
|
|
U 2 |
|
|
|
U |
2 |
|
+ Z в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
I 2 |
|
|
|
н |
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из этого выражения видно, что при Z н = Z в |
согласованной нагрузке мы |
получаем Ku = 0 , |
и следовательно |
нет |
отражённой волны, а при |
Z н → ∞ холостом ходе мы получаем |
Ku = 1 то есть волна полностью |
отражается.







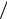 γ называют
γ называют