Introduction to Python for Science, Release 0.9.23

Generalized eigenvalue problem

The scipy.linalg.eig function can also solve the generalized eigenvalue problem

Ax = Bx

where B is a square matrix with the same size as A. Suppose, for example, that we have

In [22]: A = array([[2, 4, 6], [1, -3, -9], [8, 5, -7]]) Out[22]: B = array([[5, 9, 1], [-3, 1, 6], [4, 2, 8]])

Then we can solve the generalized eigenvalue problem by entering B as the optional second argument to scipy.linalg.eig

In [23]: lam, evec = scipy.linalg.eig(A,B)

The solutions are returned in the same fashion as before, as an array lam whose entries are the eigenvalues and a matrix evac whose rows are the eigenvectors.

Hermitian and banded matrices

SciPy has a specialized routine for solving eigenvalue problems for Hermitian (or real symmetric) matrices. The routine for hermitian matrices is scipy.linalg.eigh. It is more efficient (faster and uses less memory) than scipy.linalg.eig. The basic syntax of the two routines is the same, although some of the optional arguments are different. Both routines can solve generalized as well as standard eigenvalue problems.

SciPy also has a specialized routine scipy.linalg.eig_banded for solving eigenvalue problems for real symmetric or complex hermitian banded matrices.

9.3 Solving non-linear equations

SciPy has many different routines for numerically solving non-linear equations or systems of non-linear equations. Here we will introduce only a few of these routines, the ones that

Introduction to Python for Science, Release 0.9.23

are relatively simple and appropriate for the most common types of nonlinear equations.

9.3.1 Single equations of a single variable

Solving a single nonlinear equation is enormously simpler than solving a system of nonlinear equations, so that is where we start. A word of caution: solving non-linear equations can be a tricky business so it is important that you have a good sense of the behavior of the function you are trying to solve. The best way to do this is to plot the function over the domain of interest before trying to find the solutions. This will greatly assist you in finding the solutions you seek and avoiding spurious solutions.

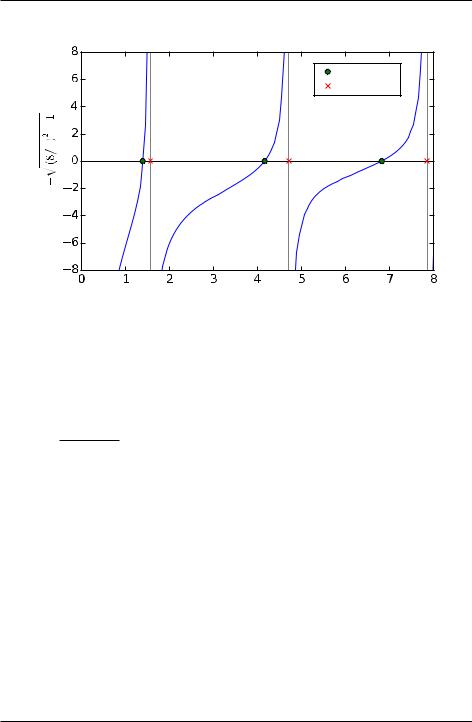
We begin with a concrete example. Suppose we want to find the solutions to the equation

p

tan x = (8=x)2 1

p

Plots of tan x and (8=x)2 1 vs x are shown in the top plot in the figure Crossing functions, albeit with x replaced by . The solutions to this equation are those x values

p

where the two curves tan x and (8=x)2 1 cross each other. The first step towards obtaining a numerical solution is to rewrite the equation to be solved in the form f(x) = 0. Doing so, the above equation becomes

p

tan x (8=x)2 1 = 0

Obviously the two equations above have the same solutions for x. Parenthetically we mention that the problem of finding the solutions to equations of the form f(x) = 0 is often referred to as finding the roots of f(x).

Next, we plot f(x) over the domain of interest, in this case from x = 0 to 8. We are only interested in positive solutions and for x > 8, the equation has no real solutions as the argument of the square root becomes negative. The solutions, the points where f(x) = 0 are indicated by green circles; there are three of them. Another notable feature of the function is that it diverges to 1 at x = f0; =2; 3 =2; 5 =2g.

Brent method

One of the workhorses for finding solutions to a single variable nonlinear equation is the method of Brent, discussed in many texts on numerical methods. SciPy’s implementation of the Brent algorithm is the function scipy.optimize.brentq(f, a, b), which has three required arguments. The first f is the name of the user-defined function

Introduction to Python for Science, Release 0.9.23

true roots false roots

tan

x

Figure 9.2: Roots of a nonlinear function

to be solved. The next two, a and b are the x values that bracket the solution you are looking for. You should choose a and b so that there is only one solutions in the interval between a and b. Brent’s method also requires that f(a) and f(b) have opposite signs; an error message is returned if they do not. Thus to find the three solutions to

p

tan x (8=x)2 1 = 0, we need to run scipy.optimize.brentq(f, a, b) three times using three different values of a and b that bracket each of the three solutions. The program below illustrates the how to use scipy.optimize.brentq

import numpy as np import scipy as sp

import matplotlib.pyplot as plt

def tdl(x): y = 8./x

return np.tan(x) - np.sqrt(y*y-1.0)

# Find true roots

rx1 = sp.optimize.brentq(tdl, 0.5, 0.49*np.pi)

rx2 = sp.optimize.brentq(tdl, 0.51*np.pi, 1.49*np.pi) rx3 = sp.optimize.brentq(tdl, 1.51*np.pi, 2.49*np.pi)

Introduction to Python for Science, Release 0.9.23

rx = np.array([rx1, rx2, rx3]) ry = np.zeros(3)

#print using a list comprehension print(’\nTrue roots:’)

print(’\n’.join(’f({0:0.5f}) = {1:0.2e}’.format(x, tdl(x)) for x in rx))

#Find false roots

rx1f = sp.optimize.brentq(tdl, 0.49*np.pi, 0.51*np.pi) rx2f = sp.optimize.brentq(tdl, 1.49*np.pi, 1.51*np.pi) rx3f = sp.optimize.brentq(tdl, 2.49*np.pi, 2.51*np.pi) rxf = np.array([rx1f, rx2f, rx3f])

#print using a list comprehension print(’\nFalse roots:’)

print(’\n’.join(’f({0:0.5f}) = {1:0.2e}’.format(x, tdl(x)) for x in rxf))

#Plot function and various roots

x = np.linspace(0.7, 8, 128) y = tdl(x)

# Create masked array for plotting

ymask = np.ma.masked_where(np.abs(y)>20., y)

plt.figure(figsize=(6, 4)) plt.plot(x, ymask) plt.axhline(color=’black’)

plt.axvline(x=np.pi/2., color="gray", linestyle=’--’, zorder=-1) plt.axvline(x=3.*np.pi/2., color="gray", linestyle=’--’, zorder=-1) plt.axvline(x=5.*np.pi/2., color="gray", linestyle=’--’, zorder=-1) plt.xlabel(r’$x$’)

plt.ylabel(r’$\tan x - \sqrt{(8/x)^2-1}$’) plt.ylim(-8, 8)

plt.plot(rx, ry, ’og’, ms=5, label=’true roots’)

plt.plot(rxf, ry, ’xr’, ms=5, label=’false roots’) plt.legend(numpoints=1, fontsize=’small’, loc = ’upper right’,

bbox_to_anchor = (0.92, 0.97)) plt.tight_layout()

plt.show()

Running this code generates the following output:

In [1]: run rootbrentq.py

The Brent method finds the three true roots of the equation quickly and accurately when you provide values for the brackets a and b that are valid. However, like many numerical methods for finding roots, the Brent method can produce spurious roots as it does in the above example when a and b bracket singularities like those at x = f =2; 3 =2; 5 =2g. Here we evaluated the function at the purported roots found by brentq to verify that the values of x found were indeed roots. For the true roots, the values of the function were very near zero, to within an acceptable roundoff error of less than 10 13. For the false roots, exceedingly large numbers on the order of 1012 were obtained, indicating a possible problem with these roots. These results, together with the plots, allow you to unambiguously identify the true solutions to this nonlinear function.

The brentq function has a number of optional keyword arguments that you may find useful. One keyword argument causes brentq to return not only the solution but the value of the function evaluated at the solution. Other arguments allow you to specify a tolerance to which the solution is found as well as a few other parameters possibly of interest. Most of the time, you can leave the keyword arguments at their default values. See the brentq entry online on the SciPy web site for more information.

Other methods for solving equations of a single variable

SciPy provides a number of other methods for solving nonlinear equations of a single variable. It has an implementation of the Newton-Raphson method called scipy.optimize.newton. It’s the racecar of such methods; its super fast but less stable that the Brent method. To fully realize its speed, you need to specify not only the function to be solved, but also its first derivative, which is often more trouble than its worth. You can also specify its second derivative, which may further speed up finding the solution. If you do not specify the first or second derivatives, the method uses the secant method, which is usually slower than the Brent method.

Other methods, including the Ridder (scipy.optimize.ridder) and bisection (scipy.optimize.bisect), are also available, although the Brent method is generally superior. SciPy let’s you use your favorite.