Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

PraktykumLAAG

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

3.98 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1814 15 16 17 18 > Следующая >>>

8. Комплексні числа

131

8.7.З’ясувати геометричний зміст співвідношень:

1)		z z0	a;	2)		z z0	a;
3)		z z0	a;	4)	arg z ;

5)	Re z a;			6)	Im z b.

Розв’язання. [2.15.1, 2.17.3, 2.17.4.]

1)Множиною точок, віддаль яких від точки z0 дорівнює a, є коло з центром у точці z0 радіусом a .

2)Нерівність описує внутрішність круга з центром у точці z0 радіусом a .

3)Нерівність описує зовнішність круга з центром у точці z0 радіусом a .

Im z			Im z			Im z
z	0	a		z0	a		z0	a
	0	a			a			a
O		Re z	O		Re z	O		Re z
O		Re z	O		Re z
Рис. до зад. 8.7.1)			Рис. до зад. 8.7.2)			Рис. до зад. 8.7.3)

4)Рівняння задає промінь, що виходить з початку координат під кутом з додатним напрямом дійсної осі.

5)Вертикальна пряма x a.

6)Горизонтальна пряма y b.

8.8. Розв’язати рівняння z3 z 2 0 (z ).

Розв’язання.

[Підбираємо дійсний корінь рівняння. ]

Число z 1 — корінь рівняння.

[Застосовуємо схему Горнера. ]

			1	0		1	2

		1	1	1		2	0
	2							z	1	1,
								z		1,
(z 1)(z		z 2)
(z 1)(z		z 2)			0				2
									2	z	2	0.
							z			z	2	0.

[Розв’язуємо квадратне рівняння.]

132	Модуль 2. ВЕКТОРНА АЛГЕБРА

			z2 z 2 0;
			D 1 8				7;
							2 k

										2 k
7	7(cos i sin )			7	cos				i sin	, k 0, 1;
								2
								2		2
								1 i 7 .
		7 i		7	z	2,3		1 i 7 .
						2,3			2
									2

[Записуємо відповідь.]

z 1, z	2,3	1 i 7 .
1	2,3	2
		2

Коментар. Кубічне рівняння з дійсними коефіцієнтами завжди має принаймні один дійсний корінь, який є дільником вільного члена рівняння.

Або ділимо многочлен z3 z 2 на многочлен (z 1) у стовпчик.

Задачі для аудиторної і домашньої роботи

8.9.Знайдіть дійсні числа x та y з рівняння:

1) (2x y) (x 3y)i 3 i;

2) (x 5y) (x 2y)i 17 8i.

8.10. Знайдіть z1 z2, z1z2, z2 z1, zz1 , якщо z1 2 3i, z2 2 3i.

8.11. Обчисліть:

1) (1 5i)( 2 3i);			2) (1 2i)2;
3)	1 2i	;	4)		4i	.
	1 2i			2	i

8.12. Зобразіть комплексні числа точками комплексної площини:

1)	2 i;	2)	2 i;
3) 3 2i;		4) 2 3i;
5) 1 0i;		6) 0 3i.

8.13.Назвіть комплексне число, спряжене з заданим. Зобразіть задане та спряжене числа точками площини:

1) 1 i;		2)	5;
3)	2i;	4)	2 3i;
5)	5i 4;	6)	0.

8. Комплексні числа

133

8.14. Обчисліть:

;

2) i4 i14 i24 i34 i44 ;

3) i i2

... in,n 4;

4) i i2 i3

i50.

8.15. Запишіть число у тригонометричній і показниковій формах:

1) 1;

2) 1;

3) i;

4) i;

5) 1 i;

6) 1 i;

7) 1 i;

8) 1 i;

10) 1

3 i;

11) cos

i sin ;

12) 1 cos i sin ;

13)sin i cos .

8.16.Обчисліть:

1)5(cos10 i sin 10 ) 2(cos 80 i sin 80 );


										6		6
2)					i sin		6				i sin
2)	2		cos		i sin		6		cos		i sin				;
				7						7
				7		7				7			7
3)		cos140 i sin 140						;			4)			5(cos109 i sin 109 )		.
			cos 50 i sin 50											3(cos 49 i sin 49 )

8.17.Зобразіть на площині множини чисел, модуль та аргумент яких справджують умову:

1)	1,		;	2)	3;
		3
3)	3;			4)	3;
5) 2 3;				6)		;
					4
7) 0		;		8) 0 .
	6

134	Модуль 2. ВЕКТОРНА АЛГЕБРА

8.18. Зобразіть на площині множини чисел, які справджують умову:

Re z 0;

Im 2;

Re z

Im z

z 3 2i

z 1

;

z 1

;

z 1

z i

;

10)

z 1

z i

8.19.Обчисліть: 1) (1 i)25;

	1			20
				20
			3i
3)					;
3)		1 i			;
		1 i

8.20.Знайдіть усі значення коренів:

1)31;

3) 3 4i;

5) 6 1 i ;

3 i

										200
	3				1					200
	3				1
2)							i				;

	2				2
	2				2

	1										24
							3i				24
							3i
4)
4)				1 i							.
				1 i

2) 4			;
2) 4		i	;
4) 3									;
4) 3		2 2i							;

6) 4		1				i		.
6) 4								.
		1 i			3

8.21. Розв’яжіть рівняння у множині комплексних чисел:
1) z2 2z 5 0;						2) 4z2 2z 1 0;
3) z3 6z 9 0;						4) z3 6z 4 0.
8.22. Розв’яжіть систему лінійних рівнянь:
	i)z		(4 2i)z		1 3i,		i)z		(2 i)z		6,
(3	i)z	1	(4 2i)z	2	1 3i,	(2	i)z	1	(2 i)z	2	6,
		1		2				1		2
1)	2i)z1 (2 3i)z2 7;					2)	2i)z1 (3 2i)z2 8.
(4	2i)z1 (2 3i)z2 7;					(3	2i)z1 (3 2i)z2 8.

8.23.Перетворіть на добуток:

1)sin sin 2 sin 3 ... sinn ;

2)cos cos 2 cos 3 ... cosn .

																					8. Комплексні числа																														135
Відповіді
8.9. 1) x 2, y 1; 2)												x 2, y 3.
																											z1		1 2
8.10. z1 z2						2						5,																							6i .
																z2			z1			2	3i,
									2, z1z2
									2, z1z2
																										z2						5
8.11. 1) 17 7i; 2)											3 4i; 3)								3			4 i;	4) 4 8 i.
																				5		5		5					5
8.14. 1) i; 2) 1; 3) 0,											якщо n 4k, i, якщо n 4k 1,																							i 1,						якщо n 4k 2,								1, якщо
n 4k 3;						4) i.

8.15. 1) cos 0 i sin 0; 2)													cos i sin ; 3) cos																i sin					; 4)				cos					i sin						;
8.15. 1) cos 0 i sin 0; 2)													cos i sin ; 3) cos															2	i sin			2		; 4)				cos			2		i sin					2	;
																				3					3											5							5
5)		2 cos				i sin					; 6)			2 cos						3		i sin			3				; 7)		2 cos					5				i sin			5		;
5)		2 cos			4	i sin				4	; 6)			2 cos						4		i sin			4				; 7)		2 cos				4					i sin			4		;
																				2 cos
8)		2 cos 4 i sin										4 ;9)								2 cos				6 i sin 6 ;
				4			4								6							6
10)	cos			3 i sin							; 11)		cos						i sin 7 ;					12)					2 cos			cos							i sin					,	якщо cos						0,
10)	cos			3 i sin				3			; 11)		cos			7			i sin 7 ;					12)					2 cos	2		cos				2			i sin			2		,	якщо cos					2	0,
				cos					i sin									, якщо cos
2 cos																												0; 13)					cos						i sin								.
																										2
			2				2										2									2											2									2
8.16. 1) 10i; 2) 12; 3) i;													4) 5							5		i.
8.16. 1) 10i; 2) 12; 3) i;													4) 5									i.
													6					2		3

8.17. 1) точка M 1; 3 ; 2) коло радіусом 3 з центром у т. O; 3) круг радіусом 3 із центром у

т. O; 4) зовнішні точки круга; 5) кільце без своїх меж; 6) промінь із т. O; 7) кут; 8) верхня відкрита півплощина.

8.18. 1) відкрита півплощина, праворуч від уявної осі;

2) півплощина, розташовану нижче горизонтальної прямої y 2; 3) вертикальна смуга;

4)зовнішність горизонтальної смуги;

5)круг радіусом 1 із центром у т. O;

6)зовнішність круга радіусом 1 із центром у т. 3 2i;

7)уявна вісь;

8)права півплощина;

9)бісектриса 2-ї та 4-ї чверті;

10)півплощина x y 0.

										1
8.19. 1) 212(1 i); 2)										1	( 1		i			3); 3)		29(1 i 3); 4) 212.
8.19. 1) 212(1 i); 2)										2	( 1		i			3); 3)		29(1 i 3); 4) 212.
8.20. 1) cos						2 k	i sin				2 k		, k 0,1, 2; 2)						cos 1 4k i sin								1 4k	, k
						2 k					2 k																1 4k		0, 3;
											3																8		0, 3;
					3						3									8							8
3) 2 i, 2 i; 4)													8k 3				i sin			8k 3				,	k 0,1, 2;
3) 2 i, 2 i; 4)									2 cos								i sin							,	k 0,1, 2;
															12					12
															12					12
		1			24k 19										24k 19
		1			24k 19										24k 19
5)				cos				i sin										,		k 0, 5;
	12
	12
			2		72										72
	1				13 24k										13 24k
	1				13 24k										13 24k

6) 8								i sin												k 0, 3.
6) 8		2		cos	48			i sin							48			,		k 0, 3.
		2			48										48
								1						i; 3)		3, 3 i						; 4)
8.21. 1) 1 2i; 2)												3									3		2, 1
												3														3.
								4																		3.
								4			4							2

136

Модуль 2. ВЕКТОРНА АЛГЕБРА

8.22. 1)

z1 1, z2

i; 2) z1

2 i,

z2 2 i.

sin

(n 1)

sin

cos

(n 1)

8.23. 1)

; 2)

sin

Модуль 3. АНАЛІТИЧНА ГЕОМЕТРІЯ

9. Геометрія прямої і площини

Навчальні задачі

9.1. Задано пряму L :	x 1	y 2	z 4	. Знайти координати напрямно-
	2	3	5

го вектора s і точку M0, що належить прямій.

Розв’язання. [3.4.1, 3.4.4.]

Задані рівняння є канонічними рівняннями прямої. Отже, числа, що стоять у знаменниках дробів — це координати напрямного вектора прямої

	2
	2


	3
s	3	.


5

Точка, через яку проходить пряма, має координати M0(1;2; 4).

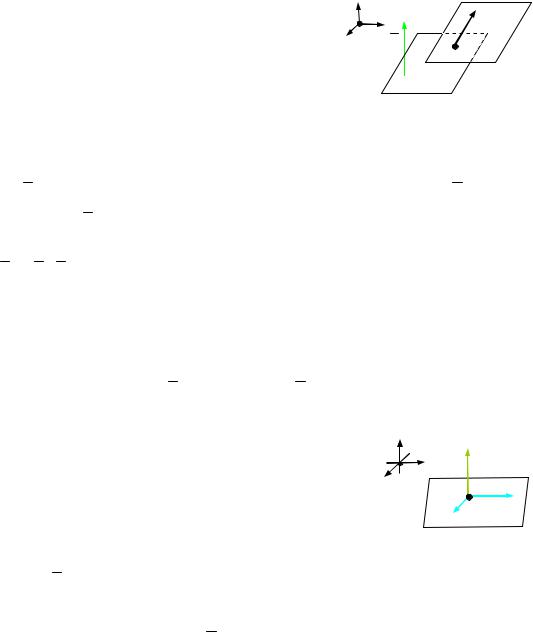
9.2.Записати канонічні й параметричні рівняння прямої L, що проходить через точку M0(1; 1;0) паралельно вектору a ( 2;5; 6)T .

Розв’язання. [3.4.1., 3.4.3, 3.4.4.] 

Оскільки вектор

ненульовий,

то його можна взяти за на-

прямний вектор шуканої прямої.

Нехай точка M(x;y;z) L. належить прямій L.

Рис. до зад. 9.2

[Підставляючи координати точки M0

і координати вектора

в канонічні

[3.4.4] і параметричні [3.4.3] рівняння, дістаємо:]

Канонічні рівняння прямої

L :

x 1 y 1

;

Параметричні рівняння прямої

1 2t,

L :

1 5t, t .

6t,

Коментар.Стислий загальний розв’язок задачі:

0 a

s (L),

L a

L : r r0 a

L(M0 ;a )

M(r )

L : r r0 ta,t .

138	Модуль 3. АНАЛІТИЧНА ГЕОМЕТРІЯ

9.3.Записати канонічні й параметричні рівняння прямої L, яка проходить

через точки M1(3;3;3), M2(4;5;6).

Розв’язання. [3.4.6.]

Нехай точка M(x;y;z) L. Тоді [підставляючи у формулу [3.4.6] координати

точок M1 та M2 дістаємо]
канонічні рівняння прямої
	L : x 3 y 3					z 3		;
1				2			3
[підставляючи координати точки M1					і напрямного вектора s (L) (1;2; 3)T
дістаємо]
параметричні рівняння прямої
			3	t,
		x	3	t,

			3	2t,		t .
	L : y		3	2t,		t .

			3	3t,
		z	3	3t,

Коментар. Напрямним вектором шуканої прямої L є ненульовий вектор
						1
						1



						2
M1M2 r2 r1						2	s(L).

						3
						3

Для знаходження канонічних і параметричних рівнянь використано умову колі-

неарності векторів M1M і M1M2.

9.4.Записати рівняння прямої L, яка проходить через точку M0(7; 3;1) па-

ралельно прямій L	:		x	y 7	z 1 .
ралельно прямій L	:	2		y 7	z 1 .
1		2		3	0
Розв’язання. [3.4.4.]

З рівняння прямої L1 випливає, що напрямний вектор

	2
	2


	3
s1(L1)	3	.


0

L1 s1

L M0 M

Рис. до зад. 9.4

Оскільки пряма L паралельна прямій L1, то за її напрямний вектор можна взя-

ти напрямний вектор прямої L1 :

	2
	2


	3
s(L) s1(L1)	3	.


0

				9. Геометрія прямої і площини							139
Нехай точка M(		) L. Тоді (див. зад. 9.2)
Нехай точка M(	r	) L. Тоді (див. зад. 9.2)
				7					2
			x	7					2	[3.4.4]


		r r		3					3
		r r	y	3	колінеарний s				3
0							1


			z	1				0

канонічне рівняння прямої
			L :	x 7		y 3 z 1 .
				2		3		0
9.5. Знайти нормальний вектор площини 3x 2y 5z 1											0.
Розв’язання. [3.3.2.]
Задане рівняння є загальним рівнянням площини.
Нормальний вектор площини
							

						3



					n 2		.


						5

Коментар. Коефіцієнти при змінних у загальному рівнянні є координатами нормального вектора цієї площини. Нормальний вектором площини буде і будь-який вектор n, 0.

9.6.Записати рівняння площини P, що проходить через точку M0(1; 3;2)

перпендикулярно до вектора

(4;0;5)T .

Розв’язання. [3.3.3] 

Оскільки вектор

перпендикулярний до площини P,

то

його можна взяти за нормальний вектор площини

P :

(P)

Нехай точка M(

) M(x;y;z) P. Тоді

Рис. до зад. 9.6

[підставляючи у рівняння [3.3.3] координати точки M0

і вектора

, дістаємо]

4(x 1) 0(y 3) 5(z 2) 0

P : 4x 5z 14 0.

шукане рівнянняплощини

Коментар. Стислий загальний розв’язок задачі:

P a 0 a n(P);

M(r ) P(M0;a ) r r0 a

P : (r r0,a ) 0.

140	Модуль 3. АНАЛІТИЧНА ГЕОМЕТРІЯ

9.7.Записати рівняння площини P, яка проходить через точку M0(2; 1;1)

паралельно площині P1 : x 4y 5z 1 0 .

Розв’язання. [3.3.2, 3.3.3.]

Оскільки площина P P1, то за нормальний вектор площини P можна взяти нормальний вектор площини P1 :

		1
		1



n(P) n1(P1) 4			.


	5

M P

Рис. до зад. 9.7

Нехай точка M(r ) P. Площину P, що проходить через точку M0(r0 ) перпе-

ндикулярно до вектора n1 задає рівняння (див. зад. 9.6)

3.3.3

(r r0,n1) 0 1(x 2) 4(y 1) 5(z 1) 0.

Рівняння шуканої площини

P: x 4y 5z 11 0.

9.8Записати рівняння площини P, яка проходить через точку M0(2;0; 5), паралельно двом векторам u (1;2;0)T та v (0; 1;3)T .

Розв’язання. [3.3.1, 3.3.4.] 

Вектори u та v — не колінеарні, бо 1

3 .

Нехай точка

M(r ) M(x;y;z) P.

Рис. до зад. 9.8

Оскільки точка M0(r0 ) M0(2;0; 5)

		2
	x	2		1


r r0					2
r r0	y		,u		2	,v


	z	5		0

P, то вектори

	0
	0

	1	— компланарні
	1	— компланарні


3

[2.12.3]							x 2	y	z 5	[1.7.2]
(				,		) 0	1	2	0	0
(	r	r0,	u	,	v	) 0	1	2	0	0
	мішаний добуток						0	1	3

(x 2) 6 y 3 (z 5) ( 1) 0; P : 6x 3y z 17 0.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1814 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.03.2016931.53 Кб4Poyasnyuvalna_zapiska_moya.docx
#
10.11.2018687.1 Кб6praktichni_roboti_po_visual_basic.doc
#
12.05.20153.46 Mб60Praktikum2_TBиМС.doc
#
12.05.20153.41 Mб13PraktykumD+ICh.pdf
#
12.05.20154.04 Mб26PraktykumLA+AG.pdf
#
12.05.20153.98 Mб47PraktykumLAAG.pdf
#
17.03.20163.49 Mб20PraktykumRiady.pdf
#
19.11.2018693.25 Кб9Prakt_BZhD_2011_2012.doc
#
23.11.2019120.32 Кб1prakt_rab_po_tekhnologiam.doc
#
17.11.20184.35 Mб2Prakt_rab_Shlaki_16.doc
#
17.03.20165.28 Mб10Processing 2 Creative Coding Hotshot.pdf