7.2 Физическая природа стохастических индикаторов.

Физический смысл этих свойств стохастических индикаторов заключается в следующем. Если переменная случайна, то в предикатеконстантаопределяет границу детерминированного множества, при попадании в которое случайной величиныиндикаторыипринимают значение 1. В этом случае достоверность событийиравна 1.

В дважды неопределенном предикате переменнаяопределяет границу “неопределённого” (“случайного”) множества, при попадании в которое случайной величиныиндикаторы могут принимать уже любые значения на интервале (0,1]. Это объясняется тем, что в данном случае как размеры, так и расположение множестваи вероятность попадания случайной величины в такое множество будет также случайной.

При этом вероятность представляет собой функцию распределения случайной величины

а вероятность предиката будет уже представлять собой функцию случайного аргумента – случайный индикатор, поэтому

(7.17)

Причём левая часть выражения (7.17) представляет собой число – математическое ожидание индикатора , а правая часть – случайную величину – функцию случайного аргумента- индикатор[7,12].

Кроме того, понятие стохастического индикатора может быть получено непосредственно из вероятности , которая, в действительности, является случайной величиной, поскольку она зависит только от случайных величини. Следовательно, она является случайным индикаторомэтого события

. (7.18)

То же самое можно сказать и о вероятности , следовательно,

При известных функциях распределения ислучайных величиниматематические ожиданияис учетом (7.16) определяются следующим образом

(7.19)

Таким образом, математические ожидания истохастических индикаторов совпадают со значениями вероятностей (7.11) и (7.12), полученных на основе классических методов. Это означает, что классические методы позволяют определить только одну числовую характеристику вероятностей (7.11), (7.12). В то время как методы теории стохастической индикации являются более информативными и позволяют получить функции распределения случайных величини, которые полностью характеризуют указанные случайные величины и позволяют получить гарантированные значения вероятностейи.

При этом переменные, находящиеся в левых частях предикатов иявляются управляющими переменными, а соответствующие им переменные в правых частях называются управляемыми переменными.

Например, при испытаниях и эксплуатации управляющей (трансформирующей) переменной является нагрузка , а сопротивляемостьявляется управляемой (трансформируемой) переменной. С другой стороны, на этапе проектирования сопротивляемостьявляется управляющей (трансформирующей) переменной, а– управляемой переменной. Так, в предикатах (2.45) и (2.46), левая часть является управляющей, а правая – управляемой.

7.3 Методы определения показателей надежности на основе методов стохастической индикации.

Всё оказанное выше позволяет подойти к методам определения функций распределения индикаторов ипри условии независимости случайных величин и. Для решения этой задачи сформулированы теоремы о функциях распределения стохастических индикаторов [11,12].

Теорема Т1. Если функции распределенияинезависимых случайных величиниизвестны, то

( 7.20)

Доказательство.Cучетом (7.13) введём обозначения:

Тогда, поскольку функция неубывающая, то

_{что и требовалось доказать.}

Теорема Т2. Если дополнительные функции распределенияислучайных величиниизвестны, то

(7.21)

Доказательство.Cучетом (7.14) введём обозначения:

Тогда, поскольку функция невозрастающая¹, то

что и требовалось доказать.

Пример 1. Пусть случайные величины иобе подчинены показательным законам распределения с параметрамиисоответственно:

, (7.22)

.

Тогда согласно Т1 ( 7.20) имеем

(7.23)

(7.24)

откуда

, (7.25)

(7.26)

Из (7.24) может быть получено гарантированное значение вероятности безотказной работы объекта, откуда следует

,

откуда следует

. (7.27)

Формула (7.26) представляет собой математическое ожидание вероятности безотказной работы объекта. Тогда математическое ожидание вероятности отказа объекта составит

(7.28)

Полученное на основе методов теории стохастической индикации выражение (7.28) для вероятности безотказной работы совпадает с её выражением (см. таблицу 3.1), полученным известными методами [2-5,16,18].

Пример 2. Пусть случайные величины ираспределены нормально и имеют соответственно числовые характеристикиито есть

(7.29)

(7.30)

где (.) – нормированная пофункция нормального распределения (табличная функция) [2,5,18,19,22].

Тогда согласно теореме Т1 (7.20) и соотношениям (7.29), (7.30)

(7.31)

где

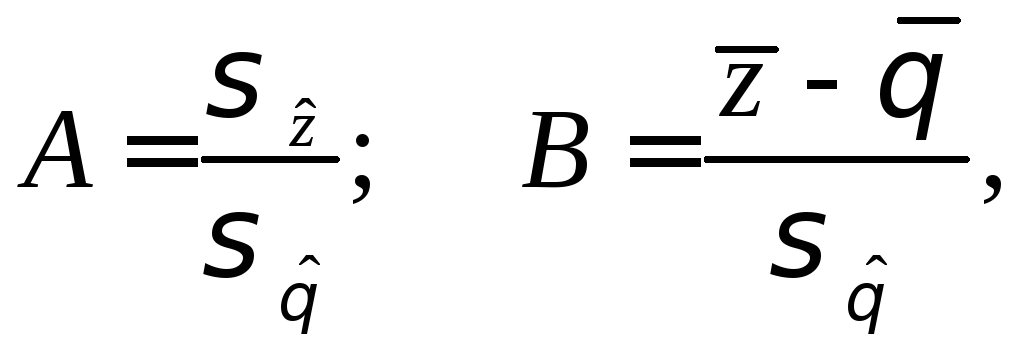
откуда

(7.32)

. (7.33)

Однако в большинстве случаев вычисление показателей а также соответственно показателейв аналитической форме затруднительно и не всегда возможно. В этом случае для вычисления данных показателей предлагается графоаналитический метод, представленный на рис.7.3.